Слайд 2
Без игры не может быть полноценного умственного развития.
Игра-это огромное светлое окно, через которое в духовный мир
ребёнка вливается живительный поток представлений, понятий. Игра-это искра, зажигающая огонёк пытливости и любознательности.
В.А.Сухомлинский
Слайд 3
Основная цель – активизация познавательной деятельности учащихся на
уроках математики, развитие любознательности и глубокого познавательного интереса к
предмету через игровую деятельность.
Слайд 4
Актуальность применения игровых технологий на уроках математики:
игровые формы

обучения на уроках создают возможности эффективной организации взаимодействия педагога
и учащихся, с элементами соревнования, непосредственности, неподдельного интереса;
в игре заложены воспитательные и образовательные возможности;
в процессе игр дети приобретают самые различные знания о предметах и явлениях окружающего мира;
игра развивает детскую наблюдательность и способность определять свойства предметов, выявлять их существенные признаки;
игры очень хорошо уживаются с “серьезным” учением;
включение в урок игр и игровых моментов делает процесс обучения интересным и занимательным, создает у детей бодрое рабочее настроение, облегчает преодоление трудностей в усвоении учебного материала;
разнообразные игровые действия, при помощи которых решается та или иная умственная задача, поддерживают и усиливают интерес детей к учебному предмету.
игры оказывают большое влияние на умственное развитие детей, совершенствуя их мышление, внимание, творческое воображение.
Слайд 5
Игровые технологии способствуют достижению следующих целей:
активизации мыслительной деятельности,
развитию познавательных способностей;
развитию логического мышления;
углублению знаний по математике;
восприятию межпредметных
связей;
привитию математической культуры;
сплочению коллектива, формированию деловых взаимоотношений;
развитию индивидуальности и коммуникативных способностей.
Слайд 6
Требования к организации игры на уроке.
Игра должна быть
построена на интересе.
Игра должна основываться на свободном творчестве и
самостоятельной деятельности учащихся.
Игра должна быть доступной для учащихся данного возраста, цель игры – достижимой, а оформление – красочным и разнообразным.
Математическая сторона содержания игры всегда должна отчетливо выдвигаться на первый план. Только тогда игра будет выполнять свою роль в математическом развитии детей и воспитании интереса к предмету.
Слайд 7
Нетрадиционные формы, методы
и средства
обучения.
Дидактические
игры
Экскурсы
в историю
предмета
Практикумы
Нестандартные
уроки
Интеграция
учебных
предметов
Слайд 8
Беленкова Е.Ю. и Лебединцева Е.А. «Задания для обучения
и развития учащихся»,
Попова А.А. «Поурочные разработки к учебнику
Н.Я.Виленкина».
Коваленко В.Г. Дидактические игры на уроках математики.
Новые горизонты открывает применение ИКТ на уроках математики.
Методическая литература в помощь учителю:
Слайд 9
,
,,
С=З
Отрезок
В начале урока можно предложить учащимся, разгадав ребус
или кроссворд, самим назвать тему занятия.
Слайд 12
Ж=Г
,,
1,2,4
1
В
Н=Г
М х 2
Ы
Круговые диаграммы
Слайд 13
1. Часть прямой, ограниченная двумя точками.
2. Это есть
у слова, растения и уравнения.
3. Равенство, содержащее неизвестное число,
обозначенное буквой.
4. Компонент действия вычитания, который находят сложением.
5. Решение задач способом составления уравнений.
1
2
4
3
5
у
У
29 + x = 45
О
Y – 37 = 18 Е
90 – y = 62 И
31 + y =16 + 44 Ж
80 – с =21 + 19 Н
40 – 3 = с + 13 М
18
24
40
16
29
55
40
28
55
У
М
Н
О
Ж
Е
Н
И
Е
Слайд 15
Уроки-игры (КВН, урок-путешествие, урок-экскурсия), использование игровых
ситуаций на уроках («Магические квадраты», «Индивидуальное лото», «Кто быстрее»,
«Cтрела» и др.), отгадывание ребусов, кроссвордов, решение занимательных задач, Устные разминки, занимают немного времени, развивают быстроту реакции, внимательность, умение четко и конкретно мыслить.
Примеры использования элементов игровых технологий в системе работы с учащимися 5 - 7 классов.
Слайд 16
УСТАНОВИТЕ ЗАКОНОМЕРНОСТЬ И НАЗОВИТЕ ЧИСЛО, КОТОРОЕ СЛЕДУЕТ ВПИСАТЬ
В ПУСТУЮ КЛЕТКУ.
Слайд 19
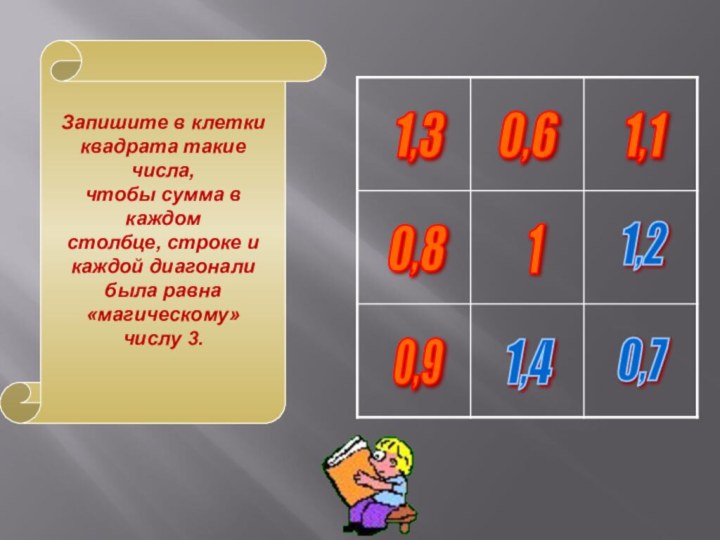
Запишите в клетки
квадрата такие числа,
чтобы сумма в каждом
столбце,
строке и
каждой диагонали
была равна
«магическому»
числу 3.
1,2
0,7
1,4
0,9
1,1
1
0,8
1,3
0,6
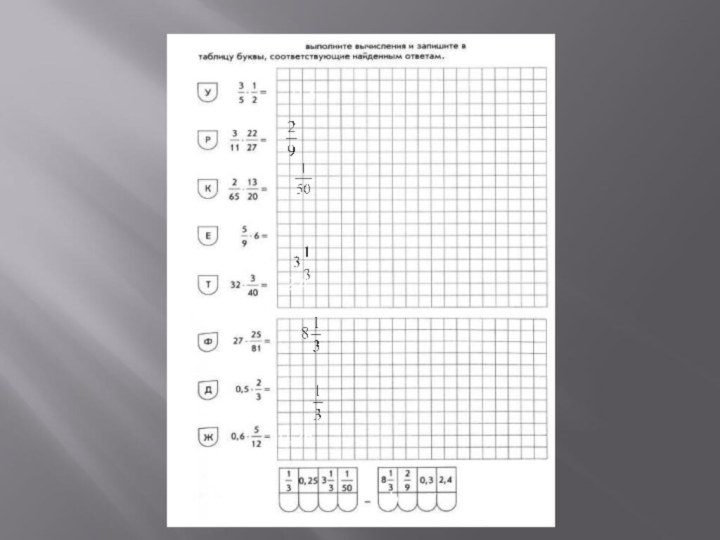
ученики получают по одной большой карточке, разделенной на квадратики
с ответами (числами) и буквами, а также маленькие квадратики.
Выполняя упражнения, ученики закрывают маленькими квадратиками на большой карточке те числа, которые совпадают с ответами решенных примеров.
При верных вычислениях после выполнения всех основных упражнений из всех чисел на карточке часть будет закрыта, а из оставшихся надо сложить слово. Можно сразу просмотреть и указать ошибки, выставить оценки.
Индивидуальное лото.
Слайд 21
296
С
513
З
1000
М
499
Н
877
П
630
У
45
О
555
Т
40
М
8
Е
90
Ь
4
А
7
Р
57
И
96
Е
14
Р
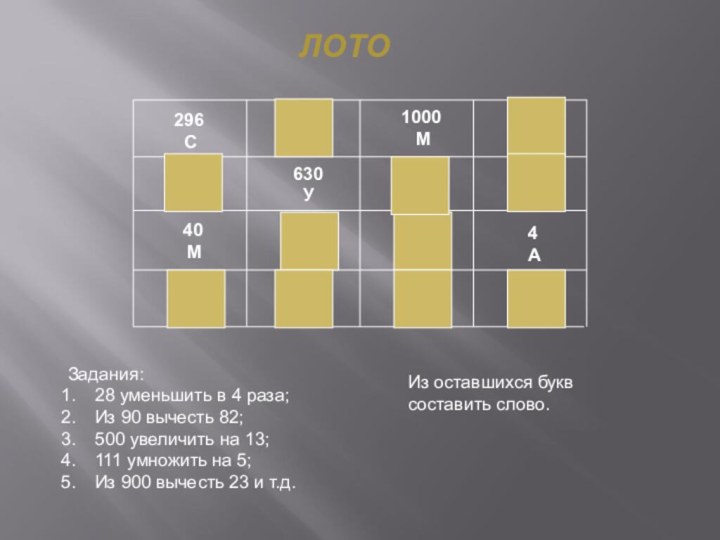
ЛОТО
Задания:
28 уменьшить
в 4 раза;
Из 90 вычесть 82;
500 увеличить на 13;
111 умножить на 5;
Из 900 вычесть 23 и т.д.
Из оставшихся букв
составить слово.
Слайд 22
При отработке навыков выполнения действий с десятичными дробями
в 5 классе провожу математическую эстафету «Заполни клетку», каждая
команда (ряд) получают листочки. Учащиеся по очереди выполняют действия. Ответ предыдущего действия ставится в первую клетку следующего.
Выигрывает та команда, которая первой скажет правильный ответ в последней клетке.
Слайд 24
В 6 классе для отработки навыков построения точек
на координатной плоскости по их координатам использую «Конкурс художников».
Даны
координаты точек (3;14); (4;15); (3;16); (2;15); (3;14); (0;7);(1;6); (-2;3); (-4;3);
(-2;2); (-1;1); (0;2); (1;1); (2;2); (3;2); (4;2); (5;1); (6;2); (3;5); (0;2); (0;0); (1;-1); (1;-3); (2;-4);
(2;-7); (0:7); (0;-8); (1;-9); (3;-7); (5;-9); (6;-8); (6;-7); (4;-7); (4;-4); (5;-3); (5;-1); (6;0); (6;2); (7;1); (8;2); (10;3); (8;3);(5;6);(6;7);(3;14);
Глаза (1;8);(2;9);(3;8);(4;9);(5;8);
Рот (1;7); (2;6);(4;6);(5;7);(1;7).
Что получилось?
Слайд 26
Большой интерес вызывают задания, которые позволяют
узнавать интересные факты из других областей знаний, получая эту
информацию посредством математики и расширяя таким образом кругозор.
Слайд 27
2
3
а
3
5
м
и
4
5
л
3
7
л
3
7
я
2
9
р
4
7
и
4
5
я
2
9
мамиллярия
Слайд 28
Род кактусов Маммиллярия - небольшие кактусы шаровидной или
укороченно-цилиндрической формы. Стебель одиночный или дающий отростки.
Цветки
у большинства видов некрупные, расположены в виде венка на верхушке, часто в 2-3 круга. Плоды сочные, ягодообразные, погружены в мякоть стебля и выходят наружу после созревания, обычно на второй год.
Мамиллярия
Слайд 30
СЕКВОЙЯ
Замечательна секвойя тем, что является самым высоким деревом
в мире. Секвойя высотой в 60 метров (два десятиэтажных
дома, поставленных друг на друга) – обычное дело. Но экземпляры выше 90 метров – тоже не редкость.
Слайд 32
Хлебное дерево (джек-фрут) – родное для западных островов
Тихого океана.
Хлебное дерево вырастает примерно до 20-26 метров в
высоту, листья его большие и толстые. Но не за рост его уважают.
Слайд 33
Эти плоды являются основным продуктом питания
для жителей тропических островов, где растут хлебные деревья. Плоды
едят и жареными, и печёными, и варёными. На вкус эта еда – что-то среднее между картошкой и хлебом.
Но не хлебом единым жив человек! Из хлебного дерева также делают лодки, ведь древесина его лёгкая и прочная, к тому же чрезвычайно устойчива к термитам.
Слайд 34
Артокарпус – научное название хлебного дерева.
Продолговатые плоды артокарпуса
поражают своими размерами.
Найдите значения выражений и узнайте эти размеры.
Масса
плодов (кг):
36
Слайд 35
Длина плодов (см):
90
Диаметр плодов (см):
50
Слайд 36
Большой интерес учащихся вызывают задания, содержащие
малоизвестные, интересные факты о природе родного края, о редких
животных России.
Слайд 37
На большей части территории России, вплоть до
бассейна реки Колымы и Забайкалья, гнездуется серый журавль.
Синевато-серое
оперение большей части тела позволяет птице маскироваться от врагов среди лесистой местности. Эта красивая крупная птица имеет высоту около 115 см, размах крыльев 180—200 см.
А вот вес серого журавля вы узнаете из «Геометрического лабиринта».