Слайд 2
оглавление
1 – титульный лист
2 – оглавление
3 –Скрещивающиеся прямые
4
– теория
5 – пример
6 – теорема 1
7 – теорема
2
8 – пересекающиеся прямые
9 – свойства
10 - Перпендикуляр и наклонная
Слайд 3
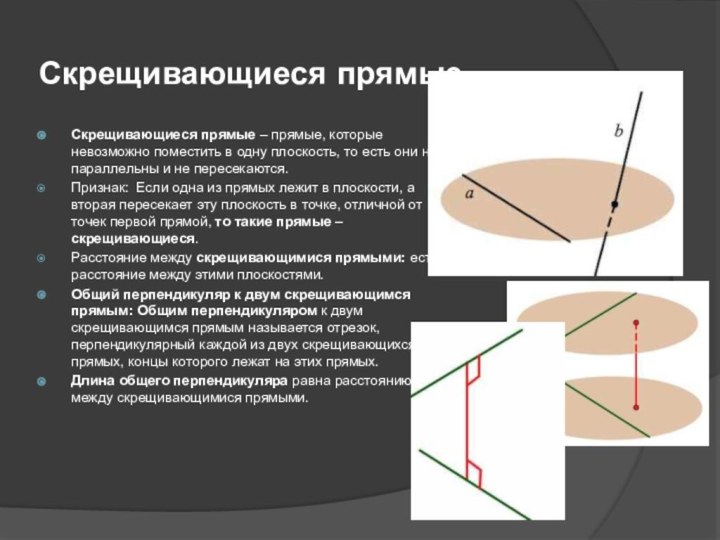
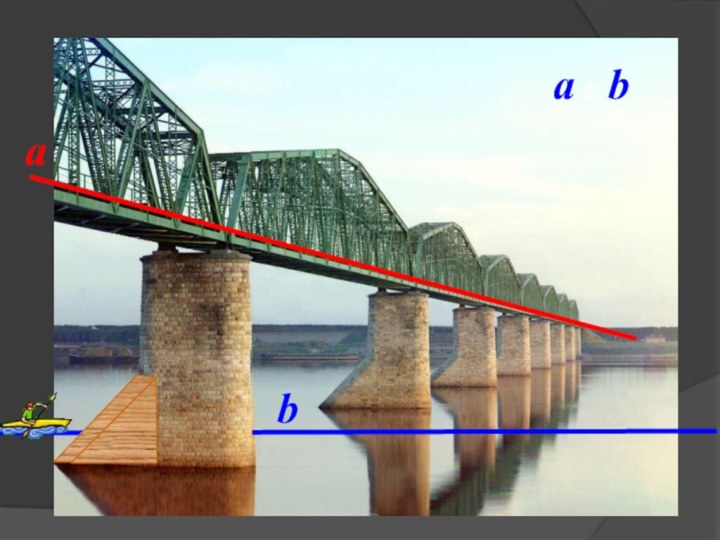
Скрещивающиеся прямые
Скрещивающиеся прямые – прямые, которые невозможно поместить в
одну плоскость, то есть они не параллельны и не
пересекаются.
Признак: Если одна из прямых лежит в плоскости, а вторая пересекает эту плоскость в точке, отличной от точек первой прямой, то такие прямые – скрещивающиеся.
Расстояние между скрещивающимися прямыми: есть расстояние между этими плоскостями.
Общий перпендикуляр к двум скрещивающимся прямым: Общим перпендикуляром к двум скрещивающимся прямым называется отрезок, перпендикулярный каждой из двух скрещивающихся прямых, концы которого лежат на этих прямых.
Длина общего перпендикуляра равна расстоянию между скрещивающимися прямыми.
Слайд 4
Угол между скрещивающимися прямыми: Углом между двумя скрещивающимися
прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным
скрещивающимся прямым.
(Одну из прямых можно вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).
Слайд 6
Теорема 1(признак скрещивающихся прямых)
Если одна из двух прямых
лежит в некоторой плоскости, а другая прямая пересекает эту
плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.
Доказательство
Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.
Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость - α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана.
Слайд 7
Теорема 2
Теорема 2.
Через каждую из двух скрещивающихся прямых

проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство.
Пусть
нам даны две скрещивающиеся прямые АВ и CD. Докажем, что через прямую АВ проходит плоскость, параллельная прямой CD, и притом только одна.
Проведем через точку А прямую АЕ, параллельную прямой DC (Рис. 6.). По теореме о параллельных прямых, такая прямая существует и единственная. Тогда через две пересекающиеся прямые АВ и АЕ можно провести единственную плоскость α.Так как прямая DC, которая не лежит в плоскости α, параллельна прямой АЕ, лежащей в плоскости α, значит, что прямая DCпараллельна плоскости α, по признаку параллельности прямой и плоскости. Существование доказано.
Докажем единственность такой плоскости. Пусть существует другая плоскость β, которая проходит через прямую АВ и параллельна прямой DC. Тогда прямая АЕ пересекает плоскость β, а значит и параллельная ей прямая DC пересекает плоскость β, по лемме. То есть, прямая DC не параллельна плоскости β. Получили противоречие. Следовательно, плоскость α –единственная. Теорема доказана.
Слайд 8
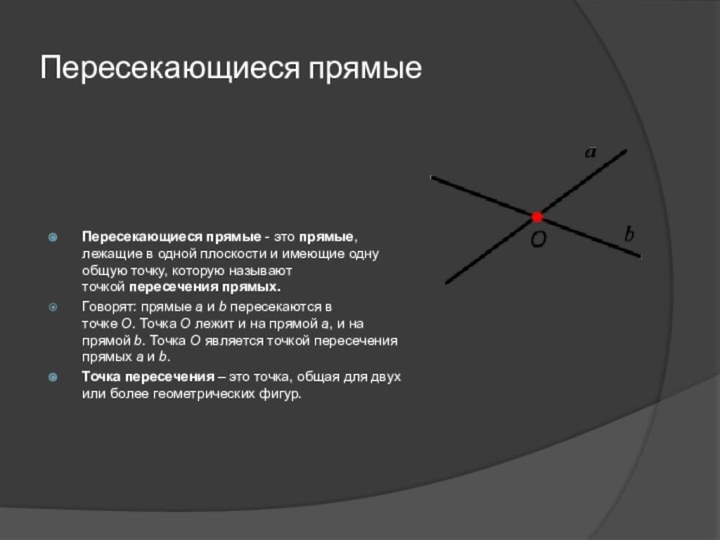
Пересекающиеся прямые
Пересекающиеся прямые - это прямые, лежащие в одной плоскости и
имеющие одну общую точку, которую называют точкой пересечения прямых.
Говорят: прямые a и b пересекаются в точке O. Точка O лежит
и на прямой a, и на прямой b. Точка O является точкой пересечения прямых a и b.
Точка пересечения – это точка, общая для двух или более геометрических фигур.
Слайд 9
Свойства
Свойства: Пересекающиеся прямые 1. ∠3 и∠4 – смежные
∠1 и ∠2 – смежные ∠3 + ∠4 =
180° ∠1 + ∠2 = 180° 2. ∠1 и ∠3 – вертикальные ∠2 и ∠4 - вертикальные ∠1 = ∠3 ∠2 =∠4 a b 3 1 2 4 При пересечении двух прямых образуются две пары углов – вертикальные и смежные. Вертикальные углы равны.