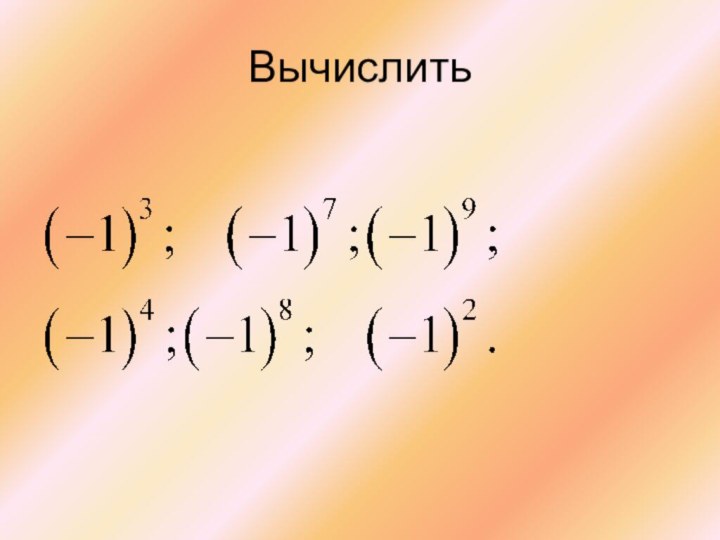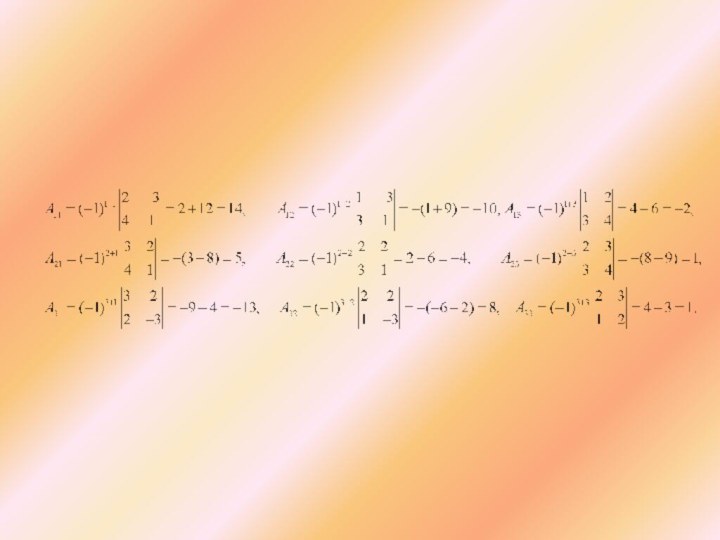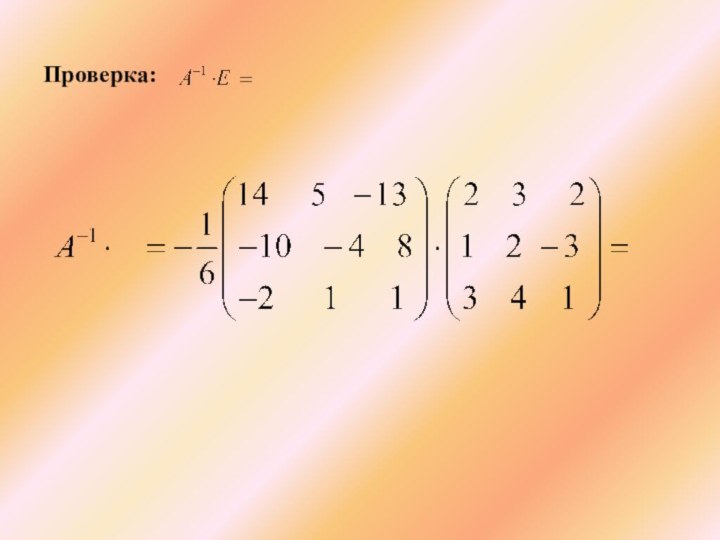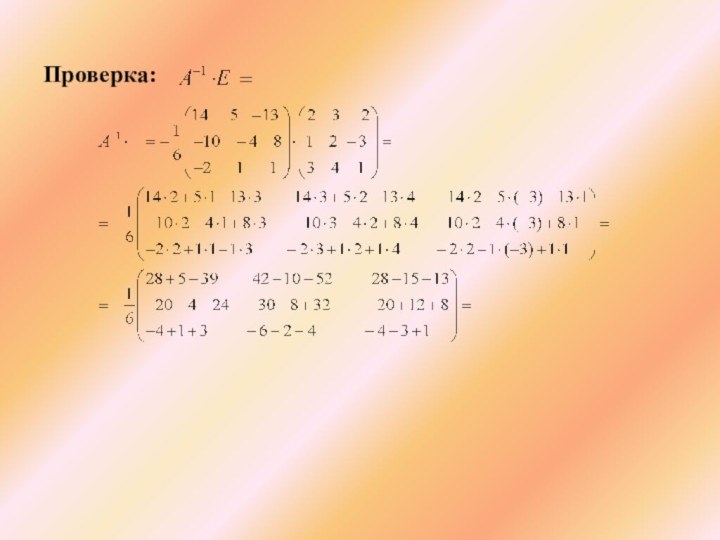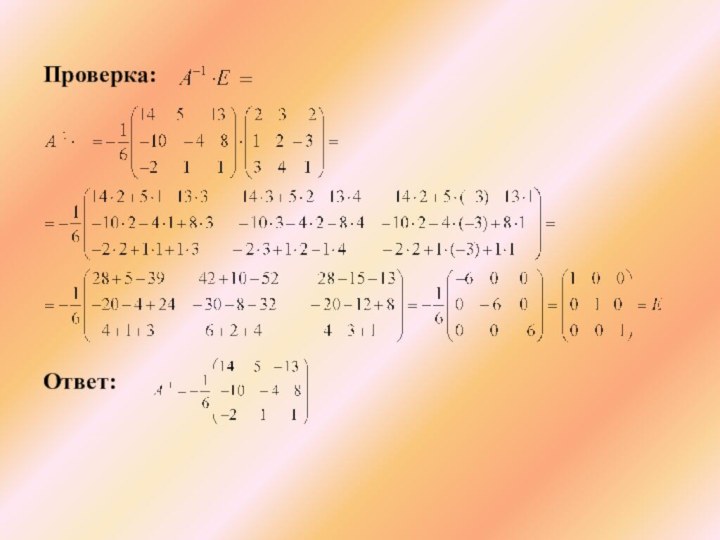Слайд 3
Цели занятия:
сформировать:
- понятие о матрицах, их
видах, действиях над ними;
- о матричным методом
методе решения системы трех линейных уравнений с тремя переменными;
воспитывать стремление к познанию, внимательное отношение к делу, аккуратность, самостоятельность, творческое отношение к учебной деятельности;
развивать логическое и аналитическое мышление; прививать интерес к поисковой деятельности.
Слайд 4
Математика является универсальным языком, который широко применяется во
всех сферах человеческой деятельности.
Во многих экономических и
профессиональных дисциплинах необходимы знания о матрицах, операциях над ними, умения решать прикладные задачи с помощью матриц.
Актуальность этой темы усиливается в связи
с широким использованием матриц в экономических дисциплинах: финансы, экономика предприятий, статистика, логистика, экономико – математическое моделирование и др.
Слайд 6
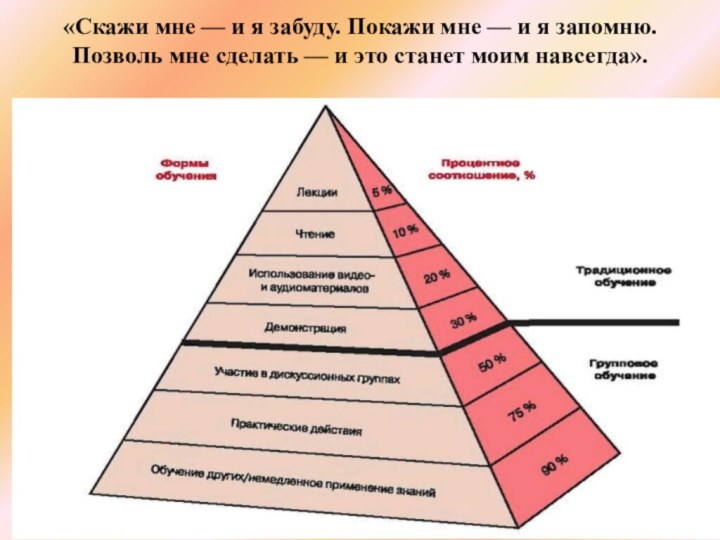
«Скажи мне — и я забуду. Покажи мне
— и я запомню. Позволь мне сделать — и
это станет моим навсегда».
Слайд 7
Основным применением матриц было решение линейных уравнений. После
развития теории определителей в конце 17-го века, Габриэль Крамер
начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли (Кэли, Кейли (Cayley) Артур английский математик). Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
Применение матриц
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами. К середине XIX в. матрицы стали самостоятельными объектами математических исследований. К этому времени были сформулированы правила сложения и умножения матриц. Основную роль в их разработке сыграли работы Гамильтона, Кэли и Сильвестра (J.J.Sylvester, 1814–1897). Современное обозначение матрицы предложил Кэли в 1841 году. Исследования Вейерштрасса (K.Th.W.Weierstrass, 1815–1897) и Фробениуса (F.G.L. Frobenius, 1849–1917) далеко продвинули теорию матриц, обогатив ее новым содержанием.
Слайд 13
Кэли, Кейли (Cayley) Артур английский математик
Джеймс Сильвестр –
один
из основоположников
теории матриц.
Фердинанд Георг Фробениус –
немецкий
математик.
Слайд 14
Мари Энмон Камиль (5 января 1838 - 22
января 1922) – французский математик...
Мари Энмон Камиль (5
января 1838 - 22 января 1922) – французский математик...
Слайд 15
Карл Теодор Вильгельм Вейерштрасс
Карл Теодор Вильгельм Вейерштрасс
Слайд 16
План
Применение матриц в экономике.
Слайд 17
Ключевые понятия и термины:
матрица;
определитель матрицы;
квадратная матрица;
прямоугольная матрица;
виды матриц;
обратная
матрица;
алгоритм нахождения обратной матрицы;
алгебраические дополнения.
Слайд 18
Литература
1. Алгебра и начала математического анализа: учебник
для общеобразоват. организаций: базов. и углубл. уровни / Ш.А.
Алимов, Ю.М. Колягин, М.В. Ткачева и др. – М.: Просвещение, 2016. – 463 с.
2. Высшая математика для экономистов: Учебное пособие. – К.: Знания, Макаренко В.А., 2008 – 517 с.
3. Математика: Учебник / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
4.Дидактический материал по математике: Учебное пособие / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001.
5. Практические занятия по математике. Н.В. Богомолов. – М.: Высшая школа, 1983.
Слайд 19
Вопросы к теме
Что такое матрицы и зачем
они нужны? Какие виды матриц существуют?
Как найти определитель матрицы?
Какие
операции можно выполнять над матрицами?
Какая матрица называется обратной?
Как найти обратную матрицу?
Как решить систему трех линейных уравнений с тремя переменными методом обратной матрицы?
Слайд 20
Актуализация опорных знаний студентов
Вопросы для фронтального опроса студентов
1.
Как вычисляется определитель второго порядка?
2. Вычислить определитель второго порядка:
Слайд 22
Актуализация опорных знаний студентов
Вопросы для фронтального опроса студентов
1.
Как вычисляется определитель второго порядка?
2. Вычислить определитель второго порядка:
3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
Слайд 23
Актуализация опорных знаний студентов
Вопросы для фронтального опроса студентов
1.
Как вычисляется определитель второго порядка?
2. Вычислить определитель второго порядка:
3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
Слайд 24
4. Проведем короткий анализ домашней работы.
5. Проверить
определитель второго порядка из домашнего задания
6. Проверить определитель третьего
порядка из домашнего задания
Слайд 25
1. Матрица – это упорядоченная таблица чисел которая
имеет m строк и n столбцов.
Слайд 26
Числа это элементы матрицы. Следует помнить, что
определитель – это величина, которую изображают в виде квадратной
таблицы; матрица – это всегда таблица чисел, никак по-другому не определяема.
Если , то матрица прямоугольная, если , то –
квадратная.
прямоугольная матрица размером
квадратная матрица ІІ порядка.
диагональная матрица ІІІ порядка.
Слайд 27
нулевая матрица размером
единичная матрица.
матрица - столбец.
матрица – строка.
Слайд 28
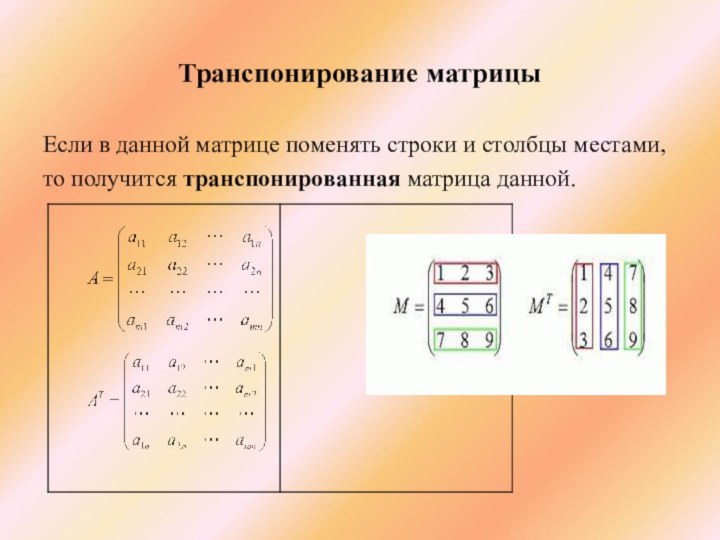
Транспонирование матрицы
Если в данной матрице поменять строки
и столбцы местами,
то получится транспонированная матрица данной.
Слайд 29
Где ещё применяются матрицы?
Теперь подробнее остановимся на некоторых
областях применения матриц.
Понятие матрицы и основанный на нем раздел
математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов.
Так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме.
С помощью матриц удобно записывать некоторые экономические зависимости.
Слайд 30
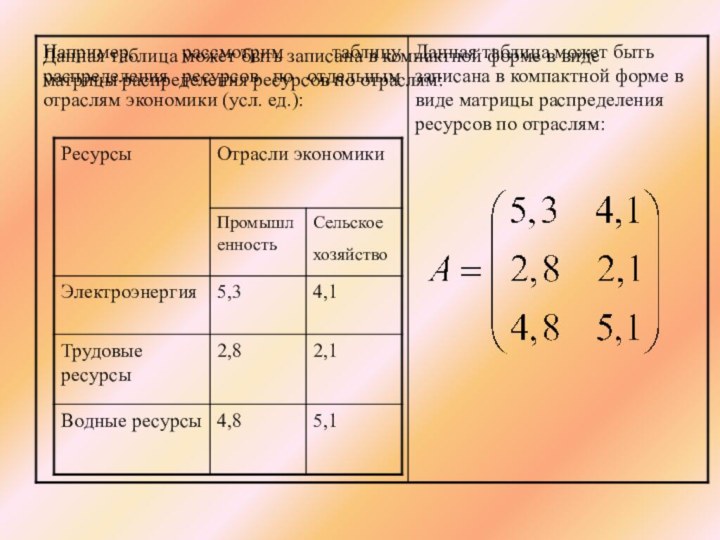
Данная таблица может быть записана в компактной форме
в виде матрицы распределения ресурсов по отраслям:
Слайд 31
В данной записи, например, матричный элемент показывает, сколько
электроэнергии употребляет промышленность, а элемент - сколько трудовых ресурсов
потребляет сельское хозяйство.
С помощью матриц можно решать системы уравнений, в них удобно представлять какие-либо данные.
Таким образом, мы пришли к выводу, что матрицы широко применялись и применяются до сих пор.
Слайд 32
2. Действия над матрицами.
Матрицы можно умножать
на число, складывать, умножать на матрицу.
Умножить матрицу
на число – это значит, каждый элемент умножить на это число.
Складывать можно матрицы одного размера. Суммой двух матриц является матрица, элементы которой равны сумме соответствующих элементов данных матриц. Так же определяется и разность.
Слайд 33
Свойства сложения и умножения матриц.
Слайд 34
Обратная матрица.
Матрицей
называют обратной к квадратной матрице А, если произведение
этих матриц равняется единичной матрицей, то есть
Обратная матрица существует для всякой невырожденной квадратной матрицы А, то есть когда определитель матрицы
Обратная матрица невырожденной квадратной матрицы А находится по формуле:
- определитель матрицы А, - алгебраические дополнения элементов определителя
.
Слайд 35
- определитель матрицы А,
- алгебраические дополнения элементов
определителя
Запишем алгоритм нахождения обратной матрицы для квадратной матрицы А:
1) вычислить определитель матрицы А. Если , то матрица А имеет обратную, в противном случае обратной матрицы не существует;
2) вычислить алгебраические дополнения элементов матрицы А;
3) Записать обратную матрицу
4) проверить правильность вычислений:
Алгебраические дополнения в обратной матрице записываются не по строкам, а по столбцам.
Слайд 36
Матрицы можно подвергать элементарным преобразованиям:
1. Можно менять местами
строки и столбцы.
2. Можно строку (столбец) умножать на
одно и то же число.
3. К некоторой строке или столбцу можно прибавить другую строку (столбец), умноженную на некоторое число.
Такие преобразования приводят к замене строк или столбцов строками (столбцами), состоящими из нулей, которые надо удалять из матрицы для рассмотрения матрицы меньшего размера.
Слайд 37
Пример1. Определить обратную матрицу
Нахождение обратной матрицы
Пример1. Определить
обратную матрицу
для матрицы
Решение. Вычислим определитель матрицы А:
то
для матрицы А существует обратная матрица .
Запишем алгебраические дополнения элементов матрицы А:
Слайд 38
Пример1. Определить обратную матрицу
Нахождение обратной матрицы
Пример1. Определить
обратную матрицу
для матрицы
Решение. Вычислим определитель матрицы А:
то
для матрицы А существует обратная матрица .
Запишем алгебраические дополнения элементов матрицы А:
Слайд 39
Проверка правильности вычислений:
(Сделать вывод. Для матриц А и справедлив переместительный закон умножения).
Делаем вывод. Для матриц А и справедлив переместительный закон умножения.
Ответ:
Слайд 40
Пример Определить обратную матрицу
для матрицы
Слайд 41
Пример Определить обратную матрицу
для матрицы
Слайд 42
Пример Определить обратную матрицу
для матрицы
Слайд 43
Пример Определить обратную матрицу
для матрицы
Слайд 44
Пример Определить обратную матрицу
для матрицы
Слайд 45
Пример Определить обратную матрицу
для матрицы
Слайд 46
Пример Определить обратную матрицу
для матрицы
Слайд 48
Пример Определить обратную матрицу
для матрицы
Решение. Вычислим определитель матрицы А:
то для матрицы
А существует обратная матрица
Запишем алгебраические дополнения элементов матрицы А:
Обратная матрица имеет вид:
Слайд 52
Решение система трех линейных уравнений с тремя неизвестными
методом обратной матрицы
Пусть задана система трех линейных уравнений с
тремя неизвестными
Если основная матрица системы линейных уравнений
является квадратной и невырожденной, то систему можно решить матричным способом (с помощью обратной матрицы). Записав систему в матричном виде, получим решение X системы уравнений:
А- матрица, составленная из коэффициентов при переменных x. y. z .
Х- матрица – столбец составленная из переменных величин.
В- матрица – столбец составленная из свободных членов.
Слайд 53
Пример 1. Решить систему трех линейных уравнений с
тремя неизвестными методом обратной матрицы:
Решение. Запишем систему в матричном
виде , где
Решение матричного уравнения будет иметь вид:
Найдем обратную матрицу
Сначала найдем главный определитель матрицы:
Слайд 54
Теперь будем находить алгебраические дополнения:
Слайд 55
Теперь будем находить алгебраические дополнения:
Слайд 56
Теперь будем находить алгебраические дополнения:
, то умножим обратную матрицу
на матрицу столбец :
, то умножим обратную матрицу
на матрицу столбец :
, то умножим обратную матрицу
на матрицу столбец :
Ответ:
, то умножим обратную матрицу
на матрицу столбец :
Проверка:
Ответ:
Слайд 61
Задача 1. В цехе предприятия изготовляют две модели
женской одежды. На изготовление первой модели тратят 2 м
ткани, на изготовление второй – 3 м. При этом расходы рабочего времени на производство этих моделей составляют соответственно 4 и 5 часов. Известно, что недельный запас ткани – 100 м, а рабочее время ограниченно 190 часов.
Составить такой план недельного изготовления этих моделей одежды, при которой полностью используют ресурсы (ткань и рабочее время).
Слайд 62
Применение матриц в экономике
Задача 1. В цехе предприятия
изготовляют две модели женской одежды. На изготовление первой модели
тратят 2 м ткани, на изготовление второй – 3 м. При этом расходы рабочего времени на производство этих моделей составляют соответственно 4 и 5 часов. Известно, что недельный запас ткани – 100 м, а рабочее время ограниченно 190 часов.
Составить такой план недельного изготовления этих моделей одежды, при которой полностью используют ресурсы (ткань и рабочее время).
Обозначим через и количество единиц недельного выпуска первой и второй моделей соответственно. По условию задачи составим систему линейных уравнений
Слайд 63
Применение матриц в экономике
Задача 1. В цехе предприятия
изготовляют две модели женской одежды. На изготовление первой модели
тратят 2 м ткани, на изготовление второй – 3 м. При этом расходы рабочего времени на производство этих моделей составляют соответственно 4 и 5 часов. Известно, что недельный запас ткани – 100 м, а рабочее время ограниченно 190 часов.
Составить такой план недельного изготовления этих моделей одежды, при которой полностью используют ресурсы (ткань и рабочее время).
Обозначим через и количество единиц недельного выпуска первой и второй моделей соответственно. По условию задачи составим систему линейных уравнений
Слайд 64
Решение. Какие методы известны из школьного курса? (Метод
подстановки, метод сложения, графический метод).
Какой метод изучили в колледже?
Решим
эту систему матричным способом. Запишем ее в матричном виде:
Для матрицы А найдем обратную матрицу . Поскольку
, тогда
Получим решение системы
Слайд 65
Решение. Какие методы известны из школьного курса? (Метод
подстановки, метод сложения, графический метод).
Какой метод изучили в колледже?
Решим
эту систему матричным способом. Запишем ее в матричном виде:
Для матрицы А найдем обратную матрицу . Поскольку
, тогда
Получим решение системы
Слайд 66
Следовательно, для полного использования ресурсов еженедельно нужно изготовлять
35 единиц первой и 10 единиц второй моделей одежды.
Вывод.
Заметим, что при решении экономических задач удобно использовать матричный способ. Почему?
Вычислив один раз обратную матрицу и изменяя ограничение на ресурсы (ежедневные, еженедельные, ежемесячные, ежегодные и тому подобное), будем получать каждый раз из равенства соответствующий план выпуска продукции.
Заметим, что применение матриц в этой задаче привело к наглядности, упрощению и компактности вычислений.
Слайд 67
Задача № 2. Рассмотрим упрощенную модель финансовой
математики, которую условно называют «портфельными инвестициями».
В реальной жизни
одним из источников финансирования являются международные инвестиции. Страна может получать и давать международные займы, принимать и инвестировать за границу капитал. Продажа активов в любой фирме (права собственности, ценные бумаги, золото и т.п.) означает прилив капитала в страну. Среди инвестиций есть портфельные – вложение капитала в иностранные ценные бумаги, которые не дают инвестору права реального контроля над объектом инвестирования. Такие инвестиции основываются, как правило, на частном капитале.
Слайд 68
$ 40 000
Допустим, что инвесторы могут вкладывать деньги в
активы, в облигации (которые дают точную финансовую прибыль), акции
(дают прибыль, которая может меняться), в землю. Пусть после выборов в данной стране к власти может прийти одна из двух политических партий или . Понятно, что доход от капиталовложения зависит от государственного правительства страны.
Итак, правительство партии может увеличивать цену на землю и уменьшать цену акций, а правительство партии - наоборот. Например, имеем таблицу:
Слайд 69
Данную таблицу можно записать как матрицу
размера 3×2,
что означает доход от каждого актива:
Пусть инвесторы решили
вложить $ 50 000 в землю, $ 100 000 – в облигации и $ 40 000 – в акции. Тогда получим матрицу – строку Р размера 1×3: , которая характеризует портфельные инвестиции.
Произведение матриц PR будет матрица размера 1×2, которая характеризует возможные стоимости портфельных инвестиций, если на выборах победит партия или
Можно сделать вывод, если на выборах победит партия , то стоимость портфеля составит $ 203 500, а если партия -то $ 198 500. Ваш выбор? Какой партии дадите предпочтение?
.
Слайд 70
Самостоятельная работа
( 7 мин. ) (Решить один из
уровней)
Заданы матрицы
І уровень:
Найти А+В; А-В; С=3А- 2В,
.
ІІ уровень:
2. Найти произведение матриц АВ.
ІІІ уровень:
3. Найти матрицу обратную матрице А и сделать проверку.
Слайд 71
Домашнее задание (n-ваш номер в списке группы)
1. Выучить
теоретический материал по теме, с использованием опорного конспекта и
учебной литературы. 2. Выполнить задания:
І уровень:
1. Заданы матрицы .
а) Найти А+В; А-В;С =3А- 2В, , АВ.
б) Найти матрицу обратную матрице А и сделать проверку.
ІІ уровень: Решить, заданную на предыдущем занятии, систему линейных алгебраических уравнений с помощью обратной матрицы. (Системы прилагаются) (Каждый студент берет систему, соответствующему номеру в классном журнале)
Слайд 72
Подведение итогов занятия.
Какие основные определения и понятия вы
усвоили на занятии?
С каким способом решения системы вы сегодня
познакомились?
Слайд 73
Подведение итогов занятия.
Какие основные определения и понятия вы
усвоили на занятии?
познакомились с матрицами, с видами матриц, с
действиями над матрицами, с обратной матрицей, с алгоритмом нахождения обратной матрицы.
С каким способом решения системы вы сегодня познакомились?
Метод обратной матрицы.
Слайд 74
Подведение итогов занятия.
Благодарю за работу на занятии.
Подсчитываем
поощрительные баллы.
Оценки комментируются и выставляются в журнал.
Слайд 75
Проверьте сами.
Сделайте вывод! Квадрат Пифагора!
Дата
Рождения! (25.07.1998)