Слайд 2
Цель урока –
ознакомить с геометрическим телом – призмой
(с её основными элементами, видами, формула для вычисления площади
и объема), симметрией, с понятием многогранники.
Платоновы тела
Слайд 3
Нас окружают предметы разной геометрической формы.
(здание имеет форму четырехугольной призмы)
Слайд 4
Пчелиные соты имеют форму шестиугольной призмы.
Слайд 5
И пирамиды в Египте и горные кристаллы, и
башни кремля
– все они имеют форму пирамиды
Слайд 6
Форму цилиндра имеют хранилище для зерна – элеватор,
ангары и даже кухонная утварь.
Слайд 7
Форму конуса имеют многие предметы, которые нас окружают:
терриконы и зернохранилища, и стаканчики для мороженного.
Слайд 8
Предметы сферической формы самые распространенные: от футбольного мяча
до нашей планеты – Земля.
Слайд 9
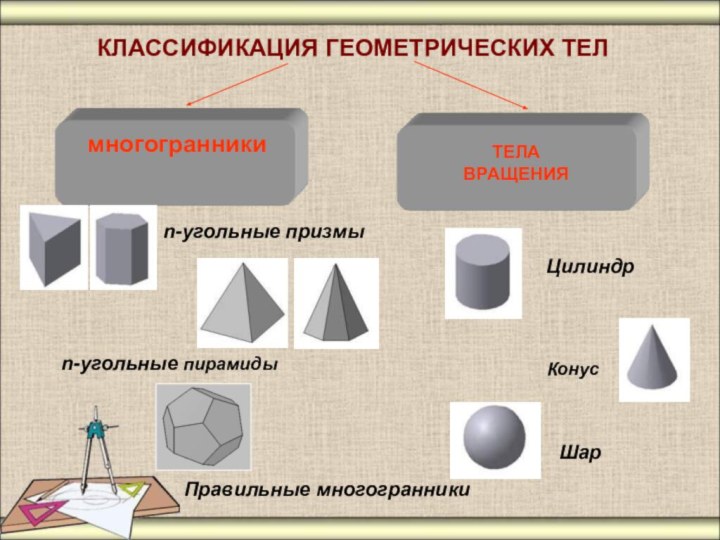
КЛАССИФИКАЦИЯ ГЕОМЕТРИЧЕСКИХ ТЕЛ
ТЕЛА ВРАЩЕНИЯ
многогранники
n-угольные пирамиды
Конус
n-угольные призмы
Цилиндр
Шар
Правильные многогранники
Слайд 10
Многогранник- это тело, поверхность которого состоит из конечного
числа плоских многоугольников.
Слайд 11
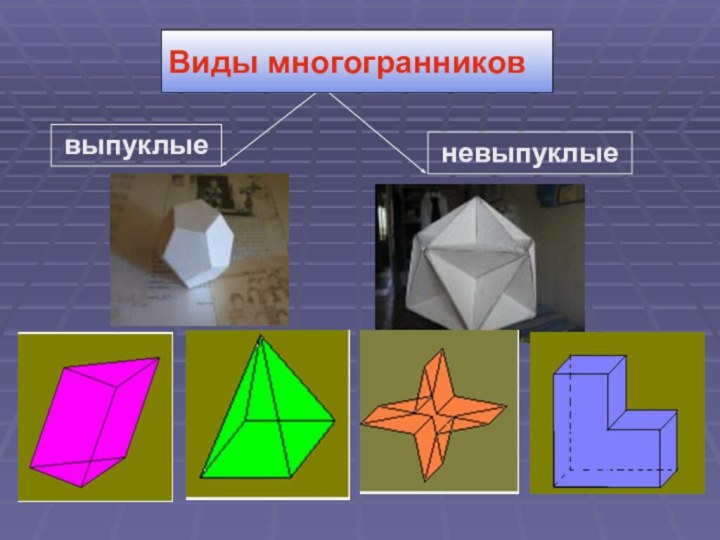
выпуклые
невыпуклые
Виды многогранников
Слайд 12
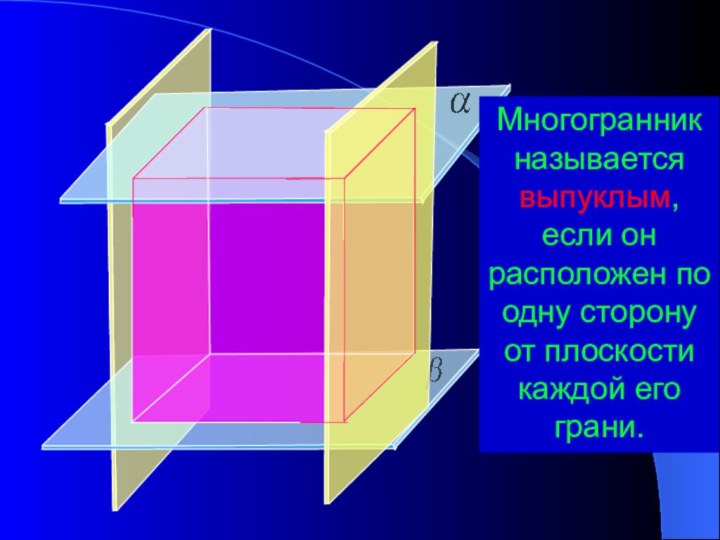
Выпуклый многогранник
Многогранник называется выпуклым, если он расположен по
одну сторону от плоскости каждой его грани.
Все грани выпуклого
многогранника являются выпуклыми многоугольниками.
В выпуклом многограннике
сумма всех плоских углов
при каждой его вершине
меньше 360 градусов.
Слайд 13
Многогранник называется выпуклым, если он расположен по одну
сторону от плоскости каждой его грани.
Слайд 14
Невыпуклый многогранник – многогранник, расположенный по разные стороны
от плоскости одной из его граней.
Слайд 15
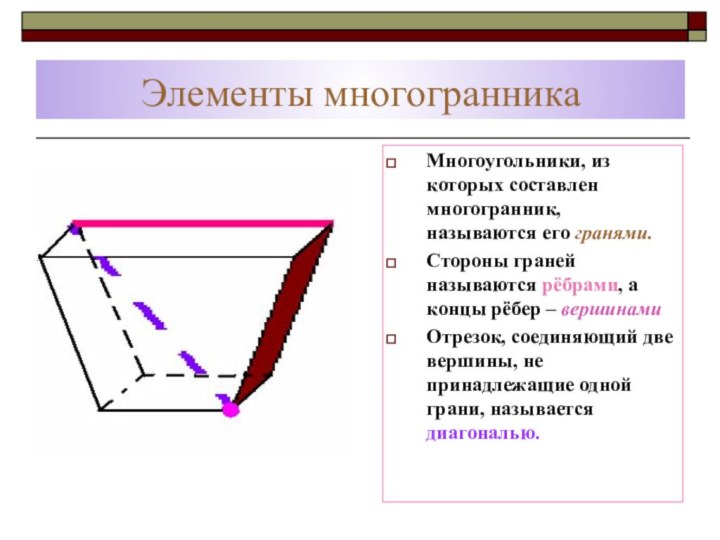
Элементы многогранника
Многоугольники, из которых составлен многогранник, называются его
гранями.
Стороны граней называются рёбрами, а концы рёбер – вершинами
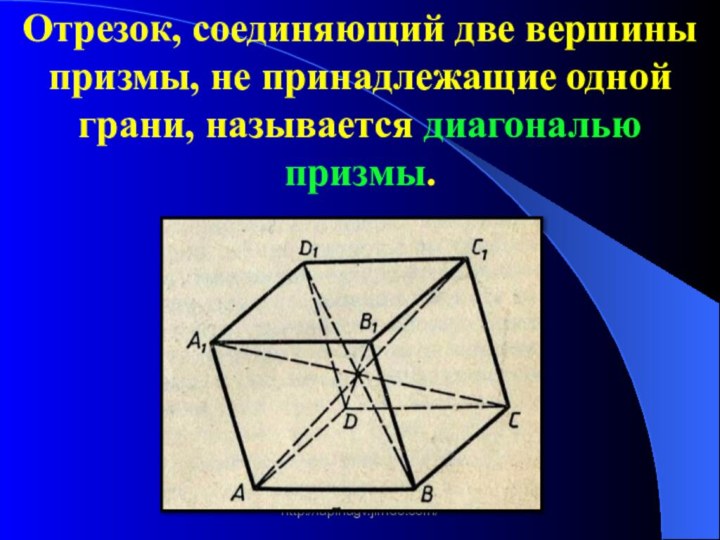
Отрезок,
соединяющий две вершины, не принадлежащие одной грани, называется диагональю.
Слайд 16
Правильные многогранники
Если грани многогранника являются правильными многоугольниками с
одним и тем же числом сторон и в каждой
вершине многогранника сходится одно и то же число ребер, то выпуклый многогранник называется правильным.
Слайд 17
Многогранник правильный, если все его грани – правильные
равные многоугольники и все двугранные углы равны.
Свойства правильных многогранников:
все
ребра равны;
все плоские углы равны;
все многогранные углы равны;
все многогранные углы имеют одно и то же число граней, и в каждой вершине сходится одно и то же число ребер.
Слайд 18
Правильные многогранники
Пифагорейцы считали правильные многогранники божественными фигурами. Праосновам
бытия приписывалась форма правильных многогранников.
Учение пифагорейцев изложил в
своих трудах Платон. С тех пор правильные многогранники называют платоновыми телами.
Евклид доказал, что других правильных многогранников не существует.
Слайд 19
Платоновы тела.
Представители семейства.
Слайд 20
Тетраэдр - это треугольная пирамида, гранями которой являются
треугольники
Слайд 21
Октаэдр - это многогранник, гранями которого являются правильные
треугольники и в каждой вершине сходится 4 грани.
Правильная форма
алмаза – октаэдр
Слайд 22
Гексаэдр (куб) - это многогранник, в каждой вершине
которого сходится 3 квадрата.
Кристаллы поваренной соли имеют форму куба
Слайд 23
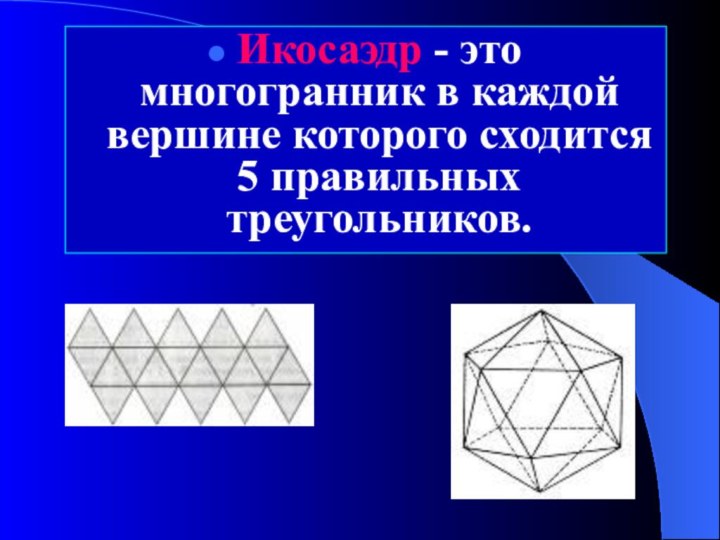
Икосаэдр - это многогранник в каждой вершине которого
сходится 5 правильных треугольников.
Слайд 24
Додекаэдр - это многогранник, в каждой вершине которого
сходится 3 правильных многоугольника.
Кристаллы пирита – додекаэдра
Слайд 26
Призма
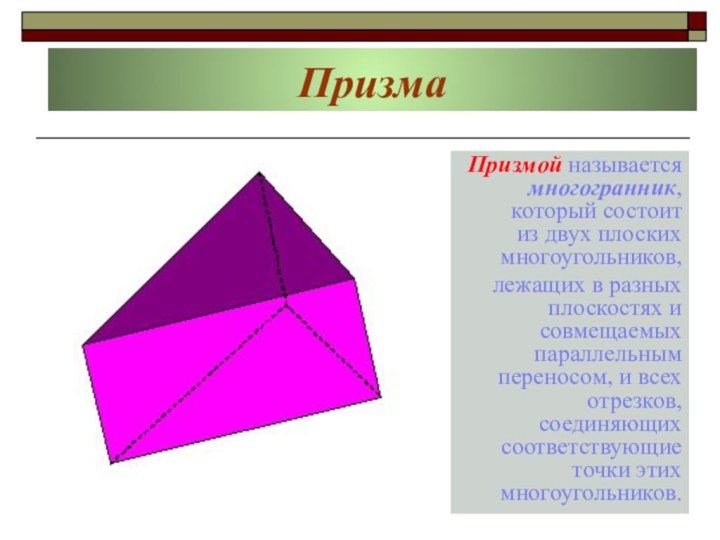
Призмой называется многогранник, который состоит из двух плоских
многоугольников,
лежащих в разных плоскостях и совмещаемых параллельным
переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.
Слайд 27
Призма
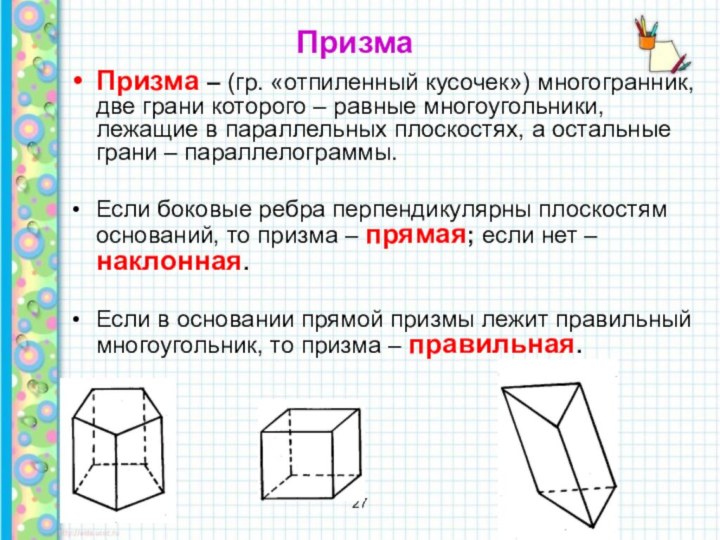
Призма – (гр. «отпиленный кусочек») многогранник, две
грани которого – равные многоугольники, лежащие в параллельных плоскостях,
а остальные грани – параллелограммы.
Если боковые ребра перпендикулярны плоскостям оснований, то призма – прямая; если нет – наклонная.
Если в основании прямой призмы лежит правильный многоугольник, то призма – правильная.
Слайд 28
Построение изображения призмы:
1. строят основание
(нижнее или верхнее
– многоугольник);
2. из вершин многоугольника строят параллельные прямые;
3. на
прямых откладывают равные отрезки (высота призмы);
4. соединяют полученные точки (концы отрезков), получая второе основание.
Слайд 29
Виды призм
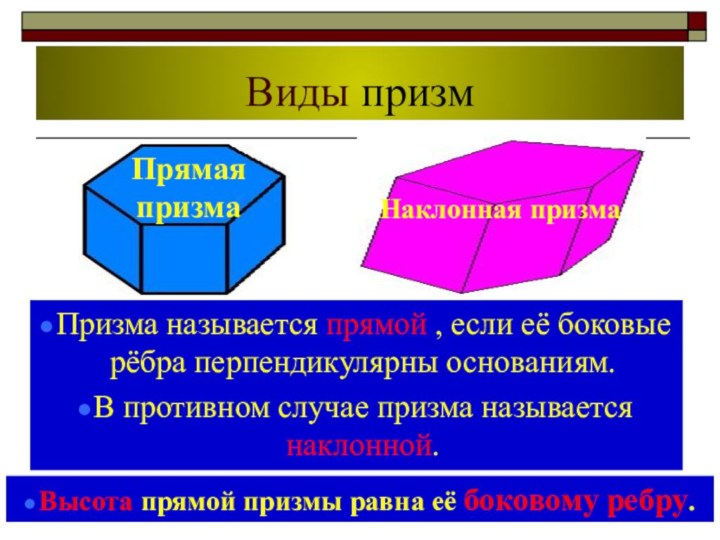
Прямая призма
Наклонная призма
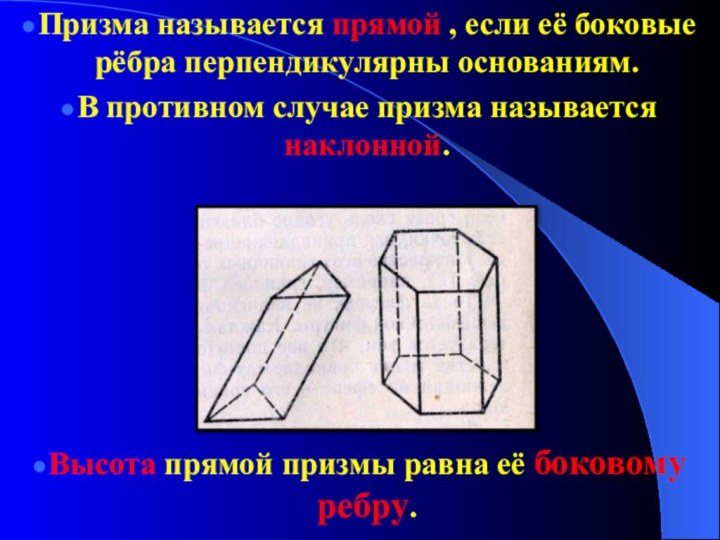
Призма называется прямой , если
её боковые рёбра перпендикулярны основаниям.
В противном случае призма называется
наклонной.
Высота прямой призмы равна её боковому ребру.
Слайд 30
Призма называется прямой , если её боковые рёбра
перпендикулярны основаниям.
В противном случае призма называется наклонной.
Высота прямой призмы
равна её боковому ребру.
Слайд 31
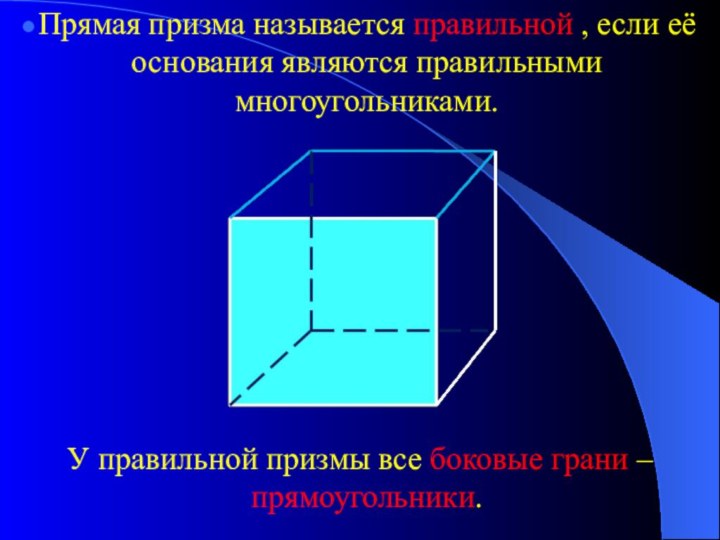
Прямая призма называется правильной , если её основания
являются правильными многоугольниками.
У правильной призмы все боковые грани –
прямоугольники.
Слайд 32
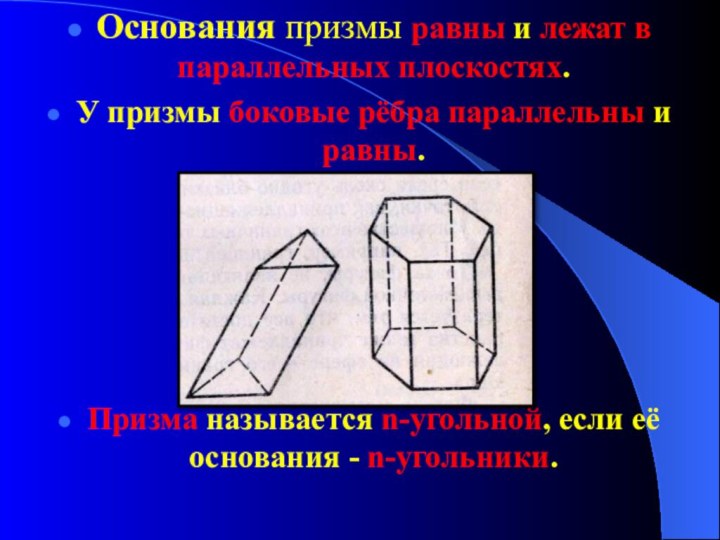
Основания призмы равны и лежат в параллельных плоскостях.
У
призмы боковые рёбра параллельны и равны.
Призма называется n-угольной, если
её основания - n-угольники.
Слайд 33
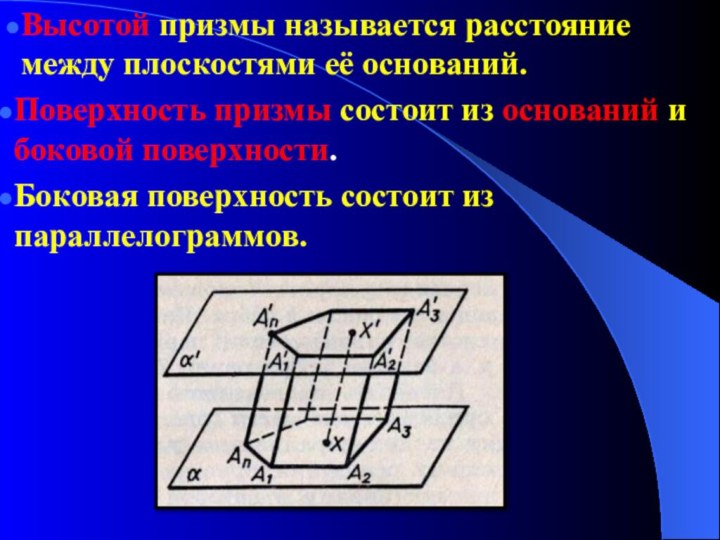
Высотой призмы называется расстояние между плоскостями её оснований.
Поверхность
призмы состоит из оснований и боковой поверхности.
Боковая поверхность
состоит из параллелограммов.
Слайд 34
Отрезок, соединяющий две вершины призмы, не принадлежащие одной
грани, называется диагональю призмы.
http://lapinagv.jimdo.com/
Слайд 35
Площадью полной поверхности призмы называется сумма площадей всех
её граней.
Sпол=Sбок+2Sосн
Слайд 36
Объём прямоугольного параллелепипеда вычисляется по формуле:
V=abc
Объём любого прямоугольного
параллелепипеда равен произведению площади егооснования на высоту:
V=SоснH
Слайд 37
Основные свойства параллелепипеда
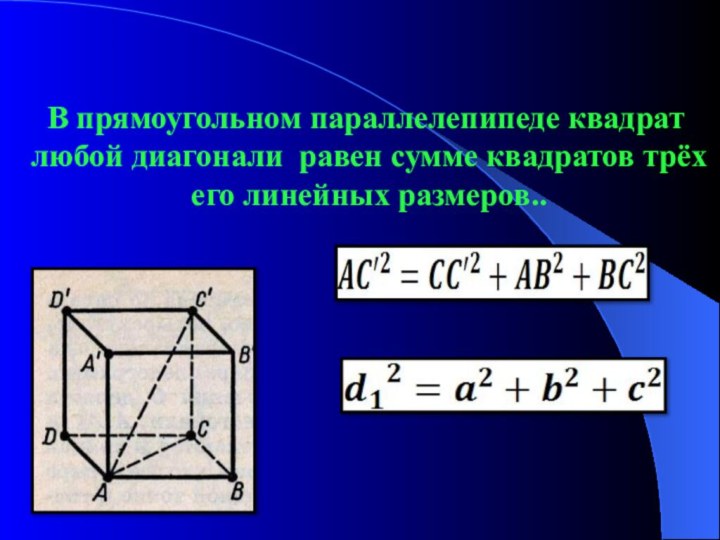
В прямоугольном параллелепипеде квадрат любой диагонали
равен сумме квадратов трёх его линейных размеров..
Слайд 38
Самостоятельная работа
Изобразите треугольную и четырёхугольную призмы.
Обозначьте их,
проведите диагонали и высоты, выпишите все элементы:
- вершины;
-
основания;
- боковые рёбра;
- боковые грани;
- высоты;
- диагонали.
Слайд 39
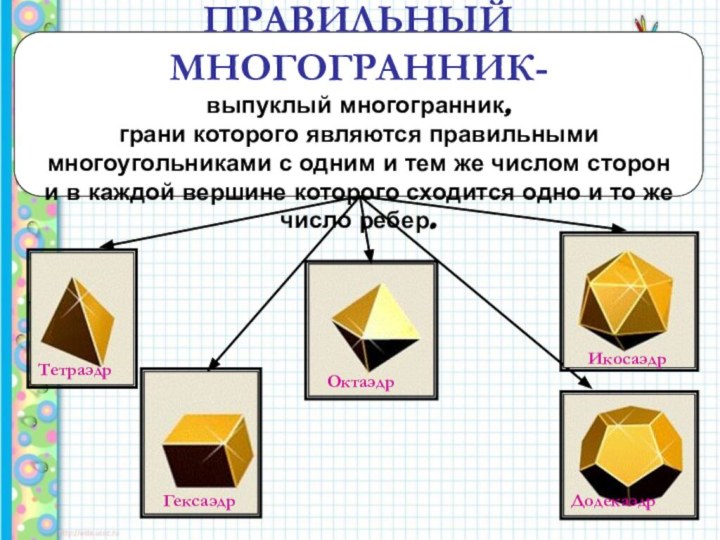
ПРАВИЛЬНЫЙ МНОГОГРАННИК-
выпуклый многогранник,
грани которого являются правильными
многоугольниками
с одним и тем же числом сторон
и в
каждой вершине которого сходится одно и то же число ребер.
Гексаэдр
Тетраэдр
Октаэдр
Додекаэдр
Икосаэдр
Слайд 41
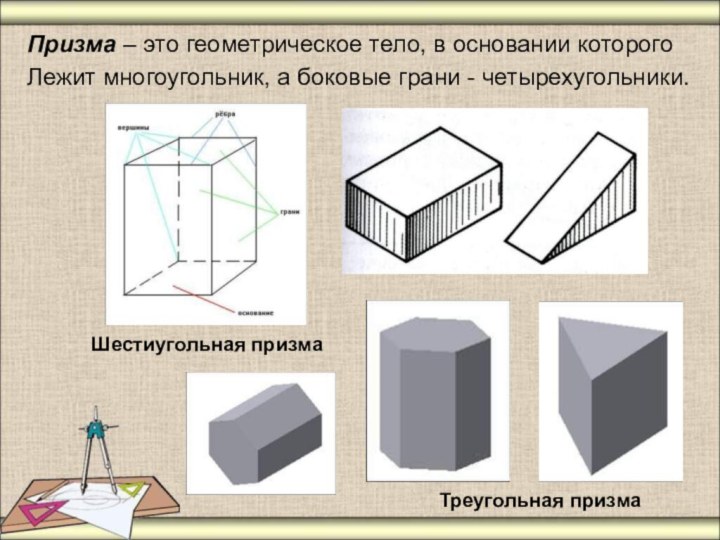
Призма – это геометрическое тело, в основании которого
Лежит многоугольник, а боковые грани - четырехугольники.
Шестиугольная призма
Треугольная призма
Слайд 42
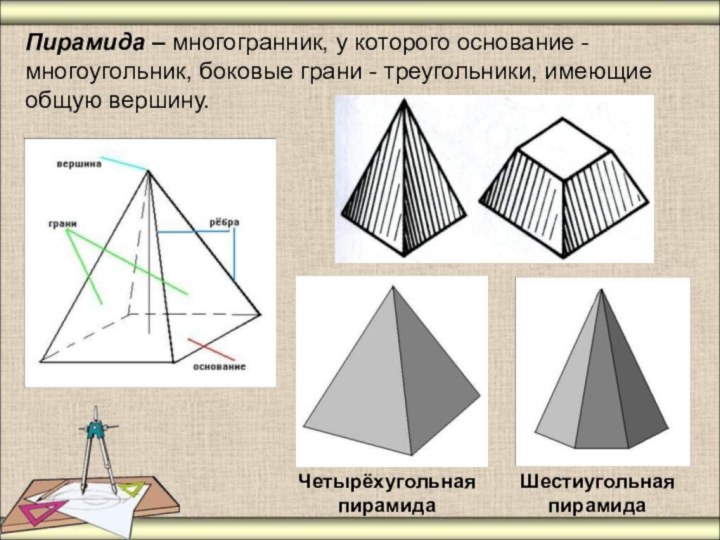
Пирамида – многогранник, у которого основание - многоугольник,
боковые грани - треугольники, имеющие общую вершину.
Четырёхугольная пирамида
Шестиугольная пирамида
Слайд 43
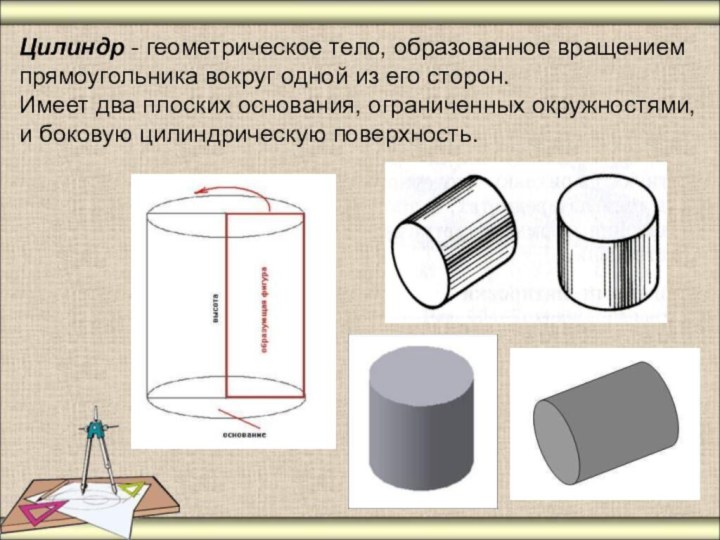
Цилиндр - геометрическое тело, образованное вращением прямоугольника вокруг
одной из его сторон.
Имеет два плоских основания, ограниченных окружностями,
и боковую цилиндрическую поверхность.
Слайд 44
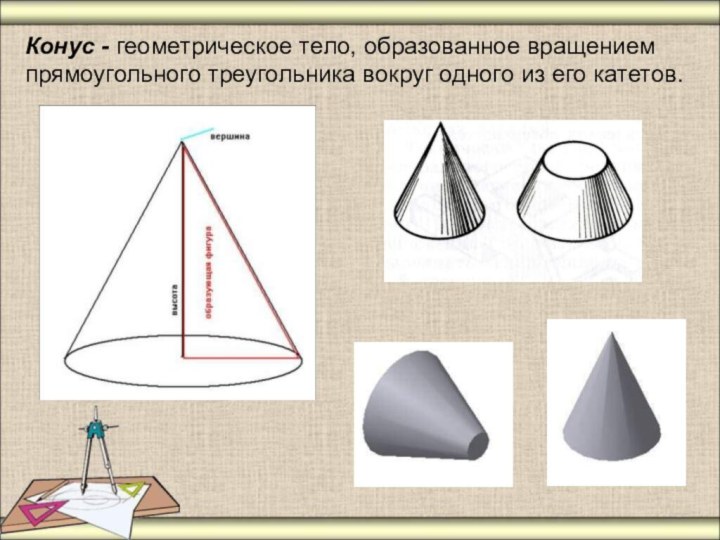
Конус - геометрическое тело, образованное вращением прямоугольного треугольника
вокруг одного из его катетов.
Слайд 45
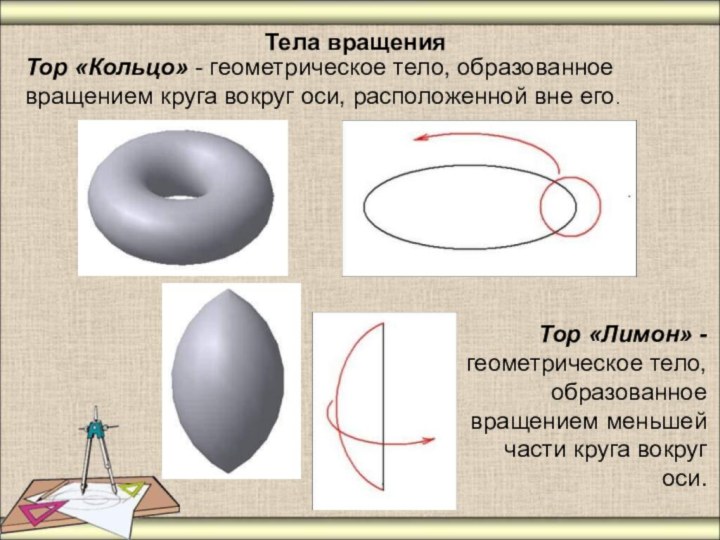
Тор «Кольцо» - геометрическое тело, образованное вращением круга
вокруг оси, расположенной вне его.
Тор «Лимон» - геометрическое тело,
образованное вращением меньшей части круга вокруг оси.
Тела вращения
Слайд 46
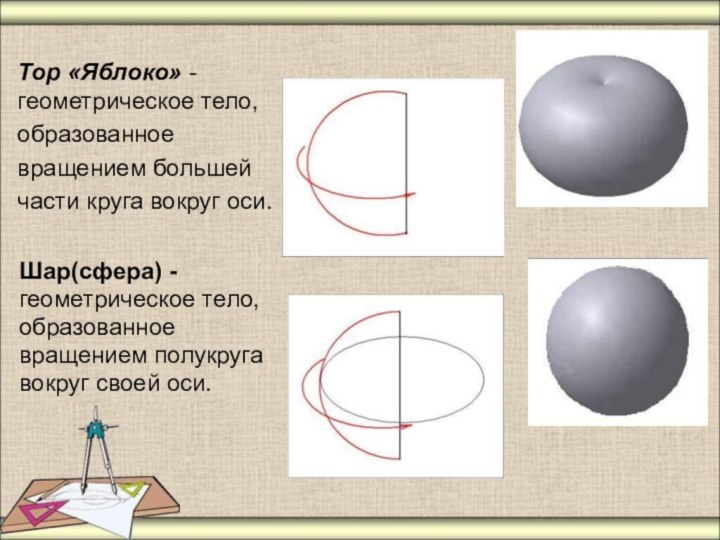
Тор «Яблоко» -
геометрическое тело,
образованное
вращением большей
части
круга вокруг оси.
Шар(сфера) -
геометрическое тело,
образованное
вращением полукруга
вокруг своей
оси.
Слайд 47
Задача
Три латунных куба с рёбрами 3 см,
4 см и 5 см переплавлены в один куб.
Какую длину имеет ребро этого куба?
http://lapinagv.jimdo.com/
Слайд 48
Задача
Требуется установить резервуар для воды ёмкостью 15 м3
на прямоугольной площадке размером 2,5*1,5 м,
служащий для него
дном.
Найдите высоту резервуара?
Слайд 49
Аквариум имеет форму прямоугольного параллелепипеда высотой 30
см. Если в него налить 30 л. воды, то
до верхнего края останется 5 см. Сколько литров воды нужно, чтобы наполнить пустой аквариум доверху?
Задача
Слайд 50
Решение.
Пусть V и H соответственно объем и
высота параллелепипеда.
V=SH . По условию V=30,H=25, тогда 25*S=30.
После
заполнения пустого аквариума доверху H=30. Значит, 30*S=V.
Найдем отношение = , V=36 л.
Ответ: 36.