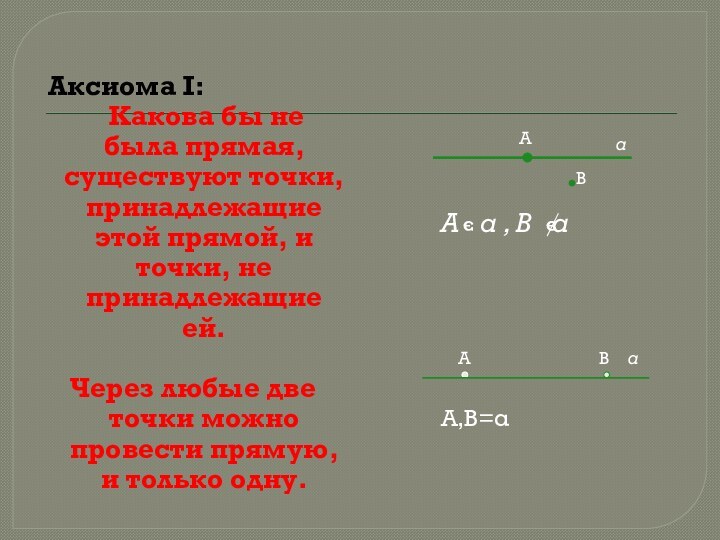
прямая, существуют точки, принадлежащие этой прямой, и точки, не
принадлежащие ей.Через любые две точки можно провести прямую, и только одну.
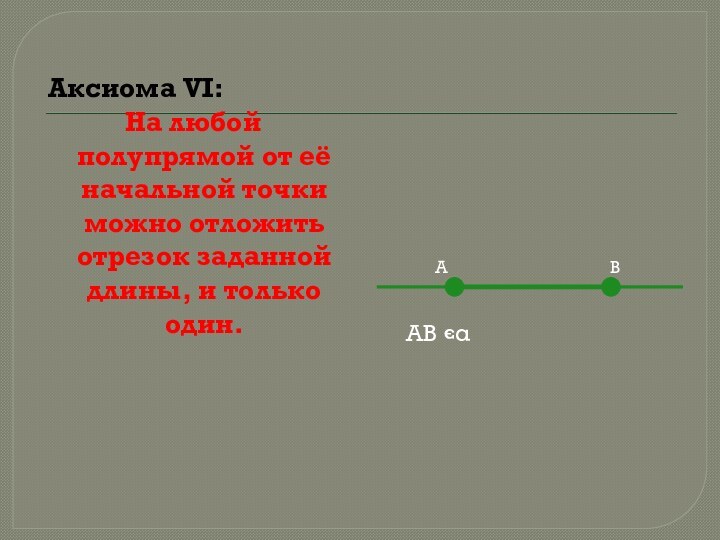
А α , В α
Э
Э
А
В
А,В=α
α
α
А
В
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









А α , В α
Э
Э
А
В
А,В=α
α
α
А
В
А
В
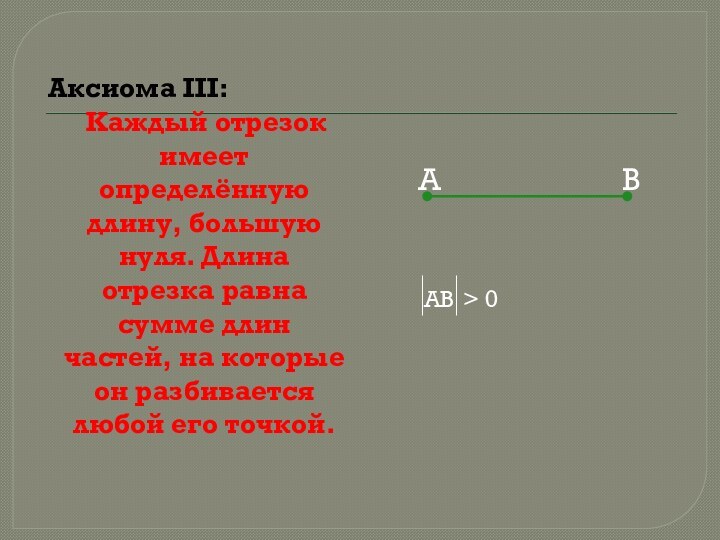
АВ > 0
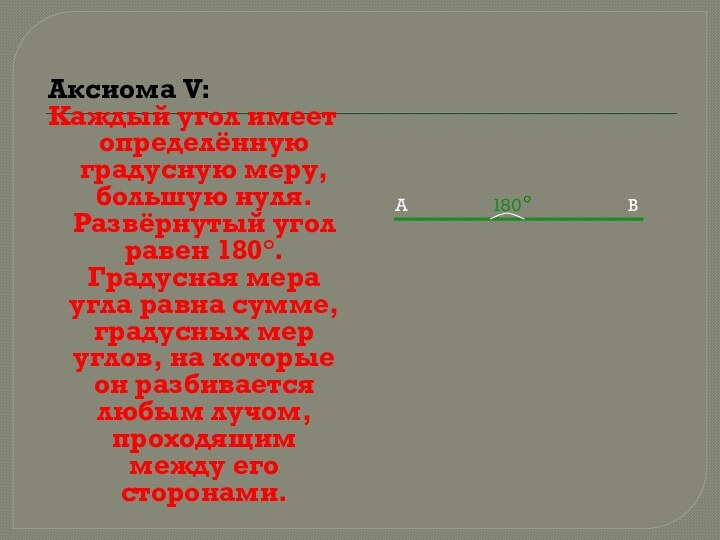
180
В
А
Э
α
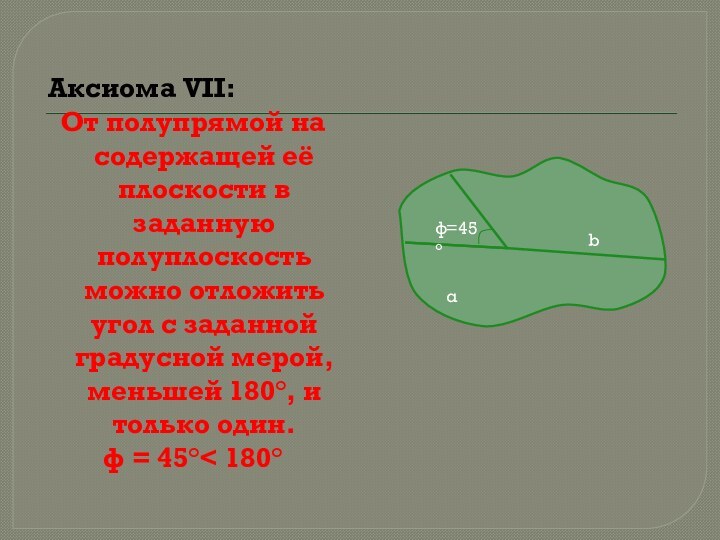
b
φ=45°
α
а
А
В
С
А1
В1
С1
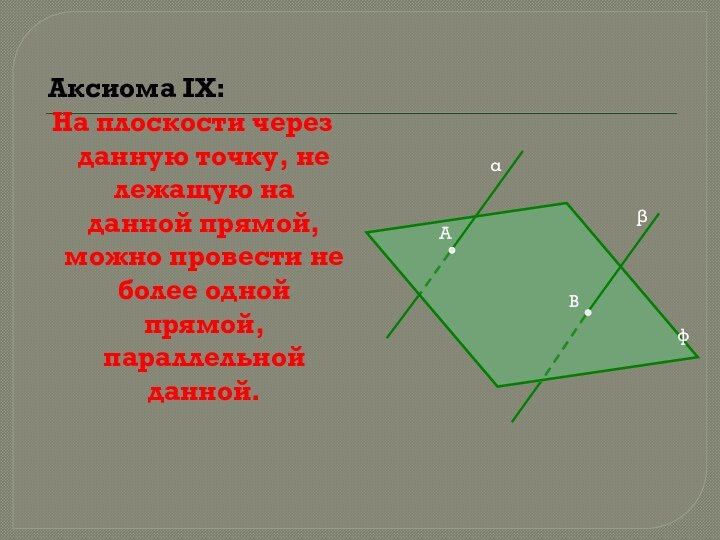
А
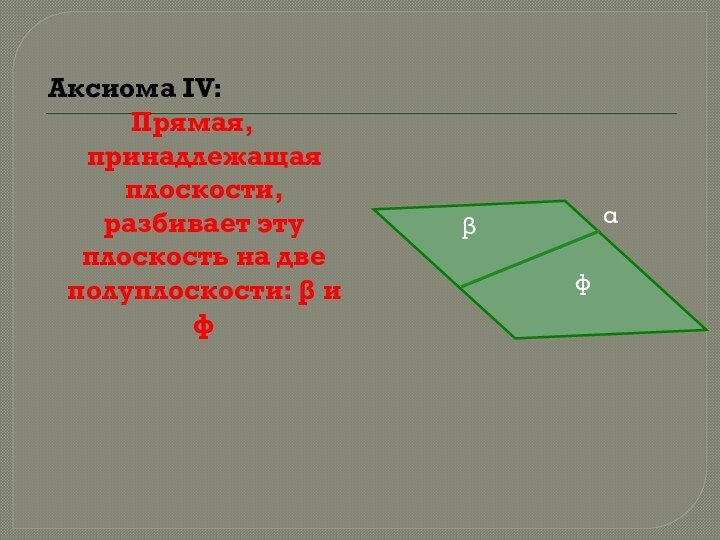
α
β
φ
B