- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Показательная функция, её график и свойства.
Содержание
- 2. Цель:Рассмотрение основных свойств показательной функции.Построение графика.Решение показательных уравнений.Решение показательных неравенств.
- 3. ОпределениеПоказательная функция – это функция вида
- 4. Свойства показательной функции Область определения: все
- 5. График показательной функцииТ.к.
- 6. Показательные уравненияОпределениеПростейшие уравненияСпособы решения сложных уравнений
- 7. Определение Уравнение, в котором переменная содержится в показателе степени, называется показательным. Примеры:
- 8. Простейшее показательное уравнение – это уравнение вида Простейшее показательное уравнение решается с использованием свойств степени.
- 9. Способы решения сложных показательных уравнений.Вынесение за скобки степени с меньшим показателемЗамена переменнойДеление на показательную функцию
- 10. Вынесение за скобки степени с меньшим показателемДанный
- 11. Замена переменнойПри данном способе показательное уравнение сводится
- 12. Деление на показательную функциюДанный способ используется, если
- 13. Показательные неравенстваОпределениеПростейшие неравенстваРешение неравенств
- 14. Определение Показательные неравенства – это неравенства, в которых неизвестное содержится в показателе степени.Примеры:
- 15. Простейшие показательные неравенства – это неравенства вида:где
- 16. При решении простейших неравенств используют
- 17. Показательная функция Построение графикаСравнение чисел с использованием
- 18. Задача 1 Построить график функции y
- 19. Задача 2 Сравнить числа РешениеОтвет:
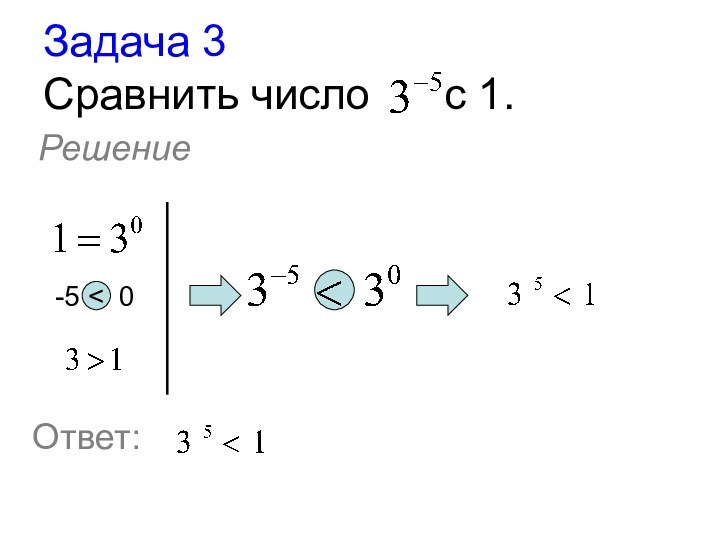
- 20. Задача 3 Сравнить число с 1. Решение-5 < 0Ответ:
- 21. Задача 4 Cравнить число р
- 22. Решение показательных уравнений Простейшие показательные уравненияУравнения, решаемые
- 23. Простейшие показательные уравненияОтвет: - 5,5.Ответ: 0; 3.
- 24. Вынесение за скобки степени с меньшим показателемОтвет:
- 25. Замена переменной (1)основания степеней одинаковы, показатель одной
- 26. Замена переменной (2)Основания степеней одинаковы, коэффициенты перед переменной противоположны. По т. Виета:- Не удовлетворяет условиюОтвет: 1
- 27. Деление на показательную функциюОтвет: 0
- 28. Деление на показательную функциюОтвет: 0; 1.
- 29. Простейшие показательные неравенстваДвойные неравенстваНеравенства, решаемые вынесением за
- 30. Простейшие показательные неравенства
- 31. Двойные неравенстваОтвет: (- 4; -1).3 > 1, то
- 32. Решение показательных неравенствМетод: Вынесение за скобки
- 33. Скачать презентацию
- 34. Похожие презентации
Цель:Рассмотрение основных свойств показательной функции.Построение графика.Решение показательных уравнений.Решение показательных неравенств.

























Слайд 2
Цель:
Рассмотрение основных свойств показательной функции.
Построение графика.
Решение показательных уравнений.
Решение
показательных неравенств.
Слайд 3
Определение
Показательная функция – это функция вида
,
где
x – переменная,- заданное число, >0, ≠1.
Примеры:
Слайд 4
Свойства показательной функции
Область определения:
все действительные числа
Множество значений:
все положительные числа
При >
1 функция возрастающая;
при 0 < < 1 функция убывающая.D(y) = R;
E(y) = (0; + ∞);
Слайд 5
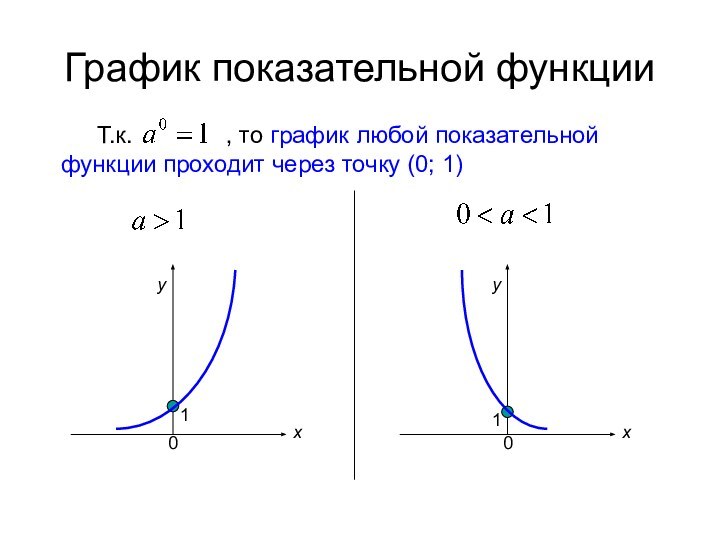
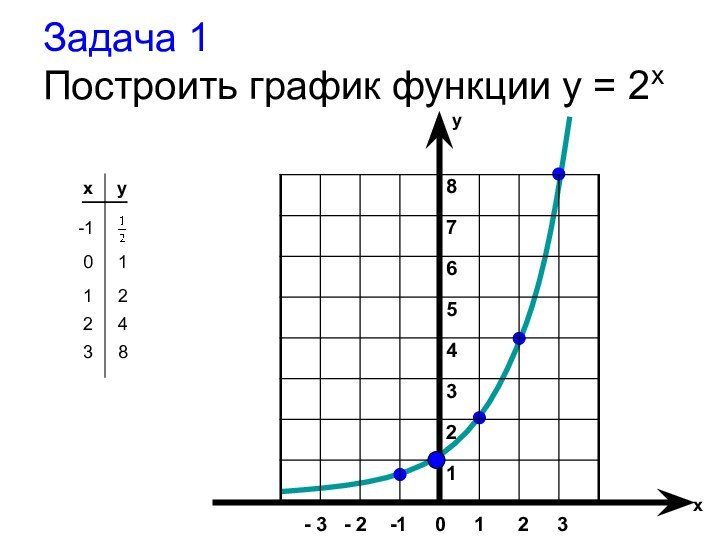
График показательной функции
Т.к.
, то график любой показательной функции проходит через
точку (0; 1)1
1
х
х
у
у
0
0
Слайд 7
Определение
Уравнение, в котором переменная содержится в
показателе степени, называется показательным.
Примеры:
Слайд 8
Простейшее показательное уравнение – это уравнение вида
Простейшее
показательное уравнение решается с использованием свойств степени.
Слайд 9
Способы решения сложных показательных уравнений.
Вынесение за скобки степени
с меньшим показателем
Замена переменной
Деление на показательную функцию
Слайд 10
Вынесение за скобки степени с меньшим показателем
Данный способ
используется, если соблюдаются два условия:
1) основания степеней
одинаковы;2) коэффициенты перед
переменной одинаковы
Например:
Слайд 11
Замена переменной
При данном способе показательное уравнение сводится к
квадратному.
Способ замены переменной используют, если
показатель одной из степеней в
2 раза больше, чем у другой.
Например:
3 2x – 4 · 3 х – 45 = 0
коэффициенты перед
переменной противоположны.
Например:
2 2 - х – 2 х – 1 =1
б)
а) основания степеней одинаковы;
Слайд 12
Деление на показательную функцию
Данный способ используется, если основания
степеней разные.
а) в уравнении вида ax = bx делим
на bxНапример: 2х = 5х | : 5x
б) в уравнении A a2x + B (ab)x + C b2x = 0
делим на b2x.
Например:
3⋅25х - 8⋅15х + 5⋅9х = 0 | : 9x
Слайд 14
Определение
Показательные неравенства –
это неравенства,
в которых неизвестное содержится в показателе степени.
Примеры:
Слайд 15
Простейшие показательные неравенства – это неравенства вида:
где a
> 0, a ≠ 1, b – любое число.
Слайд 16
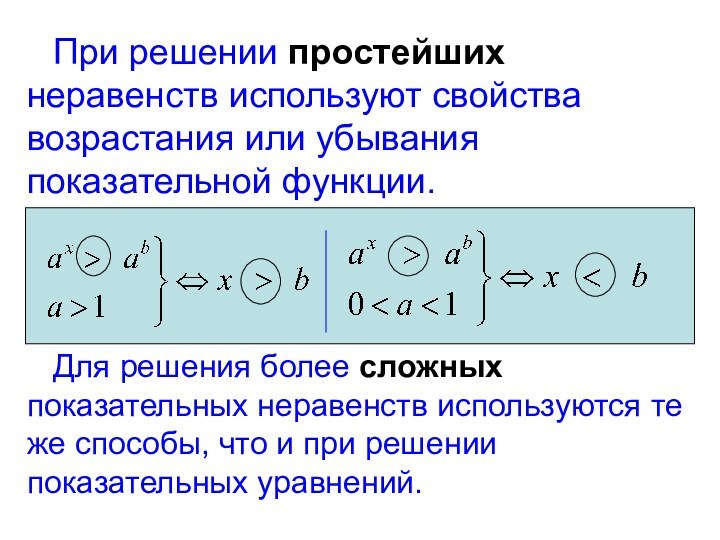
При решении простейших неравенств используют свойства
возрастания или убывания показательной функции.
Для решения более
сложных показательных неравенств используются те же способы, что и при решении показательных уравнений.
Слайд 17
Показательная функция
Построение графика
Сравнение чисел с использованием свойств
показательной функции
Сравнение числа с 1
а) аналитический способ;б) графический способ.
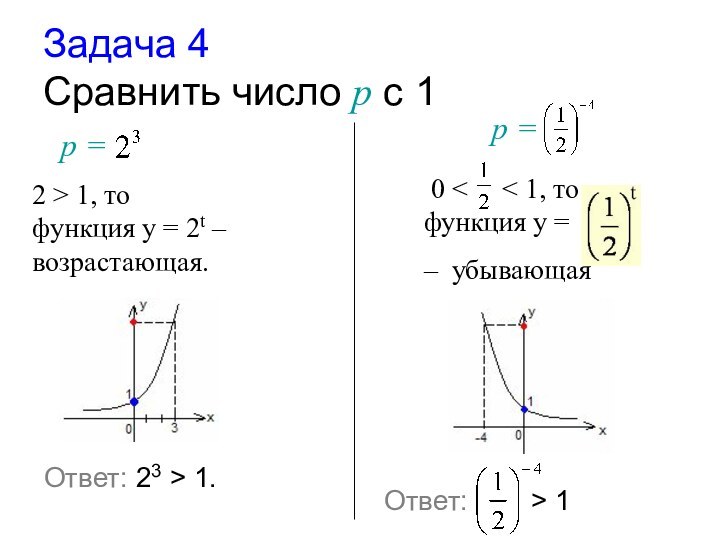
Слайд 21 Задача 4 Cравнить число р с 1
р =
2 > 1, то
функция у = 2t
– возрастающая. 0 < < 1, то
функция у =
– убывающая
Ответ: 23 > 1.
Ответ:
> 1
р =
Слайд 22
Решение показательных уравнений
Простейшие показательные уравнения
Уравнения, решаемые вынесением
за скобки степени с меньшим показателем
Уравнения, решаемые заменой переменной
случай 1; случай 2.
Уравнения, решаемые делением на показательную функцию случай 1;
случай 2.
Слайд 24
Вынесение за скобки степени с меньшим показателем
Ответ: 5
x
+ 1 - (x - 2) =
= x +
1 – x + 2 = 3
Слайд 25
Замена переменной (1)
основания степеней одинаковы, показатель одной из
степеней в 2 раза больше, чем у другой .
3
2x – 4 · 3 х – 45 = 0 t = 3x (t > 0)
t 2 – 4t – 45 = 0
По т. Виета: t1· t 2 = - 45; t1+ t 2 =4
t1 = 9; t 2 = - 5 – не удовлетворяет условию
3x = 9; 3x = 32; x = 2.
Ответ: 2
Слайд 26
Замена переменной (2)
Основания степеней одинаковы,
коэффициенты перед переменной
противоположны.
По т. Виета:
- Не удовлетворяет условию
Ответ: 1
Слайд 29
Простейшие показательные неравенства
Двойные неравенства
Неравенства, решаемые вынесением за скобки
степени с меньшим показателем
Неравенства, решаемые заменой переменной
Решение показательных неравенств
Слайд 32
Решение
показательных неравенств
Метод: Вынесение за скобки степени с
меньшим
показателем
Ответ: х
>3Т.к.
3 > 1, то знак неравенства остается прежним
: 10





























