Слайд 2
Учитель математики
Маеренкова Вера Васильевна
ПОСТРОЕНИЕ
И ПРЕОБРАЗОВАНИЕ
ГРАФИКОВ
КВАДРАТИЧНОЙ
ФУНКЦИИ
Слайд 3
Цели урока:
Образовательные:
экспериментальным путем получить алгоритмы построения графиков
функций видов у=а(х-т)2, у=ах2+n, у=а(х-т)2+n , если известен график
функции y=ах2;
научиться применять полученные алгоритмы к построению графиков функций.
Развивающие:
способствовать индивидуализации и дифференциации обучения с помощью применения информационно-коммуникационных технологий на уроках;
развивать у учащихся логическое мышление, внимание; формировать потребность в приобретении знаний
Воспитательные:
воспитывать навыки самоконтроля, привычки к рефлексии;
добиваться изменения роли ученика в учебном процессе от пассивного наблюдателя до активного исследователя.
Слайд 4
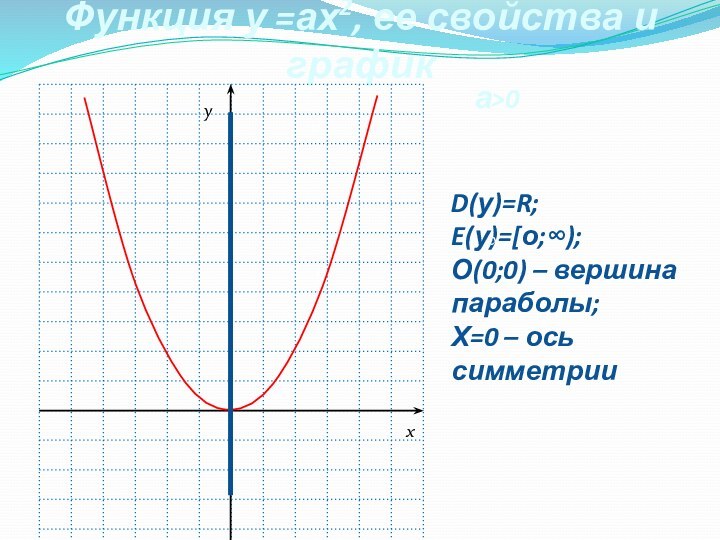
Функция у =ах2, ее свойства и график
D(у)=R;
E(у)=[о;∞);
О(0;0) – вершина параболы;
Х=0 – ось
симметрии
О
у
а>0
х
x
y
Слайд 5
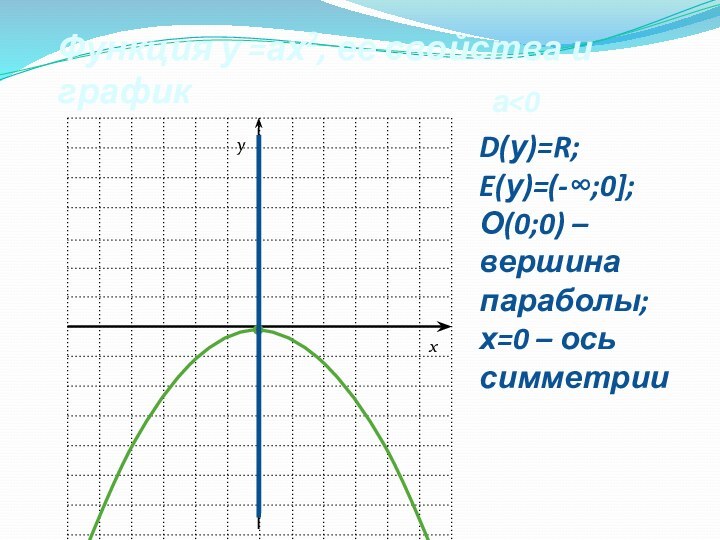
Функция у =ах2, ее свойства и график
а
вершина параболы;
х=0 – ось симметрии
x
y
Слайд 6
Функция у =ах2+n, ее свойства
и график
Графиком функции
у=ах2+n является парабола, которую можно получить из графика функции
у =ах2 с помощью параллельного переноса вдоль оси у на n единиц вверх, если n>0, или на –n единиц вниз, если n<0
Слайд 7
Функция у =ах2+n, ее свойства и график
x
y
Слайд 8
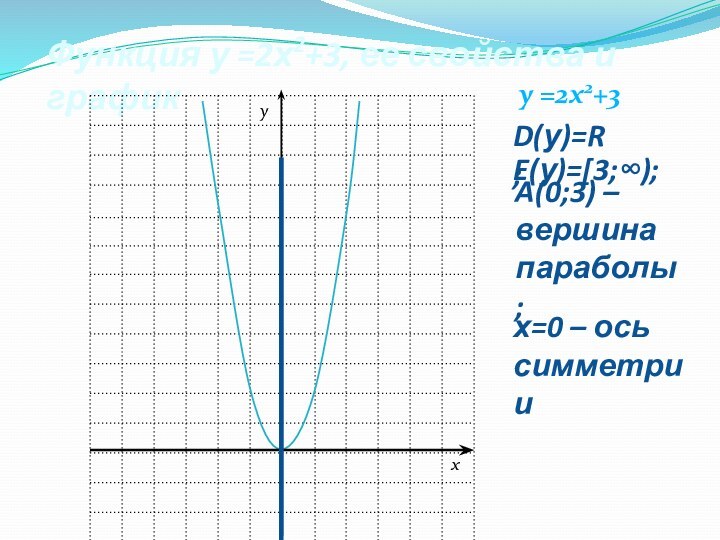
Функция у =2х2+3, ее свойства и график
A(0;3) –
вершина
параболы;
А
О
у
D(у)=R;
E(у)=[3;∞);
х=0 – ось
симметрии
у =2х2+3
x
y
Слайд 9
Функция у =ах2+n, ее свойства и график
D(у)=R;
E(у)=(-∞;
-3];
В(0;-3) – вершина параболы;
y=-¼x²-3
х=0 – ось
симметрии
x
y
Слайд 10
Графиком функции у = а (х - т)2
является парабола, которую можно получить из графика функции у
= ах2 с помощью параллельного переноса вдоль оси х на т единиц вправо, если т>0, или на –т единиц влево, если т<0
Слайд 11
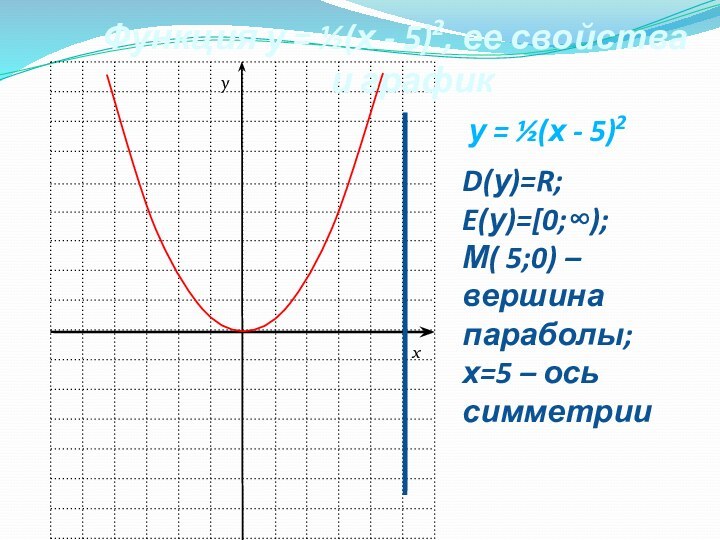
Функция у = ½(х - 5)2, ее свойства
и график
D(у)=R;
E(у)=[0;∞);
М( 5;0) –
вершина параболы;
х=5 – ось
симметрии
у = ½(х - 5)2
x
y
Слайд 12
y
x
y=-¼(x+5)²
Функция у = -¼ (х+5)2, ее свойства
и
график
D(у)=R; E(у)=(-∞;0];
М(-5;0)- вершина параболы;
Х=-5 – ось симметрии
Слайд 13
Графиком функции у = а (х - т)2
+ n является парабола, которую можно получить из графика
функции у = ах2 с помощью двух параллельных переносов: сдвига вдоль оси х на т единиц вправо, если т>0, или на – т единиц влево, если т<0, и сдвига вдоль оси у на n единиц вверх, если n >0, или на – n единиц вниз, если n <0
Слайд 14
y=-¼(x+2)²+4
Функция у=-¼(х+2)2+4, ее свойства и график
D(у)=R;
E(у)=(-∞;4];
М(-2;4)- вершина
параболы;
х=-2 – ось симметрии
x
y
Слайд 15
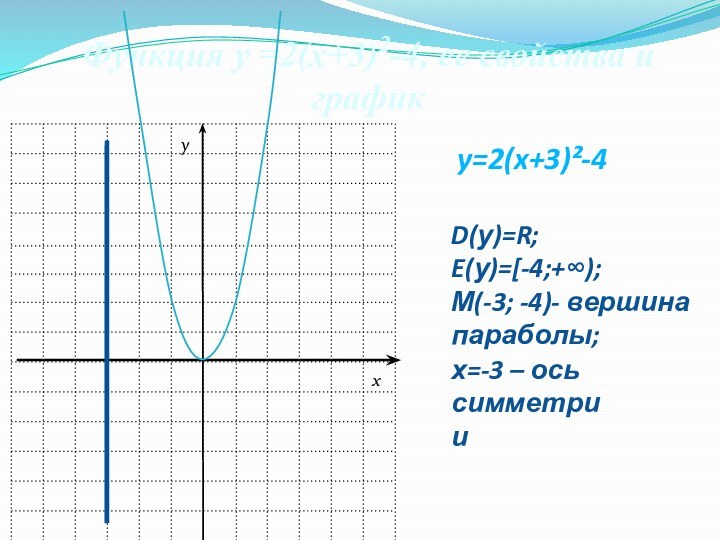
y=2(x+3)²-4
Функция у =2(х+3)2-4, ее свойства и график
D(у)=R;
E(у)=[-4;+∞);
М(-3; -4)- вершина параболы;
х=-3 – ось
симметрии
x
y
Слайд 16
Квадратичной функцией называется функция, которую можно задать формулой
вида
у =ах2 + вх + с,
где х
- независимая переменная,
а, в, и с -некоторые числа,
причем а ≠ 0.
Графиком функции является парабола
Слайд 17
Графиком функции у=ах2+вх+с
является парабола, вершина которой есть точка
(т; n), где
т=-b/2a
n = у(т)
Слайд 18
Осью симметрии параболы служит прямая
х = т,
параллельная оси у.
При а>0 ветви параболы направлены вверх,
а при
а < 0 – вниз
Слайд 19
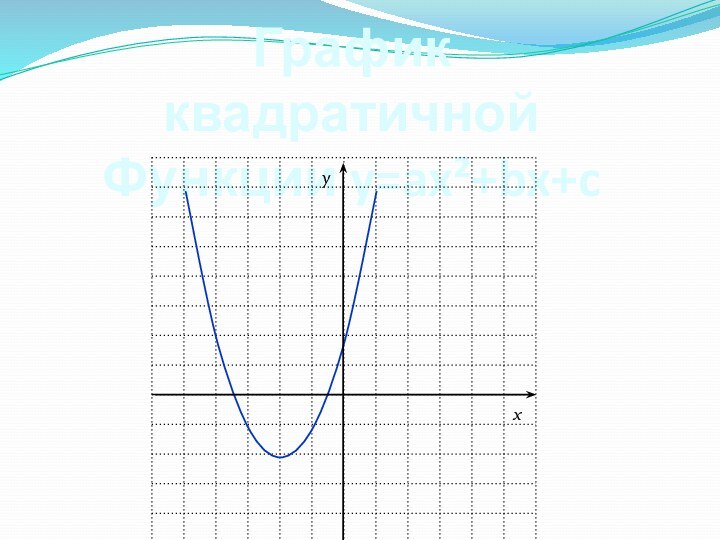
График квадратичной
Функции y=ax²+bx+c
x
y
Слайд 20
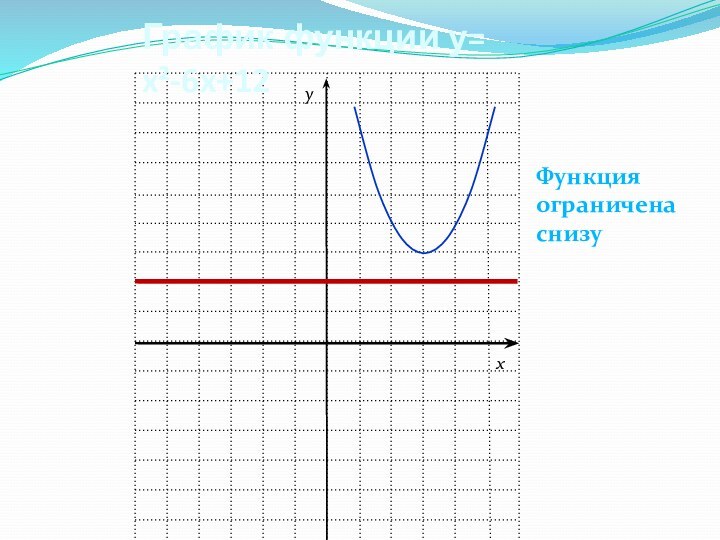
График функции у= x²-6x+12
x
y
Функция ограничена снизу
Слайд 21
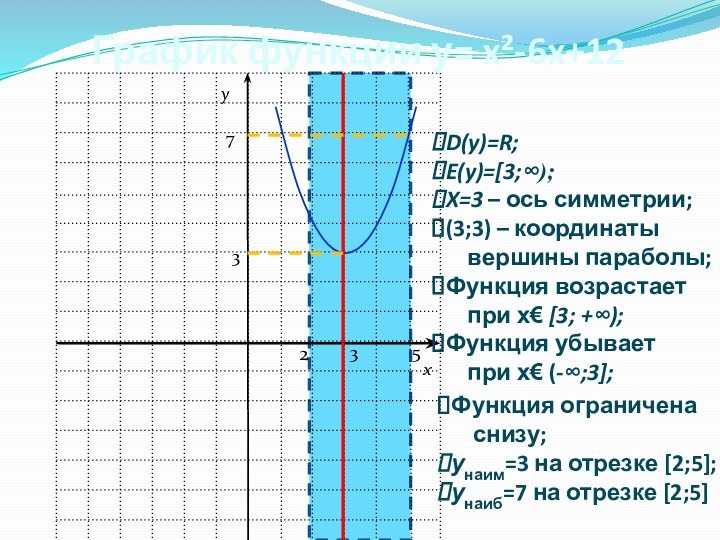
График функции у= x²-6x+12
D(y)=R;
E(y)=[3;∞);
X=3 – ось симметрии;
(3;3) –
координаты
вершины параболы;
Функция возрастает
при х€ [3;
+∞);
Функция убывает
при х€ (-∞;3];
Функция ограничена
снизу;
унаим=3 на отрезке [2;5];
унаиб=7 на отрезке [2;5]
3
3
7
5
2
x
y
Слайд 22
Итог урока
отмечаются лучшие работы;
проводится анализ работ учащихся;
организуется самооценка
учениками
своей деятельности;
фиксируется степень соответствия
поставленной цели
и результатов
деятельности;
намечаются цели последующей
деятельности;
комментируется домашнее задание.
Слайд 23
Домашнее задание
Построить графики функций и
описать их свойства:
y=2x2+4;
y=2(x+3)2-5;
y=1/2(x-6)2;
y=-3 x 2-6x+1.




![ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ Функция у =ах2+n, ее свойства и графикD(у)=R; E(у)=(-∞; -3];В(0;-3) – вершина параболы;y=-¼x²-3х=0 – ось симметрииxy](/img/tmb/14/1395807/989182c76bbebd95a8453e210273ed02-720x.jpg)

![ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ yxy=-¼(x+5)²Функция у = -¼ (х+5)2, ее свойства и графикD(у)=R; E(у)=(-∞;0];М(-5;0)-](/img/tmb/14/1395807/6b1b244160db44948c16c1d157c5a0e1-720x.jpg)

![ПОСТРОЕНИЕ И ПРЕОБРАЗОВАНИЕ ГРАФИКОВ КВАДРАТИЧНОЙ ФУНКЦИИ y=-¼(x+2)²+4Функция у=-¼(х+2)2+4, ее свойства и графикD(у)=R; E(у)=(-∞;4];](/img/tmb/14/1395807/daaec3079ca6d6f2e5d69f9f755d6707-720x.jpg)