Слайд 2
Дидактические принципы программы Л. В. Занкова:
обучение на высоком
уровне трудности;
изучение материала быстрым темпом;
ведущая роль
теоретических знаний;
осознание процесса учения школьниками;
работа над развитием всех учащихся, как слабых так и сильных.
Слайд 3
Главная задача обучения по системе Л. В. Занкова:
«…общее
развитие учащихся, которое понимается как развитие ума, воли, чувств
школьников и как надежная основа усвоения ими знаний, умений и навыков».
Слайд 4
Работа с текстом:
определить, является ли предложенный текст задачей;
выделить
в нем основные признаки этого вида заданий и ее
составные элементы;
установить между ними связи;
определить количество действий, необходимых для получения ответа на вопрос задачи;
выбирать действия и их порядок, обосновав свой выбор.
Слайд 5
И. И. Аргинская считает,
«…школа должна формировать у
детей истинное умение решать задачи, которое заключается в способности
решить любую задачу, доступного для данного возраста уровня трудности, если в ней отсутствуют незнакомые понятия и если для решения не требуется выполнить незнакомые операции…»
Слайд 6
Условия реализации развивающей функции при решении задач:
в задачах
должны быть отражены сложные, не «самоочевидные» ситуации, поэтому предлагаются
трудные, сложные задачи;
для рассмотрения сложной ситуации учащимся необходимо овладеть такими умениями, которые позволяют решить задачу определенной степени сложности (общие умения).
Слайд 7
Причины позднего введения термина «задача»:
необходимо, чтобы каждый ребенок
научился читать;
уровень развития мышления ребенка должен быть таков, чтобы
ребенок смог осмыслить текст и перевести его в знакомую модель;
учащиеся должны усвоить смысл действия сложения и вычитания;
у учащихся должен быть накоплен опыт работы с текстом математического содержания.
Слайд 8
Нетиповые (нестандартные) задачи – это задачи, для получения
ответа в которых арифметические действия или не выполняются вообще,
или выполняются в минимальном количестве.
с недостающими и избыточными данными;
с противоречивыми условием и вопросом;
логические задачи (не требуют арифметических действий);
комбинаторные.
Слайд 9
Комбинаторика-
это область математики, в которой изучаются
вопросы, связанные с выбором из некоторого множества подмножеств, обладающих
теми или иными свойствами, и упорядочением множества.
Слайд 10
Цель обучения решению КЗ-
развитие такого качества мышления,
как вариативность.
Слайд 11
Вариативность мышления-
направленность мыслительной деятельности ученика на поиск различных
решений задачи в случае, когда нет специального указания на
это.
Слайд 12
Методы решения КЗ:
«формальные»;
«неформальные».
Слайд 13
«Формальный» метод:
определяется характер выбора;
выбирается соответствующая формула или комбинаторное
правило;
подставляются числа и вычисляется результат ( результат - это
количество возможных вариантов, сами же варианты в этом случае не образовываются).
Слайд 14
«Неформальный» метод:
на первом плане сам процесс составления различных
вариантов;
главное не сколько, а какие варианты могут получиться.
Слайд 15
Группы комбинаторных задач разные по сложности осуществления перебора:
задачи,
в которых нужно произвести полный перебор всех возможных вариантов;
задачи,
в которых использовать прием полного перебора не целесообразно и нужно сразу исключить некоторые варианты, не рассматривая их (т. е. осуществить сокращенный перебор);
задачи, в которых операция перебора производится несколько раз и по отношению к разного рода объектам.
Слайд 16
Специфика методики:
способы действия не даются «в готовом виде»,
а дети сами приходят к их «открытию», накапливается опыт;
разнообразие
КЗ и различные решения их обеспечивает ученику выбор путей и средств решения в соответствии с его индивидуальными особенностями;
соблюдается этапность;
основное направление работы- переход от случайного перебора вариантов к систематическому.
Слайд 17
Этапы в обучении решению КЗ:
Подготовительный.
Системного перебора.
Решение задач
с помощью таблиц и графов.
Слайд 18
Примеры задач первого этапа:
Скажи, из каких фигур составлен
первый домик (рис. 1). Дорисуй второй домик так, чтобы
изменился порядок расположения фигур. Дорисуй третий домик так, чтобы изменился набор используемых фигур. Раскрась домики так, чтобы они отличались по цвету друг от друга.
Слайд 19
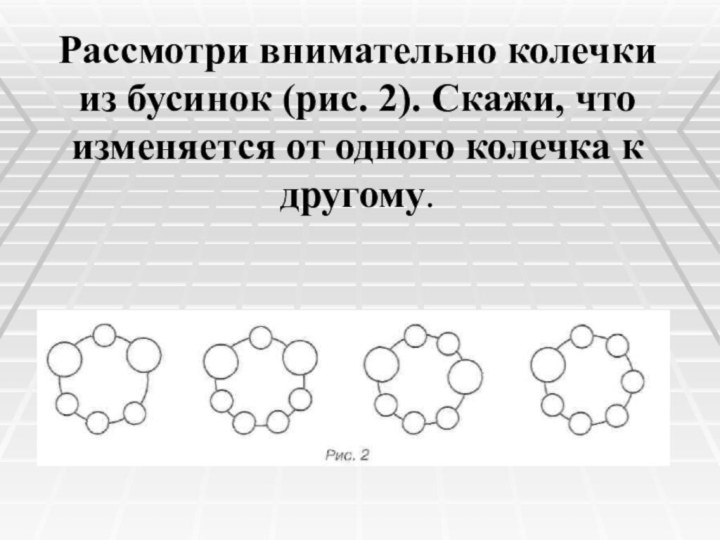
Рассмотри внимательно колечки из бусинок (рис. 2). Скажи,
что изменяется от одного колечка к другому.
Слайд 20
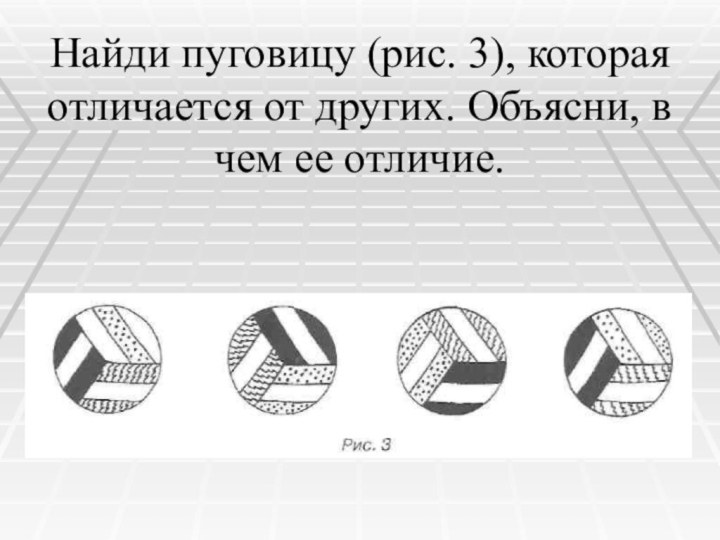
Найди пуговицу (рис. 3), которая отличается от других.
Объясни, в чем ее отличие.
Слайд 21
Цель работы на втором этапе:
Обучение школьников решению комбинаторных
задач с использованием систематического перебора всех возможных вариантов.
М.Ш.У Ш.У. М. У.
М.Ш.
М.У. Ш. Ш. М.У. У. Ш.М.
Слайд 22
Ориентировка на сидящего посередине или у прохода:
Ш.М. У М.Ш.У
М.У. Ш.
У М. Ш. У. Ш.М. Ш.У. М.
Ш. М.У.
М.У. Ш. У.Ш. М
М.Ш. У. У. М. Ш. Ш. У. М.
Слайд 23
Решение задач с помощью таблиц и графов:
Слайд 24
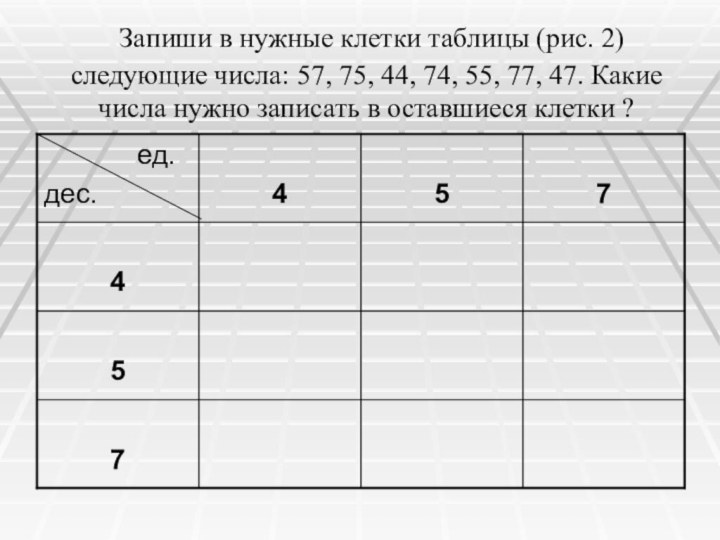
Запиши в нужные клетки таблицы (рис. 2)
следующие числа: 57, 75, 44, 74, 55, 77, 47.
Какие числа нужно записать в оставшиеся клетки ?
Слайд 25
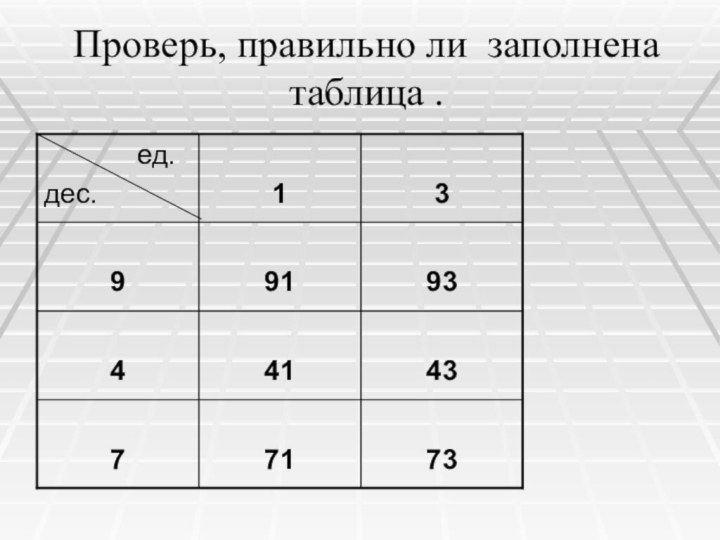
Проверь, правильно ли заполнена таблица .
Слайд 26
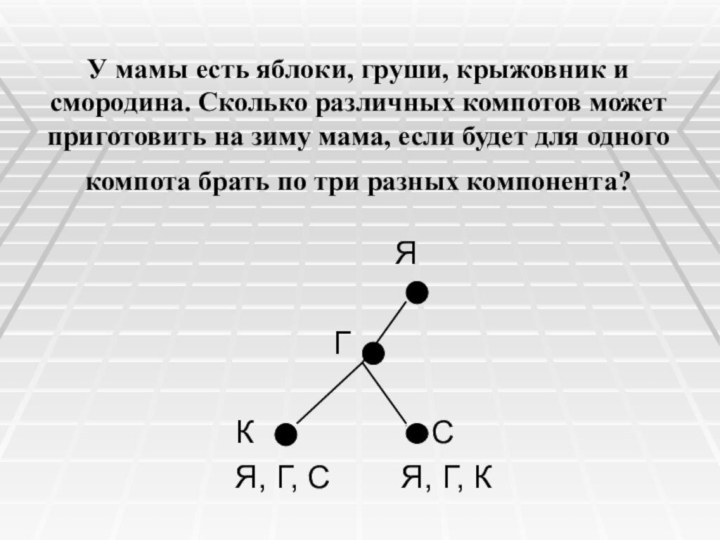
У мамы есть яблоки, груши, крыжовник и смородина.
Сколько различных компотов может приготовить на зиму мама, если
будет для одного компота брать по три разных компонента?
Я
Г
К С
Я, Г, С Я, Г, К
Слайд 27
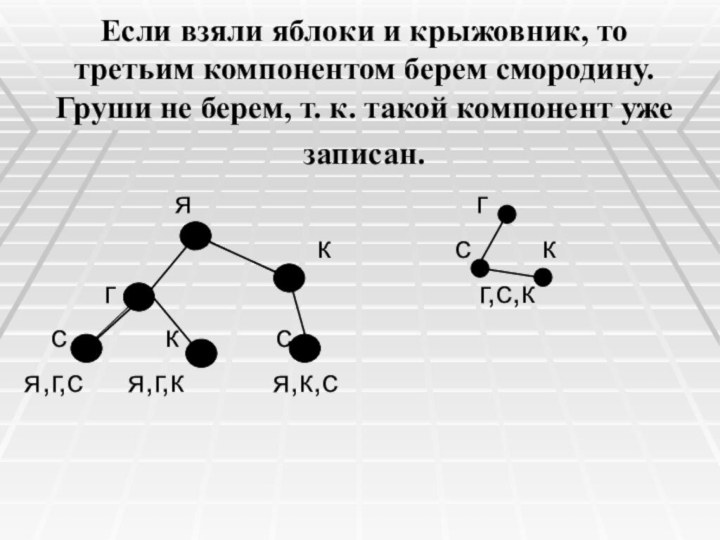
Если взяли яблоки и крыжовник, то третьим компонентом
берем смородину. Груши не берем, т. к. такой компонент
уже записан.
я г
к с к
г г,с,к
с к с
я,г,с я,г,к я,к,с