Слайд 2
Тема, её актуальность и цель исследования
Тема: способы решений
квадратных уравнений.
Актуальность: на уроках алгебры, геометрии, физики
мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, это также может мне пригодится при решении более сложных задач, в том числе и в 9 классе при сдаче экзаменов.
Цель работы: изучить различные методы решения квадратного уравнения и выявить наиболее легкий и быстрый способ.
Слайд 3
Задачи и гипотеза
Задачи:
- изучить историю развития квадратных уравнений;
-
рассмотреть стандартные и нестандартные методы решения квадратных уравнений;
-
выявить наиболее удобные способы решения квадратных уравнений;
- научиться решать квадратные уравнения различными способами.
Гипотеза: существует множество способов решения квадратных уравнений.
Слайд 4
Методы исследования
Методы исследования:
Теоретические: изучение литературы по теме исследования.
Анализ: информации полученной при изучении литературы; результатов полученных при
решении квадратных уравнений различными способами.
Сравнение способов на рациональность их использования при решении квадратных уравнений.
Слайд 5
Квадратные уравнения в древнем вавилоне
ax2+bx+c=0
Слайд 6
Квадратные уравнения в греции
В «Арифметике» Диофанта нет
систематического изложения алгебры, однако в ней содержится систематизированный ряд
задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение - 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 - х. Разность между ними 2х.
Отсюда уравнение:
(10 + х)(10 - х) = 96
100 - х2 = 96
х2 - 4 = 0
Отсюда х = 2, х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Слайд 7
Квадратные уравнения в индии
Слайд 8
Квадратные уравнения в европе в 13-17 веках
В Европе

были впервые изложены в «Книге абака», написанной в 1202
г. итальянским математиком Леонардо Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI - XVII вв. и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду:
х2 + bx = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Слайд 9
Квадратные уравнения
Квадра́тное уравне́ние — алгебраическое уравнение общего вида
ax2
+ bx + c = 0,
где x — свободная
переменная, a, b, c — коэффициенты, причём а=0.
Выражение ax2+bx+c называют квадратным трёхчленом.
Корень — это значение переменной x, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.
Элементы квадратного уравнения имеют собственные названия:
a называют первым или старшим коэффициентом,
b называют вторым или коэффициентом при x,
c называют свободным членом.
Слайд 12
Способ 2
Метод выделения полного квадрата
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
x2-10x+16=0
x2-2*5x+25-25+16=0
(x-5)2-9=0
(x-5)2=9
x-5=-3;x-5=3
x1=2 x2=8
Ответ:x1=2 ,x2=8
Слайд 15
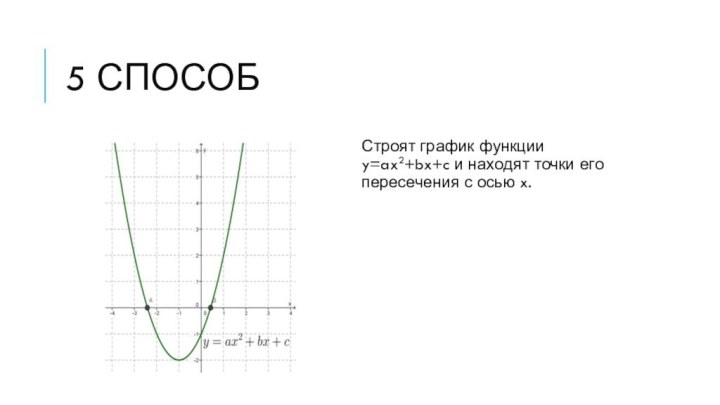
5 способ
Строят график функции y=ax2+bx+c и находят точки
его пересечения с осью x.
Слайд 16
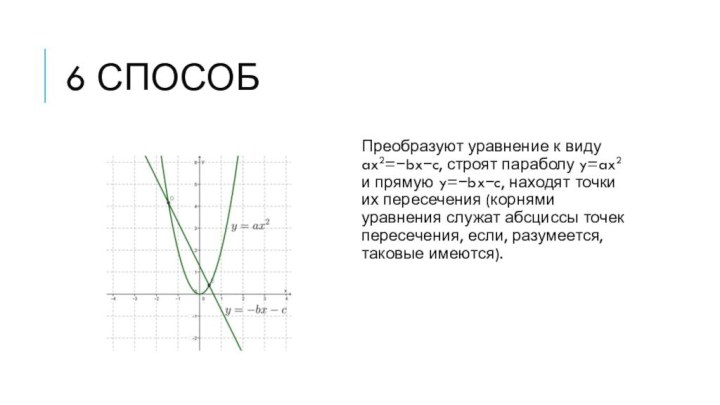
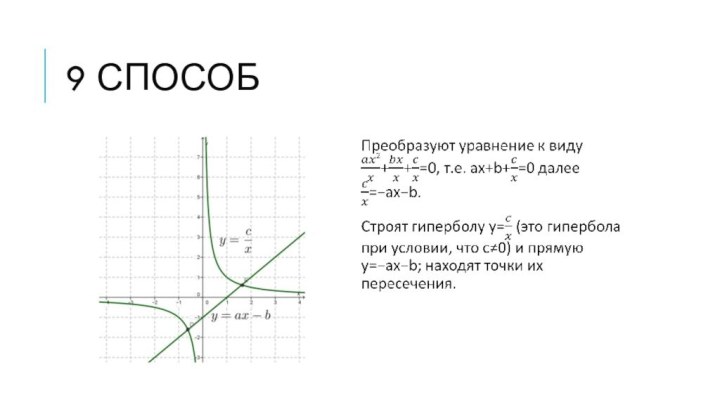
6 способ
Преобразуют уравнение к виду ax2=−bx−c, строят параболу
y=ax2 и прямую y=−bx−c, находят точки их пересечения (корнями
уравнения служат абсциссы точек пересечения, если, разумеется, таковые имеются).
Слайд 17
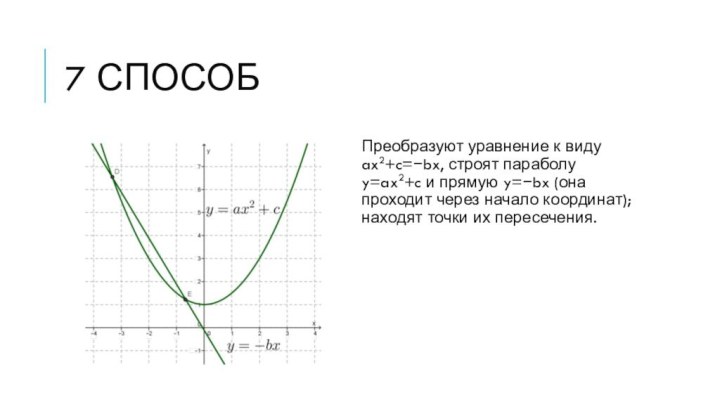
7 способ
Преобразуют уравнение к виду ax2+c=−bx, строят параболу
y=ax2+c и прямую y=−bx (она проходит через начало координат);
находят точки их пересечения.
Слайд 18
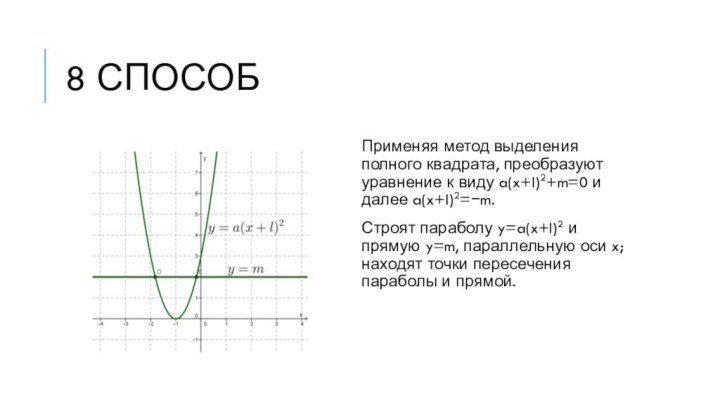
8 способ
Применяя метод выделения полного квадрата, преобразуют уравнение
к виду a(x+l)2+m=0 и далее a(x+l)2=−m.
Строят параболу y=a(x+l)2 и
прямую y=m, параллельную оси x; находят точки пересечения параболы и прямой.
Слайд 20
Франсуа виет
Франсуа́ Вие́т, сеньор де ля Биготье— французский
математик, основоположник символической алгебры.
Слайд 22
10 способ
Как известно, приведенное квадратное уравнение имеет вид
х2
+ px + c = 0.
Его корни удовлетворяют
теореме Виета, которая при а =1 имеет вид
x1*x2 = q,
x1 + x2 = - p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например,
x2 -3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = - 3 < 0;
x2+8x + 7 = 0; x1 =-7 и x2 =-1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q< 0 ).
Например,
x2 + 4x- 5 = 0; x1 = - 5 и x2 = 1, так как q= - 5< 0;
x2- 8x- 9 = 0; x1 = 9 и x2 = - 1, так как q = - 9 < 0 и p = - 8 < 0.