Презентация на тему по математике на тему Числовые ряды (2 курс СПО)

Содержание

2. Цель урока:Обеспечение усвоения понятия числового ряда, его
3. Числовым рядом называется сумма вида:где числа u1,
4. Если
5. Пример.Найти сумму членов ряда:Находим частичные суммы членов ряда:
6. Запишем последовательность частичных сумм:
7. Необходимый признак сходимости рядаРяд
8. Достаточные признаки сходимости ряда с положительными членамиа)
9. образован из членов геометрической прогрессии:Геометрический рядсходится при |q|
10. Обобщенный гармонический рядсходится при p >1расходится при p ≤1
11. Пример. Исследовать сходимость ряда, применяя необходимый признак
12. Сравнивая члены нашего ряда с соответствующими членами
13. Скачать презентацию
14. Похожие презентации

Цель урока:Обеспечение усвоения понятия числового ряда, его суммы, сходящегося и расходящегося рядов. Формирование представлений о признаках сходимости ряда.Формирование умений исследования сходимости ряда.

Главная
Математика
Презентация по математике на тему Числовые ряды (2 курс СПО)

Числовые ряды. Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.

Цель урока:Обеспечение усвоения понятия числового ряда, его суммы, сходящегося и расходящегося рядов.

Числовым рядом называется сумма вида:где числа u1, u2, u3,…,un,... – члены ряда

Пример.Найти сумму членов ряда:Находим частичные суммы членов ряда:

Запишем последовательность частичных сумм:

Необходимый признак сходимости рядаРяд может сходиться только

Достаточные признаки сходимости ряда с положительными членамиа) Признак сравнения рядов с положительными

образован из членов геометрической прогрессии:Геометрический рядсходится при |q|

Обобщенный гармонический рядсходится при p >1расходится при p ≤1

Пример. Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения:Необходимый признак

Сравнивая члены нашего ряда с соответствующими членами геометрического ряда, получим неравенства:Т.е. члены

Пример. Исследовать сходимость ряда, используя признак Даламбера:Следовательно, данный ряд сходится.

Слайды презентации

Слайд 2 Цель урока:
Обеспечение усвоения понятия числового ряда, его суммы,

Цель урока:Обеспечение усвоения понятия числового ряда, его суммы, сходящегося и расходящегося

сходящегося и расходящегося рядов.
Формирование представлений о признаках сходимости

ряда.
Формирование умений исследования сходимости ряда.

Слайд 3 Числовым рядом называется сумма вида:
где числа u1, u2,

Числовым рядом называется сумма вида:где числа u1, u2, u3,…,un,... – члены

u3,…,un,... – члены ряда (бесконечная последовательность),
un – общий член

ряда.

Частичные суммы ряда:
S1=u1,
S2=u1+u2,
S3=u1+u2+u3,
…………………..
Sn=u1+u2+u3+…+un

Слайд 4 Если

или

,

то ряд называется сходящимся, а число S – суммой сходящегося ряда.

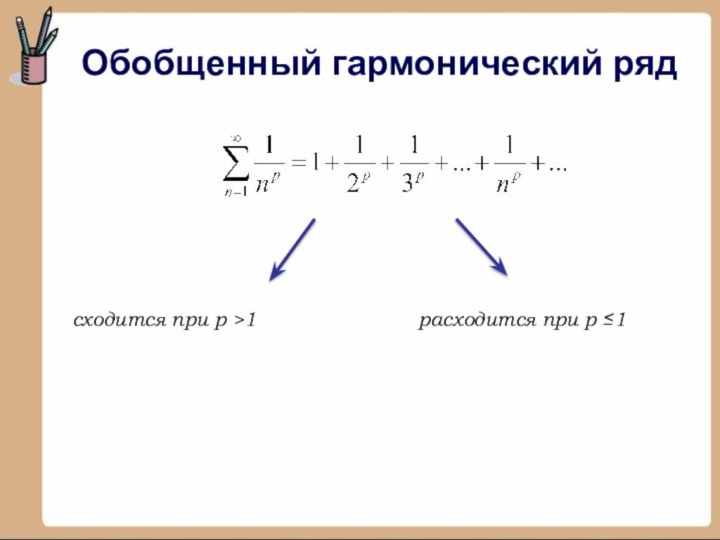
Если частичная сумма Sn ряда при неограниченном возрастании n не имеет конечного предела (в частности, стремится к +∞ или к -∞), то такой ряд называется расходящимся.

Слайд 5 Пример.
Найти сумму членов ряда:
Находим частичные суммы членов ряда:

Слайд 6 Запишем последовательность частичных сумм:

Запишем последовательность частичных сумм: …Общий член

…
Общий член этой

последовательности есть: n/(2n+1)

Последовательность частичных сумм имеет предел, равный 1/2. Итак, ряд сходится и его сумма равна 1/2.

Слайд 7 Необходимый признак сходимости ряда
Ряд

Необходимый признак сходимости рядаРяд может сходиться только при условии,

может сходиться только при условии, что его общий

член un при неограниченном увеличении номера n стремится к нулю:

Если , то ряд расходится – это достаточный признак расходимости ряда.

Слайд 8 Достаточные признаки сходимости ряда с положительными членами
а) Признак

Достаточные признаки сходимости ряда с положительными членамиа) Признак сравнения рядов с

сравнения рядов с положительными членами.
Исследуемый ряд сходится, если

его члены не превосходят соответствующих членов другого, заведомо сходящегося ряда: исследуемый ряд расходится, если его члены превосходят соответствующие члены другого заведомо расходящегося ряда.

б) Признак Даламбера.
Если для ряда с положительными членами

выполняется условие , то ряд сходится при l<1 и расходится при l>1.
Признак Даламбера не дает ответа, если l=1. В этом случае для исследования ряда применяют другие приемы.