- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку алгебры по теме y=cos x@
Содержание
- 2. Тема: «Функция y = cos x, её свойства и график»
- 3. ПОВТОРЕНИЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЯ ФУНКЦИИФункция
- 4. ПОВТОРЕНИЕ ПЕРИОДИЧНОСТЬcos(x + 2π) = cos x,
- 5. ПОВТОРЕНИЕ ЧЁТНОСТЬ И НЕЧЁТНОСТЬ:cos (–x) =
- 6. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИo
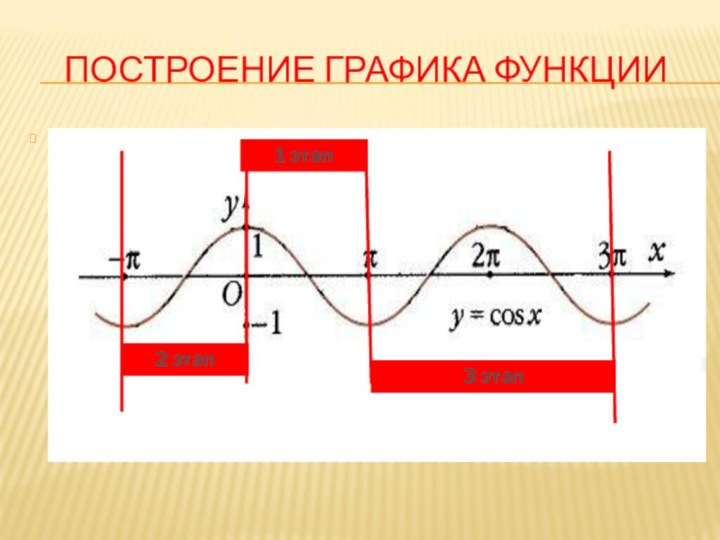
- 7. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
- 8. III IIIIY IIIIYIIIπ - шесть клетокОсь косинусовII
- 9. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ Y= COS X1.Область
- 10. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ Y= COS X2.
- 11. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ Y= COS X3.Функция у= cos x периодическая с периодом 2π
- 12. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ Y= COS X4.Функция y= cos x – четная
- 13. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ Y= COS X5.
- 14. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ Y= COS X6.
- 15. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ Y= COS X7.
- 16. ПРИМЕРЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВПример 1: найти
- 17. ПРИМЕРЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВГрафики заданных функций
- 18. ПРИМЕРЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВПример 2: найти
- 19. ПРИМЕРЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВПример 2: Найти
- 20. УПРАЖНЕНИЯ ( УСТНО)№ 708 Выяснить, при каких
- 21. УПРАЖНЕНИЯ ( УСТНО)№ 709 Выяснить ,
- 22. УПРАЖНЕНИЯ № 710 Разбить данный отрезок
- 23. УПРАЖНЕНИЯ № 710 Разбить данный отрезок
- 24. УПРАЖНЕНИЯ№ 711 Используя свойство возрастания или убывания
- 25. УПРАЖНЕНИЯ№ 711 Используя свойство возрастания или убывания
- 26. УПРАЖНЕНИЯ№712 Найти все корни уравнения, принадлежащие отрезку
- 27. УПРАЖНЕНИЯ№712 Найти все корни уравнения, принадлежащие отрезку
- 28. УПРАЖНЕНИЯ№712 Найти все корни уравнения, принадлежащие отрезку
- 29. УПРАЖНЕНИЯ№712 Найти все корни уравнения, принадлежащие отрезку
- 30. УПРАЖНЕНИЯ№ 713.Найти все решения неравенства, принадлежащие отрезку
- 31. УПРАЖНЕНИЯ№ 713.Найти все решения неравенства, принадлежащие отрезку
- 32. УПРАЖНЕНИЯ№ 713.Найти все решения неравенства, принадлежащие отрезку [0; 3π] :3) cos x
- 33. УПРАЖНЕНИЯ№ 713.Найти все решения неравенства, принадлежащие отрезку
- 34. УПРАЖНЕНИЯ№ 714 Выразите синус через косинус по
- 35. УПРАЖНЕНИЯ№ 714 Выразите синус через косинус по
- 36. УПРАЖНЕНИЯ№ 714 Выразите синус через косинус по
- 37. УПРАЖНЕНИЯ№ 715 Найти все корни уравнения, принадлежащие
- 38. УПРАЖНЕНИЯ№ 715 Найти все корни уравнения, принадлежащие
- 39. УПРАЖНЕНИЯ№ 716 Найти все решения неравенства ,
- 40. УПРАЖНЕНИЯ№ 716. Найти все корни уравнения, принадлежащие
- 41. УПРАЖНЕНИЯ№ 717 Построить график функции и выяснить
- 42. 2) Область значений функции - [ 0;
- 43. УПРАЖНЕНИЯ№ 718 Найти множество значений функции y=cos
- 44. Скачать презентацию
- 45. Похожие презентации
Тема: «Функция y = cos x, её свойства и график»



















![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№712 Найти все корни уравнения, принадлежащие отрезку [0; 3π] :1) cos x](/img/tmb/7/659634/9378c1cc5c0a12a95ac13955b81f7c78-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№712 Найти все корни уравнения, принадлежащие отрезку [0; 3π] :2) cos x](/img/tmb/7/659634/9594d08c4a6b9ef5f20f7f3cdc7672c2-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№712 Найти все корни уравнения, принадлежащие отрезку [0; 3π] :3) cos x=](/img/tmb/7/659634/88b14871afaf538a669e0e7fd1aee80e-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№712 Найти все корни уравнения, принадлежащие отрезку [0; 3π] :4) cos x](/img/tmb/7/659634/233cafdbc91e26ebdb4424f01bb7037d-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№ 713.Найти все решения неравенства, принадлежащие отрезку [0; 3π] :1) cos x](/img/tmb/7/659634/7c39d86fd8f5ec19a066139578cc1e5a-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№ 713.Найти все решения неравенства, принадлежащие отрезку [0; 3π] :2) cos x](/img/tmb/7/659634/d4cd4960948763f4b7ccd03a5de68aae-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№ 713.Найти все решения неравенства, принадлежащие отрезку [0; 3π] :3) cos x](/img/tmb/7/659634/244aacd6ce2a530e62421b5e0aed1d98-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№ 713.Найти все решения неравенства, принадлежащие отрезку [0; 3π] :4) cos x](/img/tmb/7/659634/a74fb184b665e209b5e5cbd7b26216d7-720x.jpg)



![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№ 715 Найти все корни уравнения, принадлежащие отрезку [ -π/2; 3π/2] :1)](/img/tmb/7/659634/7226a6e0745606ddb3e547453996daef-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№ 715 Найти все корни уравнения, принадлежащие отрезку [ -π/2; 3π/2] :2)](/img/tmb/7/659634/82114c97dce0a5d1e6572df036d9c69c-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№ 716 Найти все решения неравенства , принадлежащие отрезку [ -π/2; 3π/2]](/img/tmb/7/659634/2749710a97a3484ffff6ea52fe2c1f88-720x.jpg)
![Презентация к уроку алгебры по теме y=cos x@ УПРАЖНЕНИЯ№ 716. Найти все корни уравнения, принадлежащие отрезку [ -π/2; 3π/2] :2)](/img/tmb/7/659634/e1d0b47ae82a77fd212249817f39dcbb-720x.jpg)

![Презентация к уроку алгебры по теме y=cos x@ 2) Область значений функции - [ 0; 2] 3) Периодическая с периодом](/img/tmb/7/659634/10f93f6622f213b0882f44c99feb34c3-720x.jpg)


Слайд 3
ПОВТОРЕНИЕ
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ ЗНАЧЕНИЯ ФУНКЦИИ
Функция определена на
всей числовой прямой;
Множество значений функции – отрезок [- 1;
1]
Слайд 4
ПОВТОРЕНИЕ
ПЕРИОДИЧНОСТЬ
cos(x + 2π) = cos x,
Функция y=cos
x -периодическая с периодом 2π ( строим график на
промежутке длиной 2π , например [- π; π])
Слайд 5
ПОВТОРЕНИЕ
ЧЁТНОСТЬ И НЕЧЁТНОСТЬ:
cos (–x) = cos x,
Функция y=cos x является чётной (
график симметричен относительно оси OY , строим график на промежутке [0; π])
Слайд 6
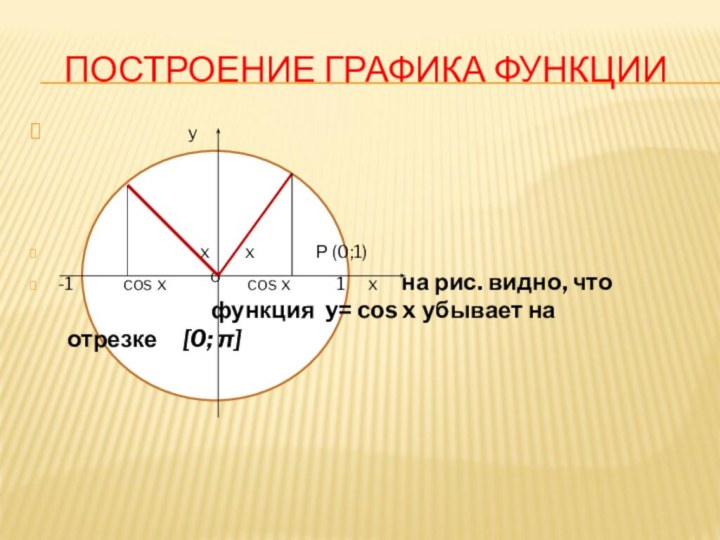
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
o
y
x x Р (0;1)
-1 cos x cos x 1 x на рис. видно, что функция y= cos x убывает на отрезке [0; π]
Слайд 8
III
II
I
IY
III
IY
I
II
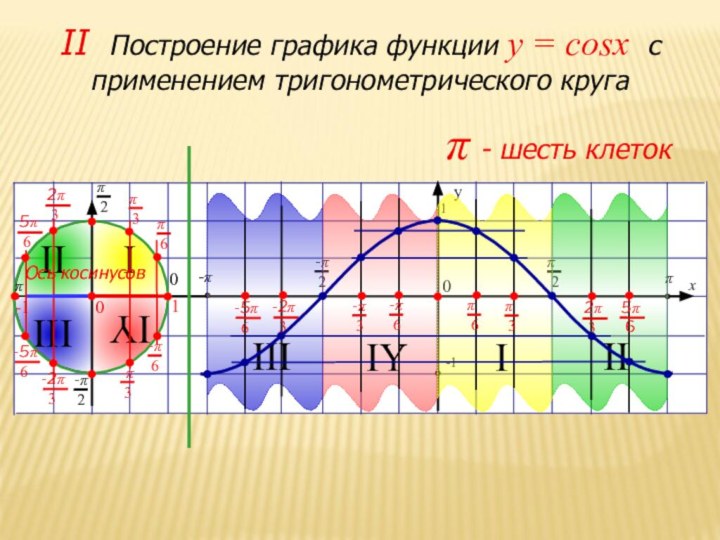
π - шесть клеток
Ось косинусов
II Построение
графика функции y = cosx с применением тригонометрического круга
Слайд 9
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ
Y= COS X
1.Область определения
–
множество R всех действительных чисел
yx
График расположен вдоль всей оси OX
Слайд 10
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ
Y= COS X
2. Множество значений
функции
1-1
График ограничен линиями У=-1 и У=1
Слайд 13
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ
Y= COS X
5. У=0 при
х= π/2 + πп, пє Z
Наибольшее значение у=1, если
х= 2 πп, пє ZНаименьшее значение у=-1, если х= Наибольшее значение у=1, если х= π+2 πп, пє Z
У>0 на интервале (-π/2 ; π/2 ) и на интервалах со сдвигом на 2 πп
У<0 на интервале (π/2 ; 3π/2 ) и на интервалах со сдвигом на 2 πп
Слайд 14
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ
Y= COS X
6. возрастает на
(π ; 2π ) и на интервалах , получаемых
сдвигами этого отрезка на 2 πп
Слайд 15
ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ
Y= COS X
7. убывает на
(0; π ) и на интервалах , получаемых сдвигами
этого отрезка на 2 πп
Слайд 16
ПРИМЕРЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВ
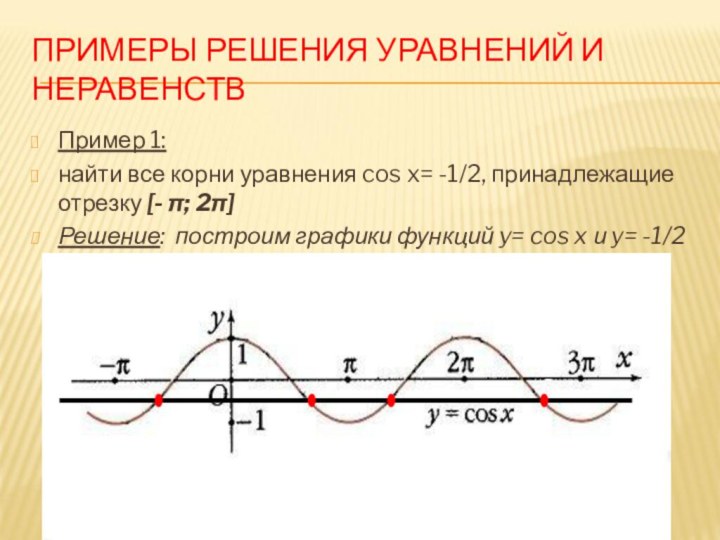
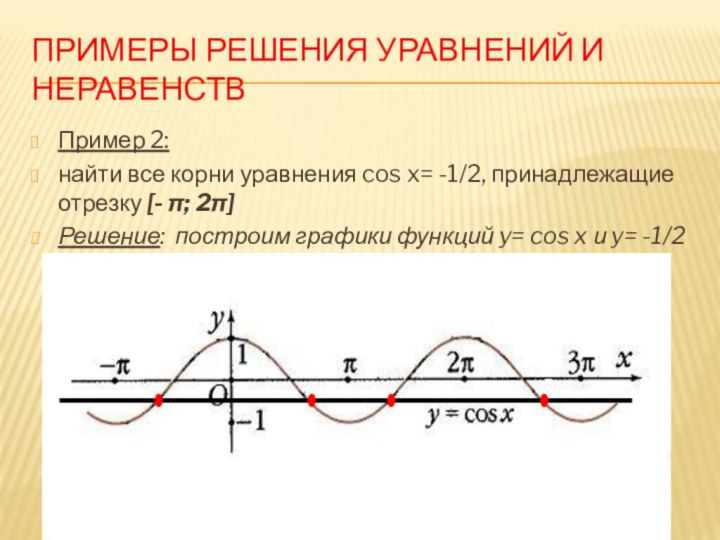
Пример 1:
найти все
корни уравнения cos x= -1/2, принадлежащие отрезку [- π;
2π]Решение: построим графики функций y= cos x и y= -1/2
Слайд 17
ПРИМЕРЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВ
Графики заданных функций пересекаются
в точках, отмеченных на графике:
Абсциссы этих точек являются решениями
данного уравненияНа отрезке [0; π] корнем уравнения cos x = -1/2 является число arccos (-1/2) = 2π/3.
Следующим решением является число, симметричное относительно оси ОУ: х= - 2π/3.
Третий корень уравнения равен :- 2π/3 + 2π= 4π/3
Ответ : 2π/3; - 2π/3; 4π/3
Слайд 18
ПРИМЕРЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВ
Пример 2:
найти все
корни уравнения cos x= -1/2, принадлежащие отрезку [- π;
2π]Решение: построим графики функций y= cos x и y= -1/2
Слайд 19
ПРИМЕРЫ РЕШЕНИЯ УРАВНЕНИЙ И НЕРАВЕНСТВ
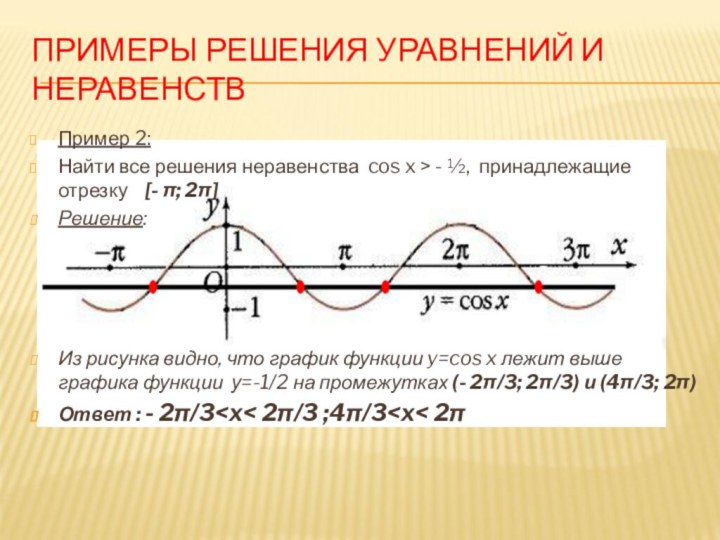
Пример 2:
Найти все
решения неравенства cos x > - ½, принадлежащие отрезку
[- π; 2π]Решение:
Из рисунка видно, что график функции y=cos x лежит выше графика функции у=-1/2 на промежутках (- 2π/3; 2π/3) и (4π/3; 2π)
Ответ : - 2π/3
Слайд 20
УПРАЖНЕНИЯ ( УСТНО)
№ 708 Выяснить, при каких значениях
х, принадлежащих отрезку [0; 3π], функция у=cos x принимает
:1)значение , равное 0
Ответ : π/2; 3π/2; 5π/2
2) значение, равное 1
Ответ : 0; 2π
3) значение , равное -1
Ответ : π; 2 π
4) положительные значения
Ответ: (0; π/2); (3π/2; 5π/2)
5) отрицательные значения
Ответ : (π/2; 3π/2) ; (5π/2; 3π )
Слайд 21
УПРАЖНЕНИЯ ( УСТНО)
№ 709 Выяснить , возрастает
или убывает функция y=cos x на отрезке:
1) [3π; 4π]
Ответ
: возрастает2) [- 2π; -π]
Ответ : убывает
3) [2 π; 5π/2]
Ответ : убывает
4) [- π/2; 0]
Ответ : возрастает
5) [1; 3]
Ответ: убывает
6) [- 2; -1]
Ответ : возрастает
Слайд 22
УПРАЖНЕНИЯ
№ 710 Разбить данный отрезок на
два так, чтобы на одном из них функция y=cos
x возрастала, а на другом убывала:1) ) [π/2; 3π/2]
Ответ : ) [π/2; π] и [π; 3π/2]
2) ) [- π/2; π/2]
Ответ: ) [-π/2; 0] и [ 0 ; π/2]
Слайд 23
УПРАЖНЕНИЯ
№ 710 Разбить данный отрезок на
два так, чтобы на одном из них функция y=cos
x возрастала, а на другом убывала:3) [0; 3π/2]
Ответ: ) [0; π] и [ π; 3π/2]
4) ) [- π; π/2]
Ответ : ) [- π; 0] ) [0 ; π/2]
Слайд 24
УПРАЖНЕНИЯ
№ 711 Используя свойство возрастания или убывания функции
y=cos x, сравнить числа:
1) cos π/7 и cos 8π/9
Ответ:
на интервале ( 0; π) функция убывает, значит т.к. π/7 < 8π/9, то ) cos π/7 > cos 8π/9
2) cos 8π/7 и cos 10π/7
Ответ: на интервале ( π; 2π ) функция возрастает, значит т.к.
8π/7 < 10π/7, то cos 8π/7
Ответ: на интервале (- π; 0 ) функция возрастает, значит т.к.
-6π/7 < -π/8, то cos (-6π/7)
Слайд 25
УПРАЖНЕНИЯ
№ 711 Используя свойство возрастания или убывания функции
y=cos x, сравнить числа:
4) cos(- 8π/7) и cos (-9π/7)
Ответ:
на интервале ( -3π/2; -π) функция убывает, значит т.к. -8π/7 > -9π/7, то cos(- 8π/7) < cos (-9π/7)
5) cos1 и cos 3
Ответ: на интервале ( 0; π) функция убывает, значит т.к.
1 < 3,то cos1 > cos 3
6) cos 4 и cos 5
Ответ: на интервале ( π; 2π) функция возрастает, значит т.к.
4< 5, то cos4 < cos 5
Слайд 26
УПРАЖНЕНИЯ
№712 Найти все корни уравнения, принадлежащие отрезку [0;
3π] :
1) cos x = ½
Решение : На отрезке
[0; π] корнем уравнения cos x = 1/2 является число х=arccos (1/2) = π/3, на промежутке [ π; 2π] - , х=π/3+ 3 π/2=11π/6, на промежутке [ 2π; 3π] - , х=π/3+ +2π=7π/3Ответ: х= π/3; х=11 π/6; х=7π/3
Слайд 27
УПРАЖНЕНИЯ
№712 Найти все корни уравнения, принадлежащие отрезку [0;
3π] :
2) cos x = /2
Решение : На
отрезке [0; π] корнем уравнения cos x = /2 является число х= arccos ( /2) = π/4 . На отрезке [ π; 2 π;] корнем уравнения cos x = /2 является число х = 7 π/4. На отрезке [ 2π; 3π;] корнем уравнения cos x = /2 является число х = π/4+2 π= 9π/4Ответ : х= π/4 ; х= 7π/4 ; х= 9π/4
Слайд 28
УПРАЖНЕНИЯ
№712 Найти все корни уравнения, принадлежащие отрезку [0;
3π] :
3) cos x= - /2
Решение
: На отрезке [0; π] корнем уравнения cos x =- /2 является число х= arccos ( - /2) = 3π/4 . На отрезке [ π; 2 π;] корнем уравнения cos x = /2 является число х = 5 π/4. На отрезке [ 2π; 3π;] корнем уравнения cos x = /2 является число х = 3 π/4+2 π= 11π/4Ответ : х=3π/4 ; х=5 π/4 ; х=11π/4
Слайд 29
УПРАЖНЕНИЯ
№712 Найти все корни уравнения, принадлежащие отрезку [0;
3π] :
4) cos x = - ½
Решение : На
отрезке [0; π] корнем уравнения cos x =- 1/2 является число х=arccos (-1/2) = 2π/3, на промежутке [ π; 2π] - , х=π/3+ π=4π/3, на промежутке [ 2π; 3π] - , х=2π/3+ +2π=8π/3Ответ: х= 2π/3; х=4π/3; х=8π/3
Слайд 30
УПРАЖНЕНИЯ
№ 713.Найти все решения неравенства, принадлежащие отрезку [0;
3π] :
1) cos x ≥ 1/2
Решение :
По рисунку
видно, что график функции y=cos x расположен выше графика функции у=1/2 на промежутках ([ 0; π/3 ] и [ 11 π/6; 7π/3 ] Ответ : [ 0; π/3 ] и [ 11 π/6; 7π/3 ]
Слайд 31
УПРАЖНЕНИЯ
№ 713.Найти все решения неравенства, принадлежащие отрезку [0;
3π] :
2) cos x ≥- 1/2
Решение :
По рисунку
видно, что график функции y=cos x расположен выше графика функции у=-1/2 на промежутках ([ 0;2π/3 ] и [ 4 π/3; 8π/3 ] Ответ : [ 0; 2π/3 ] и [ 4 π/3; 8π/3 ]
Слайд 32
УПРАЖНЕНИЯ
№ 713.Найти все решения неравенства, принадлежащие отрезку [0;
3π] :
3) cos x
рисунку видно, что график функции y=cos x расположен ниже графика функции у=- /2 на промежутках (3π/4;5π/4 ) и ( 11 π/4; 3π) Ответ : (3π/4;5π/4 ) и ( 11 π/4; 3π)
Слайд 33
УПРАЖНЕНИЯ
№ 713.Найти все решения неравенства, принадлежащие отрезку [0;
3π] :
4) cos x < /2
Решение :
По
рисунку видно, что график функции y=cos x расположен ниже графика функции у= /2 на промежутках ( 0; π/6 ) и (11 π/6; 13π/6 ) Ответ : ( 0; π/6 ) и (11 π/6; 13π/6 )
Слайд 34
УПРАЖНЕНИЯ
№ 714 Выразите синус через косинус по формулам
приведения , сравните числа:
1) cos π/5 и sin
π/5Решение: sin π/5= sin (π/2 - 3π/5)= cos 3π/10. Сравним cos π/5 и cos 3π/10; π/5 < 3π/10, значит cos π/5 > cos 3π/10, а значит cos π/5 > sin π/5
Ответ : cos π/5 > sin π/5
2) sin π/7 и cos π/7
Решение: sin π/7= sin (π/2 - π/7)= cos 5π/14. Сравним cos π/7 и cos 5π/14; π/7 < 5π/14, значит cos π/7 > cos 5π/14, а значит cos π/7 > sin π/7
Ответ : sin π/7
Слайд 35
УПРАЖНЕНИЯ
№ 714 Выразите синус через косинус по формулам
приведения , сравните числа:
3) cos 3π/8 и sin
5π/8Решение: sin 5π/8= sin (π/2 + π/8)= cos π/8. Сравним cos 3π/8 и cos π/8; π/8 < 3π/8, значит cos 3π/8 < cos π/8, а значит cos 3π/8 < sin 5π/8
Ответ : cos 3π/8 < sin 5π/8
4) sin 3π/5 и cos π/5
Решение: sin 3π/5= sin (π/2 + π/10)= cos π/10. Сравним cos 3π/5 и cos π/10; 3π/5 > π/10, значит cos 3π/5 < cos π/10, а значит sin 3π/5< cos π/5
Ответ : sin 3π/5< cos π/5
Слайд 36
УПРАЖНЕНИЯ
№ 714 Выразите синус через косинус по формулам
приведения , сравните числа:
5) cos π/6 и sin
5π/14Решение: sin 5π/14= sin (π/2 - π/7)= cos π/7. Сравним cos π/6 и cos π/7; π/6 > π/7, значит cos π/6 < cos π/7, а значит cos π/6 < sin 5π/14
Ответ : cos π/6 < sin 5π/14
6) cos π/8 и sin 3π/10
Решение: sin 3π/10= sin (π/2 - π/5)= cos π/5. Сравним cos π/8 и cos π/5; π/8 < π/5, значит cos π/8 > cos π/5, а значит cos π/8 > sin 3π/10
Ответ : cos π/8 > sin 3π/10
Слайд 37
УПРАЖНЕНИЯ
№ 715 Найти все корни уравнения, принадлежащие отрезку
[ -π/2; 3π/2] :
1) cos 2x= ½
Решение: На отрезке
[ -π/2; 3π/2] корнем уравнения cos 2x = 1/2 является число 2х=arccos (1/2) = π/3. Решая уравнение 2х = π/3, получим х = π/6Ответ : х = π/6
Слайд 38
УПРАЖНЕНИЯ
№ 715 Найти все корни уравнения, принадлежащие отрезку
[ -π/2; 3π/2] :
2) cos 3x= /2
Решение: На
отрезке [ -π/2; 3π/2] корнем уравнения cos 3x = /2 является число 3х=arccos ( /2) = π/6. Решая уравнение 3х = π/6, получим х = π/18Ответ : х = π/18
Слайд 39
УПРАЖНЕНИЯ
№ 716 Найти все решения неравенства , принадлежащие
отрезку [ -π/2; 3π/2] :
1) cos 2x< ½
Решение: На
отрезке [ -π/2; 3π/2] корнем уравнения cos 2x = 1/2 является число 2х=arccos (1/2) = π/3. Решая неравенство π/3 <2х < 3π/2, получим π/6 < х < 3π/4Ответ : π/6 < х < 3π/4
Слайд 40
УПРАЖНЕНИЯ
№ 716. Найти все корни уравнения, принадлежащие отрезку
[ -π/2; 3π/2] :
2) cos 3x> /2
Решение: На
отрезке [ -π/2; 3π/2] корнем уравнения cos 3x = /2 является число 3х=arccos ( /2) = π/6. Решая неравенство 0< 3х < π/6, получим 0< х <π/18Ответ : 0< х <π/18
Слайд 41
УПРАЖНЕНИЯ
№ 717 Построить график функции и выяснить её
свойства:
1) y=1+cos x
Решение : График функции y=cos x+1 получается
из графика функции y=cos x смещением по оси ОУ на 1 единицу.у
2 y=cos x +1
1
- π/2 0 π/2 π 3π/2
Cвойства функции: 1) ООФ – вся числовая прямая
Слайд 42
2) Область значений функции - [ 0; 2]
3) Периодическая с периодом - 2π
4) четная
5)
принимает значение, равное 0, при х= π+2 πn, nє Z Наибольшее значение , равное 2, принимает при x= 0, nє Z и в точках, получаемых сдвигом на 2 πn, nє Z
Наименьшее значение, равное 0, принимает при x= π и в точках, получаемых сдвигом на 2 πn, nє Z .
Положительные значения на интервале на всей числовой прямой, кроме точек, в которых значение функции равно 0.
Отрицательных значений у функции нет.
6)Возрастает на отрезке (π; 2π) и на отрезках, получаемых сдвигом на 2 πn, nє Z
7) Убывает на отрезке (0; π) и на отрезках, получаемых сдвигом на 2 πn, nє Z
Слайд 43
УПРАЖНЕНИЯ
№ 718 Найти множество значений функции y=cos x
, если х принадлежит промежутку :
1) [ π/3; π]
Решение : Найдем значения функции на концах промежутка. Cos (π/3) = ½; соs (π)=-1. На заданном промежутке функция строго убывающая, значит, множество значений функции – отрезок [ -1 ; ½ ]
Ответ: [ -1 ; ½ ]





























