- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Из истории логарифмов
Содержание
- 2. С точки зрения вычислительной практики, изобретение логарифмов
- 3. Потребность в сложных расчётах в XVI веке
- 4. Первый изобретатель логарифмов — шотландский барон Джон
- 5. Швейцарский математик Йост Бюрги (1552-1632), работавший в
- 6. Термин логарифм, предложенный Непером, утвердился в науке.
- 7. Иоганн КеплерК сожалению, все значения таблицы Непера
- 8. Близкое к
- 9. Что такое логарифм?Логарифм возник из сочетания греческих
- 10. ЛОГАРИФМ - число, применение которого позволяет упростить
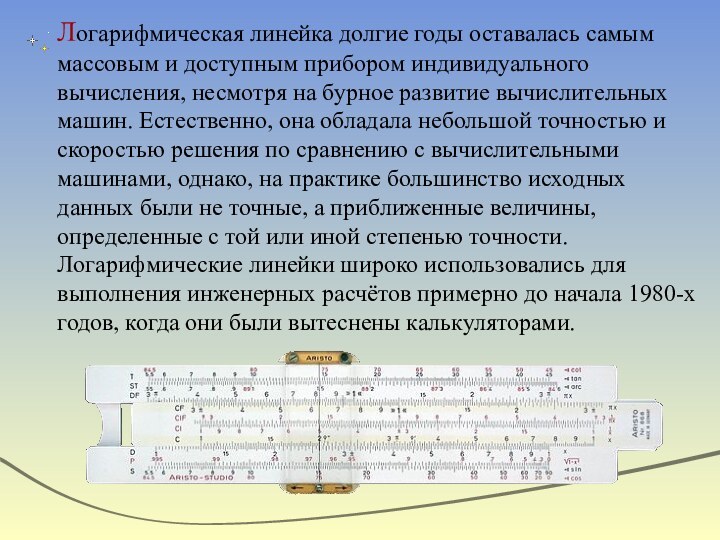
- 11. Логарифмическая линейкаПрообразом логарифмической линейки явилась так называемая
- 12. Принцип действия логарифмической линейки основан на том,
- 13. В 1654 году англичанин Роберт Биссакер разработал
- 14. В 1850 году девятнадцатилетний французский офицер Амедей
- 15. Логарифмическая линейка долгие годы оставалась самым массовым
- 16. В начале XXI века логарифмические линейки получили
- 17. Логарифмическая спиральСпираль – это плоская кривая линия,
- 18. Первым ученым, открывшим эту удивительную кривую, был
- 19. Особенности логарифмической спирали поражали не только математиков.
- 20. Логарифмическая спираль в природеРога таких рогатых млекопитающих, как архары – горные козлы, закручены по логарифмической спирали.
- 21. В подсолнухе семечки расположены по дугам близким к логарифмическим спиралям.
- 22. Один из наиболее распространенных видов пауков, Эпейра,
- 23. Хищные птицы кружат над добычей по логарифмической
- 24. По логарифмическим спиралям закручены и многие галактики, в частности, галактика, к которой принадлежит Солнечная Система.
- 25. Молекулы ДНК имеют огромную по молекулярным масштабам
- 26. Применение логарифмовТак называемые ступени темперированной хроматической гаммы
- 27. Физика — интенсивность звука (децибелы). Астрономия
- 28. «Изобретение логарифмов, сократив работу астронома, продлило ему жизнь» П.С.ЛапласПьер-Симон Лаплас
- 29. Успенский Я. В. Очерк истории логарифмов. Петроград, 1923. http://informat444.narod.ru/museum/1_17_111.htmИсточники:
- 30. Скачать презентацию
- 31. Похожие презентации





























Слайд 3 Потребность в сложных расчётах в XVI веке быстро
росла, и значительная часть трудностей была связана с умножением
и делением многозначных чисел.В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и
Михаэль Штифель
арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.
Слайд 4
Первый изобретатель логарифмов — шотландский барон Джон Непер
(1550—1617)
В 1614 году шотландский математик-любитель Джон Непер опубликовал на
латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов,
косинусов и тангенсов,
с шагом 1'.
Слайд 5 Швейцарский математик Йост Бюрги (1552-1632), работавший в Праге,
пришел к логарифмам раньше, но опубликовал свои таблицы с
опозданием (в 1620г.), после того, как в 1614г. появилась работа Непера «Описание удивительной таблицы логарифмов».Йост Бюрги
Слайд 6 Термин логарифм, предложенный Непером, утвердился в науке. Понятия
функции тогда ещё не было, и Непер определил логарифм
кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M масштабный множитель, введённый для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения).Непер взял M = 10000000.
Непер же придумал в 1617 г. другой - не логарифмический - способ перемножения чисел и разработал оригинальный прибор для быстрого умножения — палочки Непера.
палочки Непера
Слайд 7
Иоганн Кеплер
К сожалению, все значения таблицы Непера содержали
вычислительную ошибку после шестого знака. Однако это не помешало
новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялисьмногие европейские
математики,
включая Кеплера.
Слайд 8 Близкое к современному
понимание
логарифмирования как операции, обратной возведению в степень впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды,особо отметил роль
натурального логарифма.
Леонард Эйлер
Джон Валлис
Иоганн Бернулли
Слайд 9
Что такое логарифм?
Логарифм возник из сочетания греческих слов
logos - отношение, соотношение и arithmos - число.
Открытие
логарифма было связано в первую очередь с быстрым развитием астрономии в XVI в., уточнением астрономических наблюдений и усложнением астрономических выкладок.Слайд 10 ЛОГАРИФМ - число, применение которого позволяет упростить многие
сложные операции арифметики. Использование в вычислениях вместо чисел их
логарифмов позволяет заменить умножение более простой операцией сложения, деление – вычитанием, возведение в степень – умножением и извлечение корней – делением.
Слайд 11
Логарифмическая линейка
Прообразом
логарифмической
линейки явилась так
называемая гунтерова
линейка (Gunter's line), которая была изобретена английским математиком Э.
Гунтером вскоре после открытия логарифмов. Он разработал шкалу, состоящую из нескольких отрезков, располагающихся параллельно на деревянной или медной пластине. На каждый отрезок наносились деления, соответствующие логарифмам чисел или тригонометрических величин. Обычно такая шкала использовалась вместе с двумя циркулями, позволяющими быстро и точно определять длину результирующего отрезка.Слайд 12 Принцип действия логарифмической линейки основан на том, что
умножение и деление чисел заменяется соответственно сложением и вычитанием
их логарифмов.Первый вариант линейки разработал английский математик-любитель Уильям Отред в 1622 году.
Отред изготовил два типа логарифмических линеек – прямоугольную и круглую.
Уильям Отред
Слайд 13 В 1654 году англичанин Роберт Биссакер разработал прямоугольную
логарифмическую линейку, состоящую из трех частей длиной 60 см,
закрепленных параллельно друг другу. Две внешние части были неподвижно закреплены с помощью медных оправ, а третья (движок) свободно передвигалась между ними. Каждой шкале на неподвижных частях соответствовала аналогичная шкала на движке. Причем шкалы были на обеих сторонах логарифмической линейки.Слайд 14 В 1850 году девятнадцатилетний французский офицер Амедей Маннхейм
создал прямоугольную логарифмическую линейку, ставшую прообразом современных линеек и
обеспечивающую точность до трех десятичных знаков.Этот инструмент он описал в книге «Модифицированная вычислительная линейка», изданной в 1851 году.
В течение 20-30 лет эта модель выпускалась только во Франции, а затем ее стали изготавливать в Англии, Германии и США. Вскоре линейка Маннхейма завоевала популярность во всем мире.
Слайд 15 Логарифмическая линейка долгие годы оставалась самым массовым и
доступным прибором индивидуального вычисления, несмотря на бурное развитие вычислительных
машин. Естественно, она обладала небольшой точностью и скоростью решения по сравнению с вычислительными машинами, однако, на практике большинство исходных данных были не точные, а приближенные величины, определенные с той или иной степенью точности. Логарифмические линейки широко использовались для выполнения инженерных расчётов примерно до начала 1980-х годов, когда они были вытеснены калькуляторами.Слайд 16 В начале XXI века логарифмические линейки получили второе
рождение в наручных часах: следуя моде, производители некоторых марок
(среди которых Breitling, Citizen, Orient) выпустили модели со встроенной логарифмической линейкой, выполненной в виде вращающихся колец со шкалами вокруг циферблата.Производители обычно называют такие устройства «навигационная линейка». Их достоинство — можно сразу, в отличие от микрокалькулятора, получить информацию, соответствующую табличной форме представления (например, таблицу расхода топлива на пройденное расстояние, перевода миль в километры и тому подобное).
Слайд 17
Логарифмическая спираль
Спираль – это плоская кривая линия, многократно
обходящая одну из точек на плоскости, называемую полюсом спирали.
Логарифмическая спираль является траекторией точки, которая движется вдоль равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному
расстоянию. Точнее, в логарифмической спирали углу поворота пропорционален логарифм этого расстояния.
Слайд 18 Первым ученым, открывшим эту удивительную кривую, был Рене
Декарт (1596-1650г.г.).
В математике логарифмическая спираль впервые упоминается в
1638 году. Рене Декарт
Слайд 19
Особенности логарифмической спирали
поражали не только математиков. Ее
свойства
удивляют и биологов, которые считают именно
эту спираль
своего рода стандартом биологических объектов самой разной природы.
Например, раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее аналогиям.
Поэтому раковины многих моллюсков, улиток, закручены по логарифмической спирали.
Слайд 20
Логарифмическая спираль в природе
Рога таких рогатых млекопитающих, как
архары – горные козлы, закручены по логарифмической спирали.
Слайд 22 Один из наиболее распространенных видов пауков, Эпейра, сплетая
паутину, закручивает нити вокруг центра по логарифмической спирали.
Слайд 23 Хищные птицы кружат над добычей по логарифмической спирали.
Дело в том, что они лучше видят, если смотрят
не прямо на добычу, а чуть в сторону.Слайд 24 По логарифмическим спиралям закручены и многие галактики, в
частности, галактика, к которой принадлежит Солнечная Система.
Слайд 25 Молекулы ДНК имеют огромную по молекулярным масштабам длину
и состоят из 2-х нитей, сплетённых между собой в
двойную спираль.Каждую из нитей можно сравнить с длинной ниткой бус.
Слайд 26
Применение логарифмов
Так называемые ступени темперированной хроматической гаммы (12-
звуковой) частот звуковых колебаний представляют собой логарифмы.
Только основание
этих логарифмов равно 2 (а не 10, как принято в других случаях). Номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков.
Слайд 27
Физика — интенсивность звука (децибелы).
Астрономия —
шкала яркости звёзд.
Химия — активность водородных ионов (pH).
Сейсмология — шкала Рихтера.Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
История — логарифмическая шкала времени.
Логарифмическая функция крайне важна в экономике, физике, при проведении научных, экспериментальных расчетов, астрономии и др.
Форма логарифмической спирали присуща многим природным объектам.