многогранника и призмы; элементов многогранника
и призмыб) узнать виды призм;
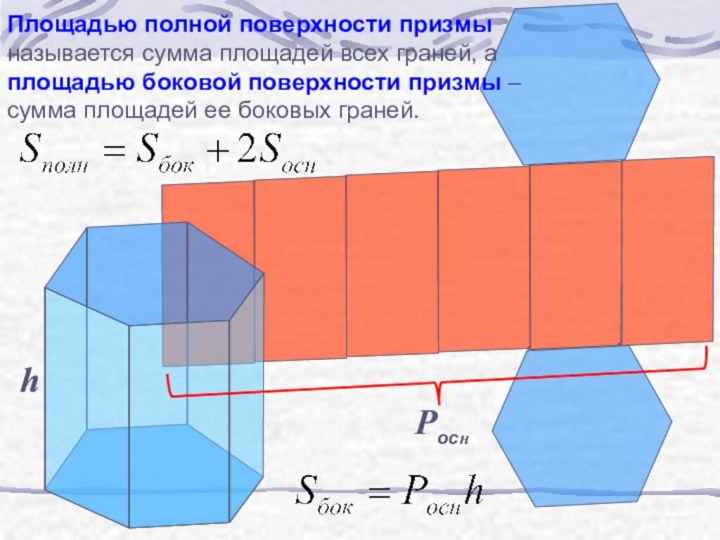
в) вывести формулы для вычисления площадей
полной и боковой поверхностей призмы
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку геометрии на тему Многогранник.Призма.
Содержание
- 2. Тема урока: ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМАЦели урока:а) построить
- 4. ПРОСТРАНСТВОмногогранникивыпуклыеневыпуклыеПоверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.
- 5. Прямоугольный параллелепипедМногогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
- 6. Невыпуклый многогранник
- 7. Параллелепипед – поверхность, составленная из шести параллелограммов.
- 8. Тетраэдр – поверхность, составленная из четырех треугольников.
- 9. Октаэдр составлен из восьми треугольников.Многоугольники, из которых
- 10. ПризмаА1А2АnB1B2BnB3А3Многогранник, составленный из двух равных многоугольников А1А2…Аn
- 11. ПризмаА1А2АnB1B2BnB3А3Отрезки А1В1, А2В2 и т.д. - боковые
- 12. Если боковые ребра перпендикулярны к основаниям, то
- 13. Прямая призма называется правильной, если ее основания
- 14. Площадью полной поверхности призмы называется сумма площадей
- 17. ЕГЭ. Задачи В 9.1. Основание прямой призмы
- 18. АВСС1В1А12D
- 19. Что нового вы узнали на уроке?2. Что
- 20. Скачать презентацию
- 21. Похожие презентации
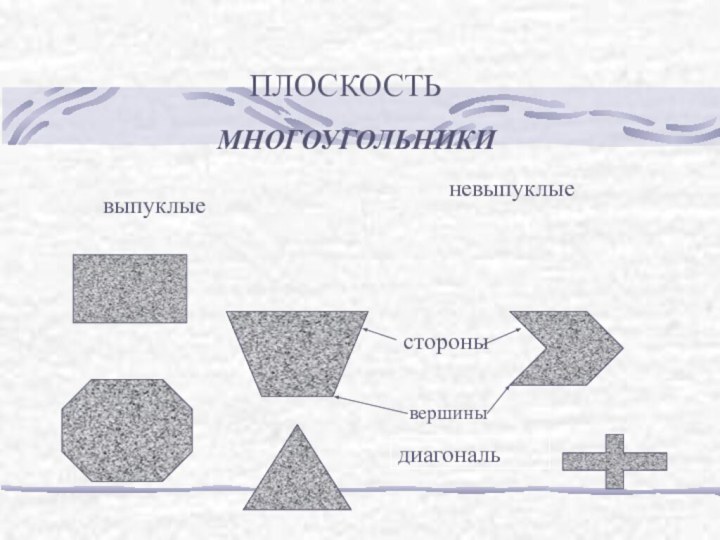
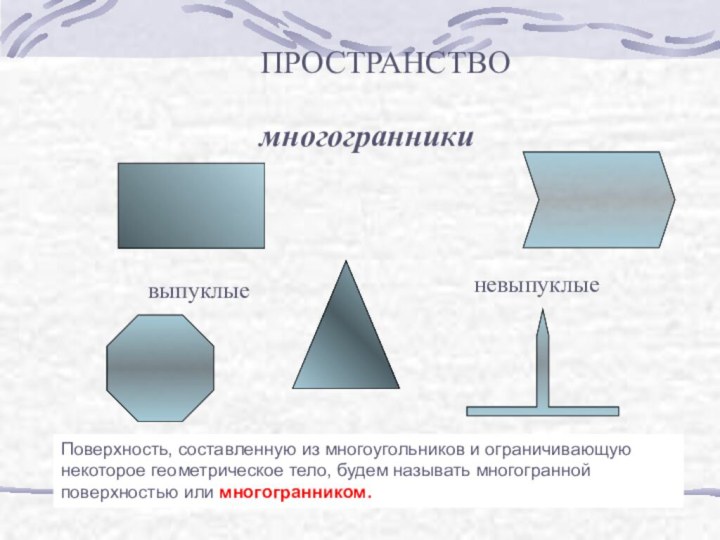
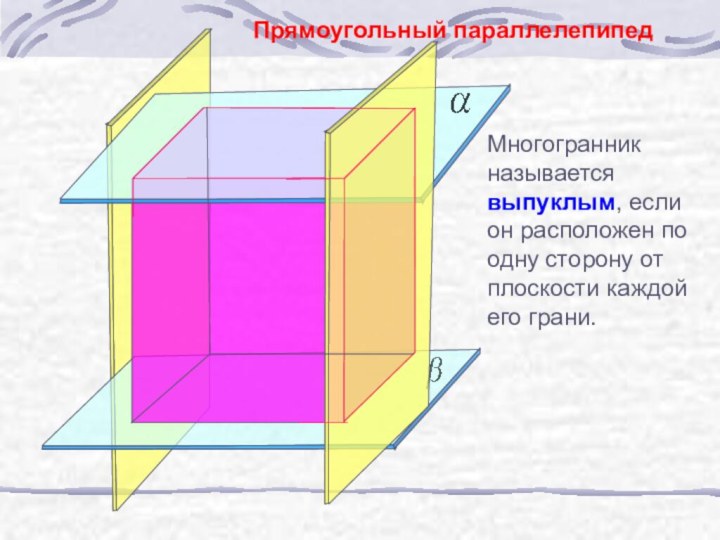
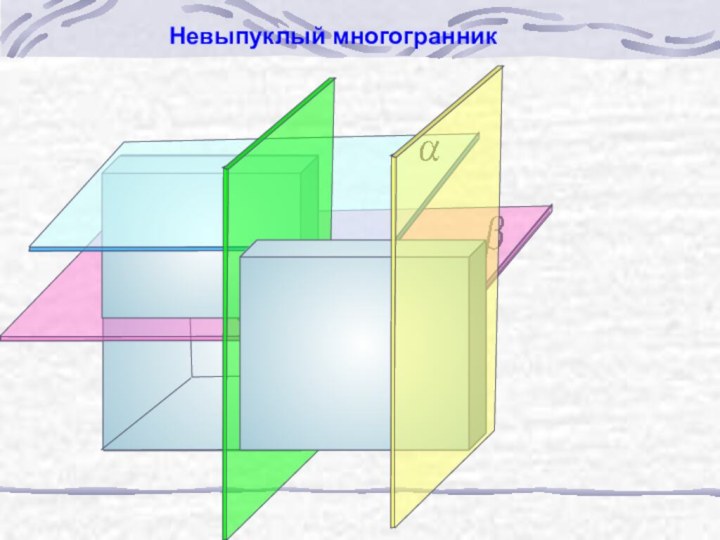
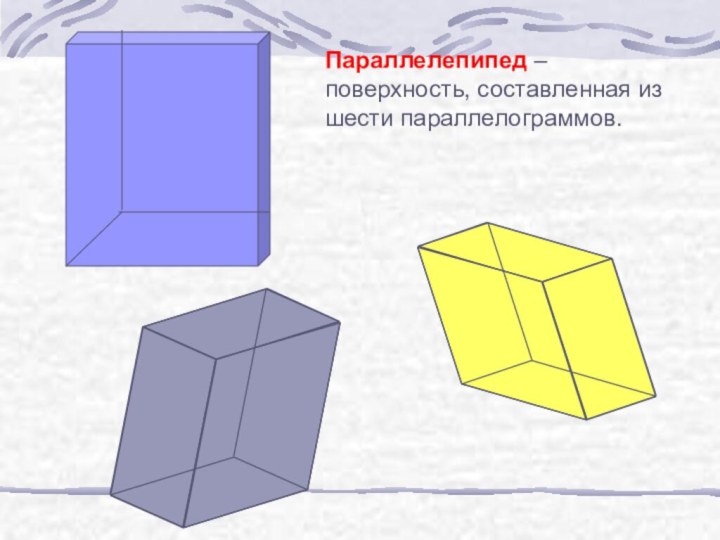
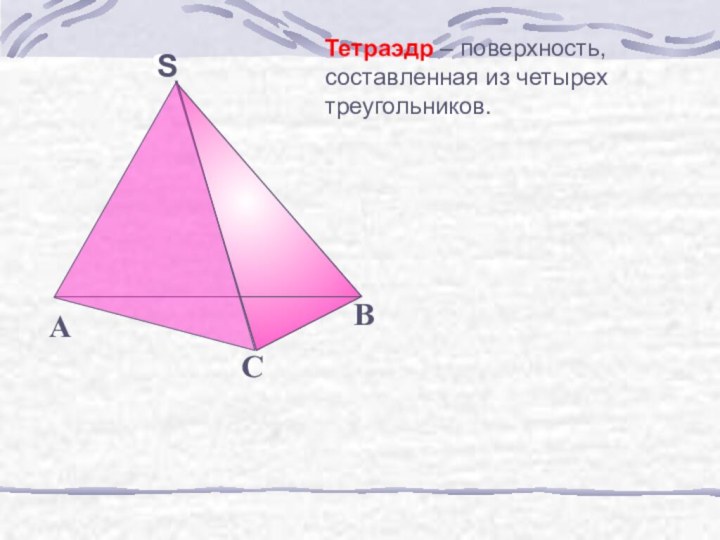
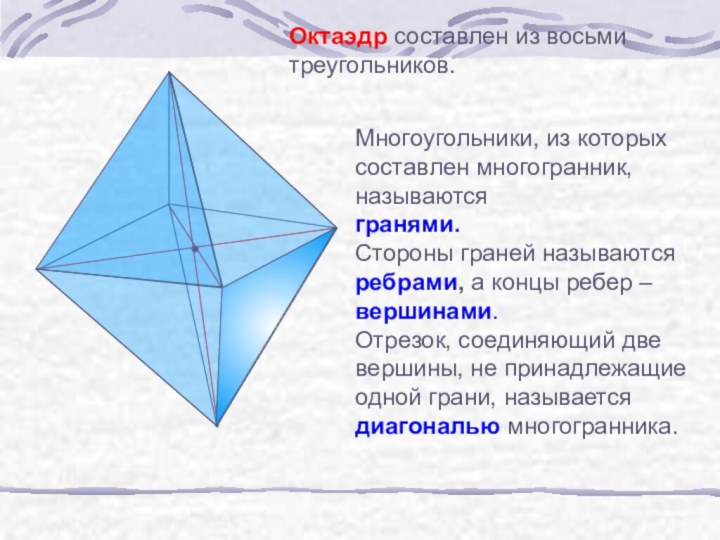
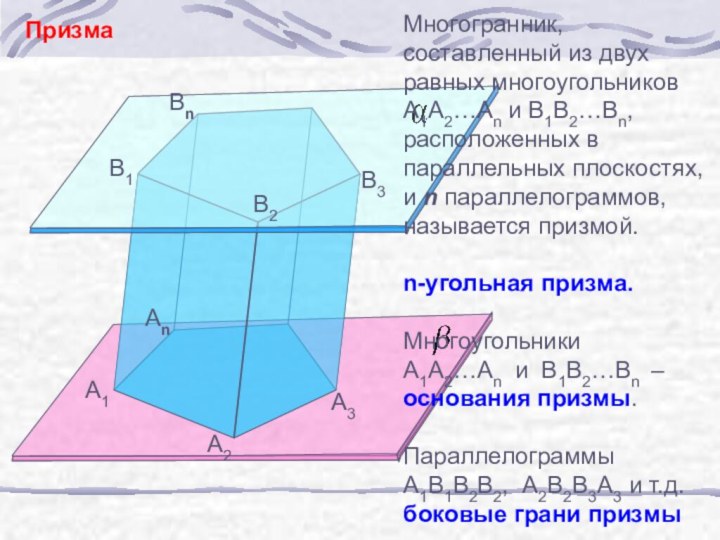
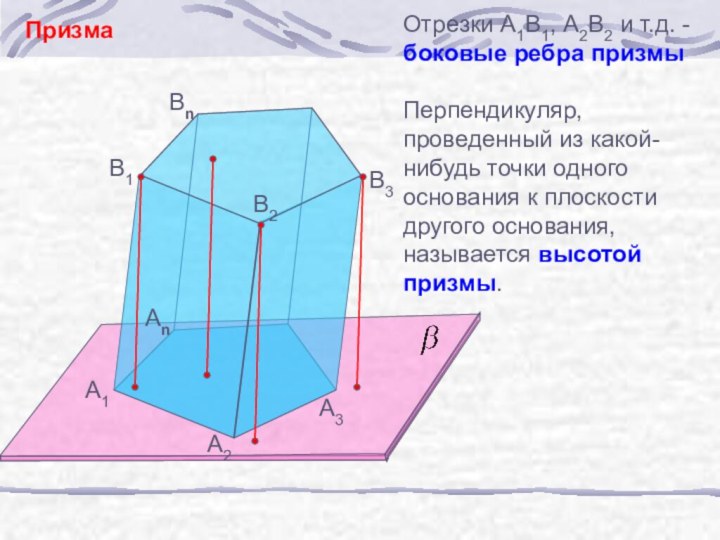
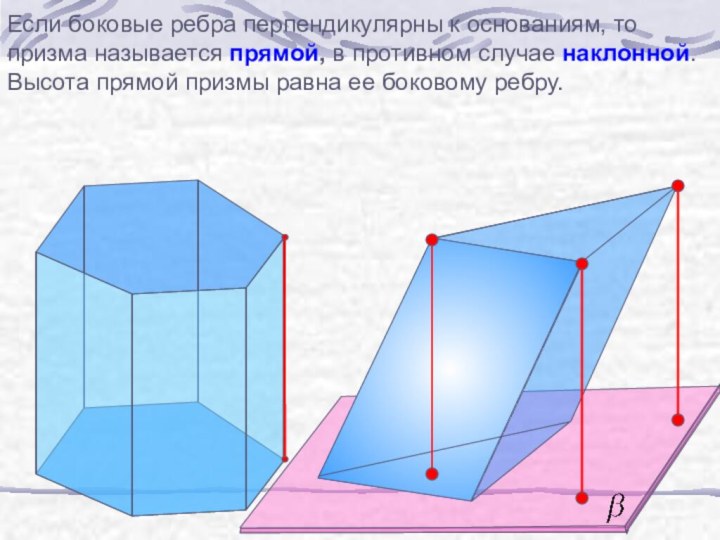
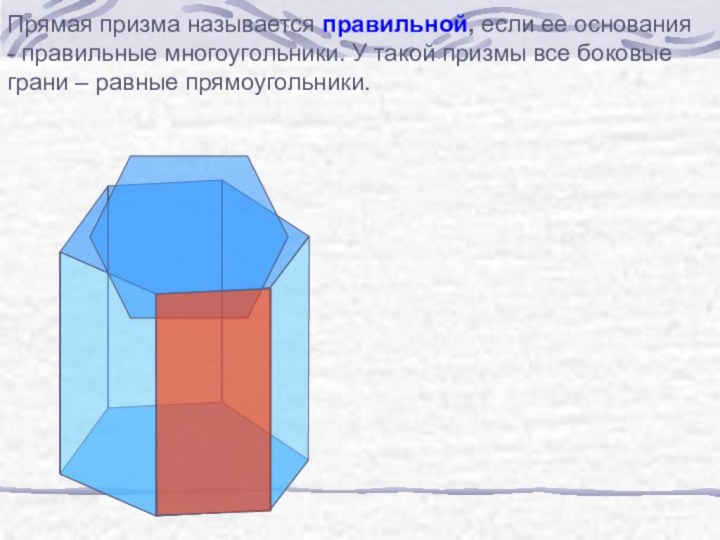
Тема урока: ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМАЦели урока:а) построить определение: многогранника и призмы; элементов многогранника и призмыб) узнать виды призм; в) вывести формулы для вычисления площадей полной и боковой поверхностей призмы
Слайд 2
Тема урока:
ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА
Цели урока:
а) построить определение:
Слайд 4
ПРОСТРАНСТВО
многогранники
выпуклые
невыпуклые
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое
тело, будем называть многогранной поверхностью или многогранником.
Слайд 5
Прямоугольный параллелепипед
Многогранник называется выпуклым, если он расположен по
одну сторону от плоскости каждой его грани.
Слайд 9
Октаэдр составлен из восьми треугольников.
Многоугольники, из которых составлен
многогранник, называются
гранями.
Стороны граней называются ребрами, а концы ребер
– вершинами.Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Слайд 10
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Многогранник, составленный из двух равных многоугольников А1А2…Аn и
В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется
призмой.n-угольная призма.
Многоугольники
А1А2…Аn и В1В2…Вn – основания призмы.
Параллелограммы А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы
Слайд 11
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Отрезки А1В1, А2В2 и т.д. -
боковые ребра
призмы
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости
другого основания, называется высотой призмы.
Слайд 12
Если боковые ребра перпендикулярны к основаниям, то призма
называется прямой, в противном случае наклонной.
Высота прямой призмы равна
ее боковому ребру.
Слайд 13
Прямая призма называется правильной, если ее основания -
правильные многоугольники. У такой призмы все боковые грани –
равные прямоугольники.
Слайд 14 Площадью полной поверхности призмы называется сумма площадей всех
граней, а площадью боковой поверхности призмы – сумма площадей
ее боковых граней.h
h
Pocн
Слайд 15
В прямоугольном параллелепипеде стороны основания равны 12 см
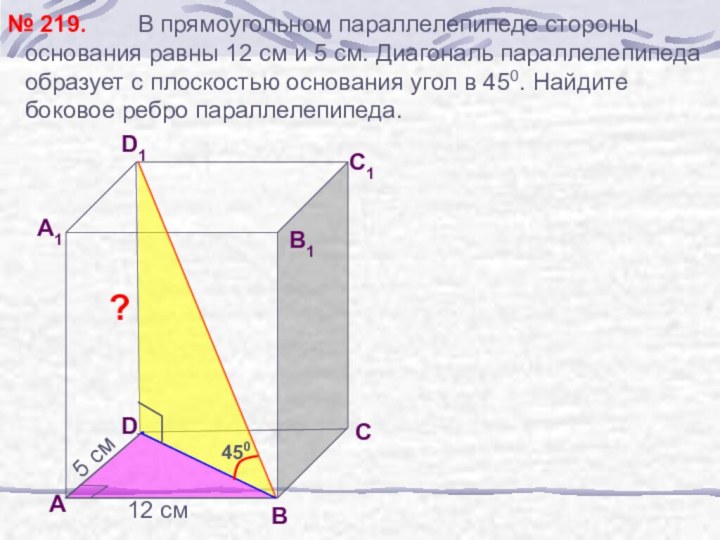
и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.№ 219.
В
С
А1
D1
С1
В1
?
D
А
12 см
5 см
Слайд 16
Основанием прямого параллелепипеда является ромб с диагоналями 10
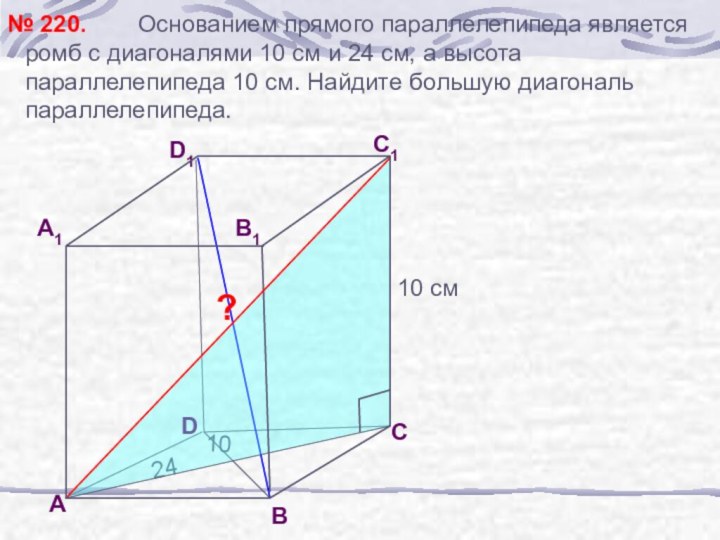
см и 24 см, а высота параллелепипеда 10 см. Найдите большую диагональ параллелепипеда.№ 220.
В
С
А1
D1
С1
В1
?
D
А
24
10
10 см
Слайд 17
ЕГЭ. Задачи В 9.
1. Основание прямой призмы –
прямоугольный треугольник с катетами 6 и 8. Высота призмы
равна10. Найдите площадь боковой и полной поверхности призмы.2. Найдите площадь полной поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными
3 и 4, и боковым ребром, равным 5.
3. Найдите боковое ребро правильной четырёхугольной призмы, если стороны её основания равны 3, а площадь поверхности равна 66.
Слайд 19
Что нового вы узнали на уроке?
2. Что использовали
