- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Аксиомы геометрии
Содержание
- 2. Евклид и его труды III в до н.э.
- 3. Такой подход, когда сначала формируются исходные положения-аксиомы,
- 4. Николай Иванович Лобачевский начало XIX в.
- 5. С современной точки зрения можно дать,
- 6. на эллиптической плоскости "точка" представлена двумя точками-антиподами
- 7. ЛЮБАЯ ПОЛУПРЯМАЯ, например t, являющаяся
- 8. ПАРАЛЛЕЛЬНЫЕ BC и BD к r, проходящие
- 9. АКСИОМА 1 Через любые две точки проходит прямая и притом только одна
- 10. АКСИОМА 2 На любом луче от его
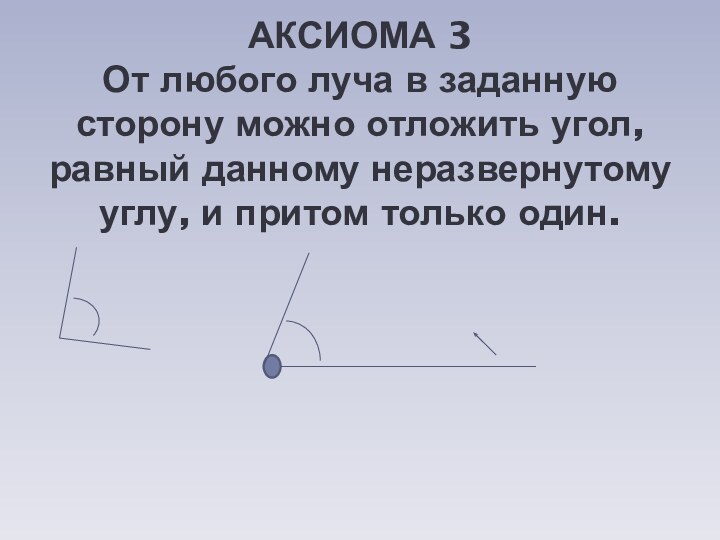
- 11. АКСИОМА 3 От любого луча в заданную
- 12. Аксиома 4 Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
- 13. Следствие 1Если прямая пересекает одну из двух
- 14. Скачать презентацию
- 15. Похожие презентации
Евклид и его труды III в до н.э.









Слайд 5 С современной точки зрения можно дать, например,
следующее определение Л. г. на плоскости: она есть не
что иное, как геометрия внутри круга на обычной (евклидовой) плоскости, лишь выраженная особым образом. Именно, рассматривают круг на обычной плоскости (рис. 1) и внутренность его, т. е. круг, за исключением ограничивающей его окружности, называют «плоскостью».Лобачевский ,как бы рассматривает геометрию сразу в масштабе нашей планеты.
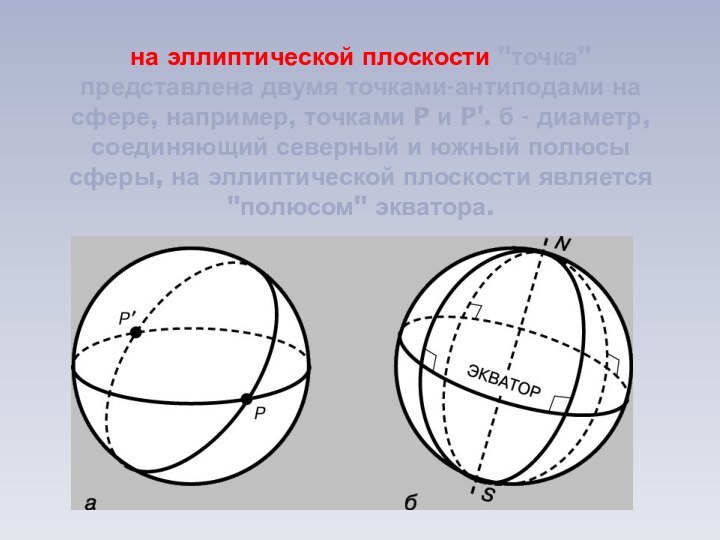
Слайд 6 на эллиптической плоскости "точка" представлена двумя точками-антиподами на
сфере, например, точками P и P'. б - диаметр,
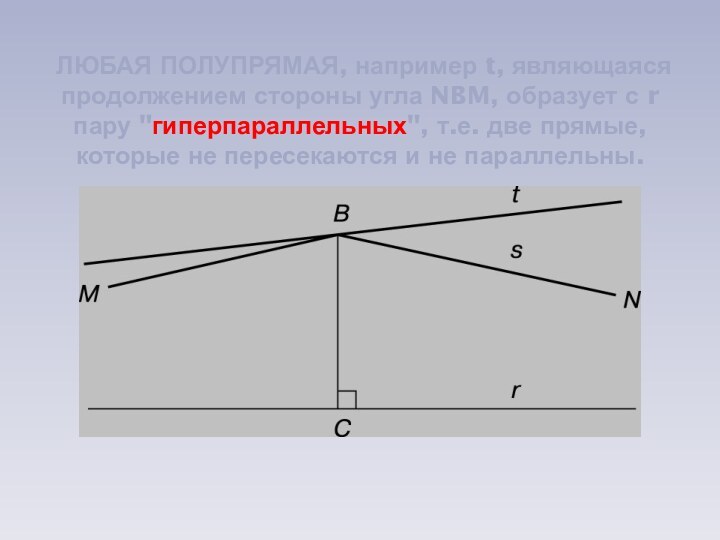
соединяющий северный и южный полюсы сферы, на эллиптической плоскости является "полюсом" экватора.Слайд 7 ЛЮБАЯ ПОЛУПРЯМАЯ, например t, являющаяся продолжением стороны
угла NBM, образует с r пару "гиперпараллельных", т.е. две
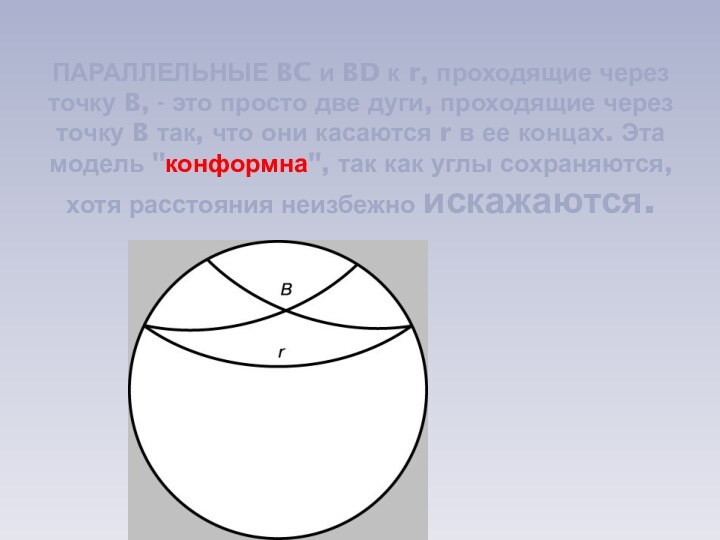
прямые, которые не пересекаются и не параллельны.Слайд 8 ПАРАЛЛЕЛЬНЫЕ BC и BD к r, проходящие через
точку B, - это просто две дуги, проходящие через
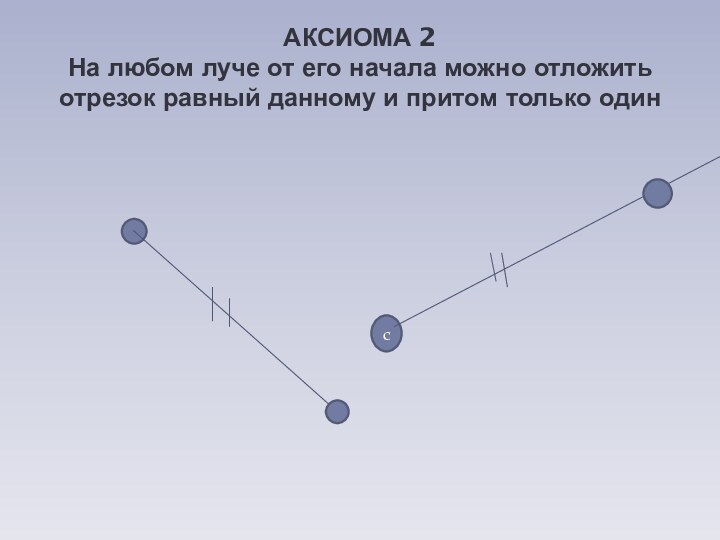
точку B так, что они касаются r в ее концах. Эта модель "конформна", так как углы сохраняются, хотя расстояния неизбежно искажаются.Слайд 10 АКСИОМА 2 На любом луче от его начала можно
отложить отрезок равный данному и притом только один
с
Слайд 11 АКСИОМА 3 От любого луча в заданную сторону можно
отложить угол, равный данному неразвернутому углу, и притом только
один.
Слайд 12 Аксиома 4 Через точку, не лежащую на данной прямой,
проходит только одна прямая, параллельная данной.
Слайд 13
Следствие 1
Если прямая пересекает одну из двух параллельных
прямых, то она пересекает и другую.
c a
b





























