как длину отрезка AB , если отрезок AB удается
включить в некоторый треугольник в качестве одной из его сторон;2) по формуле
3) по формуле
1.1. Расстояние между двумя точками
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








1.1. Расстояние между двумя точками
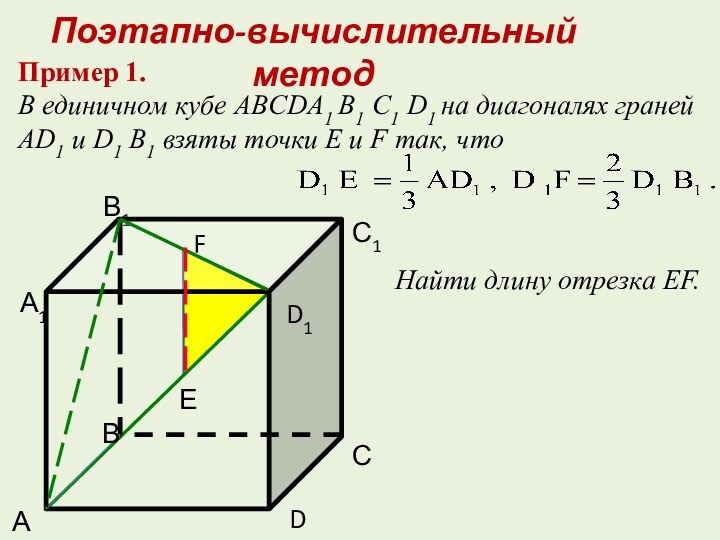
Найти длину отрезка EF.
Поэтапно-вычислительный метод
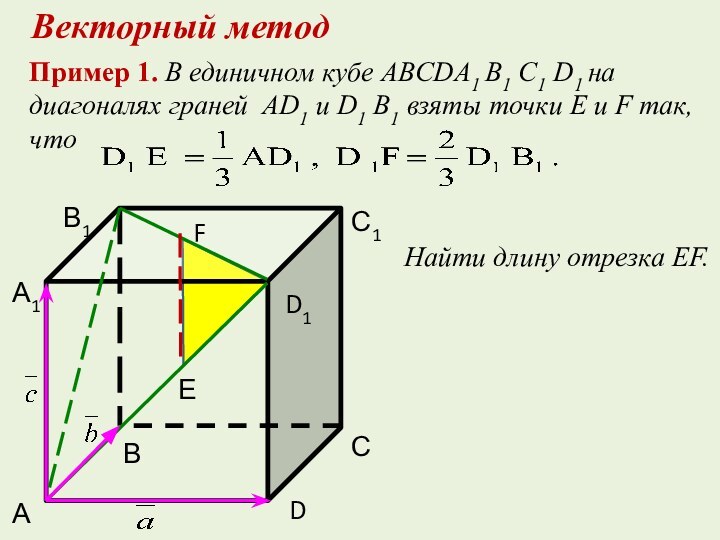
Найти длину отрезка EF.
Векторный метод
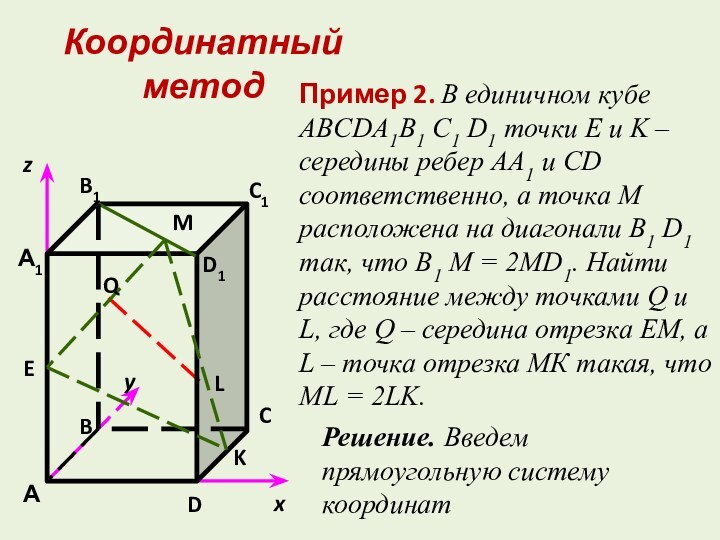
Координатный метод