Презентация на тему Арифметическая прогрессия в древности

II тыс. до н.э., содержат примеры задач на арифметическую

прогрессию. Каких-либо теоретических сведений о прогрессии в них не приводится , а даются лишь указания ,какие действия надо выполнять для получения ответа на вопрос задачи. Вот пример задачи из египетского папируса АХМЕСА : «Пусть тебе сказано : раздели 10 мер ячменя между 10 человеками , разность же между каждым человеком и его соседом равна 1/8 меры.» Попытайтесь его решить дома .

себе изобретателя шахматной игры , своего подданного СЕТУ ,

чтобы наградить его за остроумную выдумку . СЕТА , издеваясь над царем , потребовал за первую клетку шахматной доски 1 зерно , за вторую- 2зерна , за третью- 4 зерна и т.д. Обрадованный царь приказал выдать такую ,,скромную,, награду. Однако оказалось , что царь не в состоянии выполнить желание СЕТЫ , так как нужно было выдать количество зерен равное сумме геометрической прогрессии
1,2,
ЕЕ сумма равна
Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности ЗЕМЛИ.

Геометрическая прогрессия в древности. ЗАДАЧА-ЛЕГЕНДА

правила , которые можно рассматривать как формулы сумм первых

n членов прогрессий. Архимеду была известна и формула суммы бесконечной геометрической прогрессии, которую он использовал для вычисления площадей фигур и объемов тел, применяя им открытый метод « исчерпывания «.
Для решения задач геометрии и механики Архимед вывел формулу суммы квадратов первых n натуральных чисел:

Прогрессии древней Греции

АРХИМЕД

ЕВКЛИД

математик, астроном и физик. Родился 30 апреля 1777 в

Брауншвейге. Необыкновенные способности к математике и иностранным языкам проявились у Карла еще в детстве. Восьмилетний мальчик поразил учителя, сосчитав необычным образом сумму целых чисел от 1 до 100: он сообразил, что сумма пар чисел, равноудаленных от концов, одинакова: 1 + 100 = 2 + 99 = 3 + 98 =... = 50 + 51 = 101, и что таких пар ровно 50, поэтому искомая сумма равна 101ґ50 = 5050. Сам того не подозревая, Гаусс переоткрыл формулу для определения суммы членов арифметической прогрессии.

РОЛЬ К. ГАУССА

рассмотренных примерах применялись две различные
Схемы начисления процентов : в

1 задаче речь идет о простых процентах , в 2 задаче
Речь идет о сложных процентах.

В самых различных жизненных ситуациях очень часто приходится выполнять денежные расчеты. Рассмотрим два примера .ЗАДАЧА 1.
Ежемесячно каждая семья платит за электроэнергию в среднем 2000 сум. За каждый просроченный день взимается пеня в размере 0,5% с оплачиваемой суммы.
Сколько заплатит семья за электроэнергию, если они просрочат оплату на 1день; на n-дней?
Решение: так как 0,5% от 2000сум составляют 10 сум., то за каждый просроченный день сумма штрафа будет увеличиваться на 10 сум, и придется заплатить 2000+10=2010 сум.

ЗАДАЧА 2.
Вы , вероятно , знаете , что за хранение денег в банке вкладчику начисляют проценты. Пусть на счет в банке , который выплачивает 20% годовых , положили 1000$ и оставили эти деньги на счете на год.
Какой будет новая сумма вклада через год , через n лет?
РЕШЕНИЕ: Через год начальная сумма вклада увеличится на 20% , значит новая сумма составит от первоначальной 120%.Таким образом , через год вклад увеличится в 120/100=1,2 раза и составит 1000*1,2=1200$. Еще через год снова увеличится в 1,2 раза. Следовательно ,через 2 года на счете будет
1200*1,2=1440$

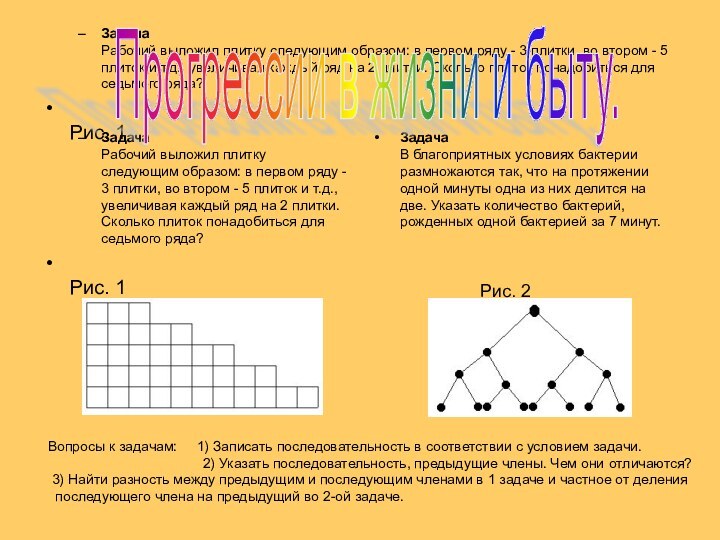
Прогрессии в жизни и быту

Вы , наверное , заметили , что в рассмотренных примерах применялись две различные
Схемы начисления процентов : в 1 задаче речь идет о простых процентах , в 2 задаче
Речь идет о сложных процентах.