- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему научно-исследовательского проекта Математические функции в нашей жизни
Содержание
- 2. Проект выполнил: Мурашев Александр Студент группы № 224-МЭПОРуководитель проекта: Преснякова Оксана Владимировна Преподаватель математики, ВКК
- 3. В курсе математики средней и старшей школы
- 4. Зависимости между величинами.Уходит корнями в ту далекую
- 5. Исследования общих зависимостей.Исследования общих зависимостей началось в
- 6. Понятие переменной величины.Это понятие было введено в
- 7. Общее понятие
- 8. Развитие понятия функции.Один из самых замечательных математиков
- 9. Функция - одно из основных математических и
- 10. М а т е м а
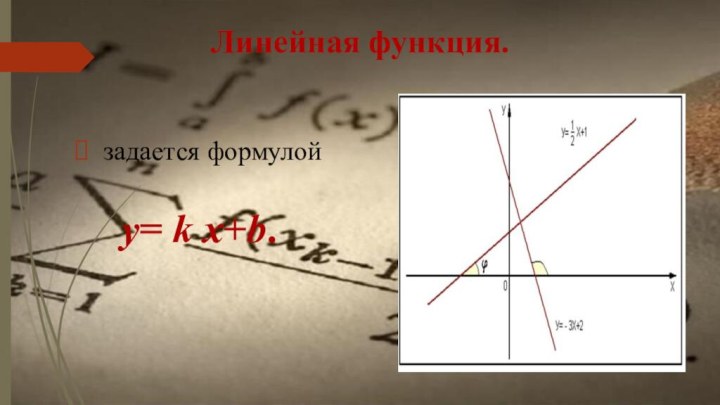
- 11. Линейная функция. задается формулой y= k x+b.
- 12. Примеры: Свеча длиной 25 см при горении
- 13. 4. Автомобиль, выехавший из пункта А, в
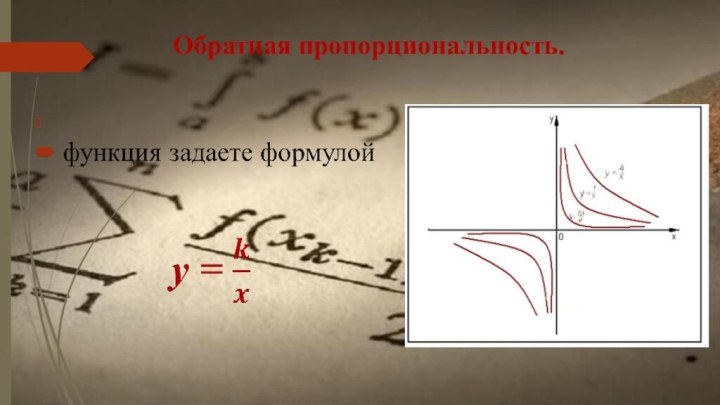
- 15. Обратная пропорциональность.
- 16. Примеры:
- 17. По данной задаче проведём практическое исследование.Исследуем зависимость
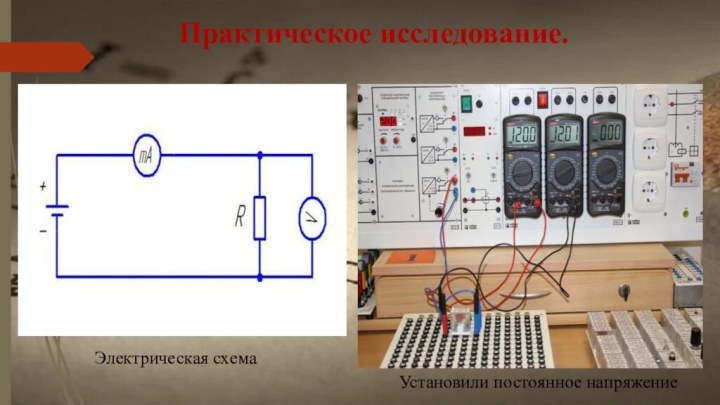
- 18. Практическое исследование. Электрическая схема Установили постоянное напряжение
- 19. Включение №1 Включение №2 Включение №3 Включение №4
- 20. По полученным данным можно построить график зависимости силы тока в цепи от сопротивления.
- 22. Квадратичная функция.
- 23. Примеры:1. Траектории некоторых космических тел (комет, астероидов и
- 24. Также параболические зеркала используются в любительских переносных
- 25. 2. При вращении сосуда с жидкостью вокруг вертикальной оси
- 26. 5. Движение баскетбольного мяча происходит по параболе.
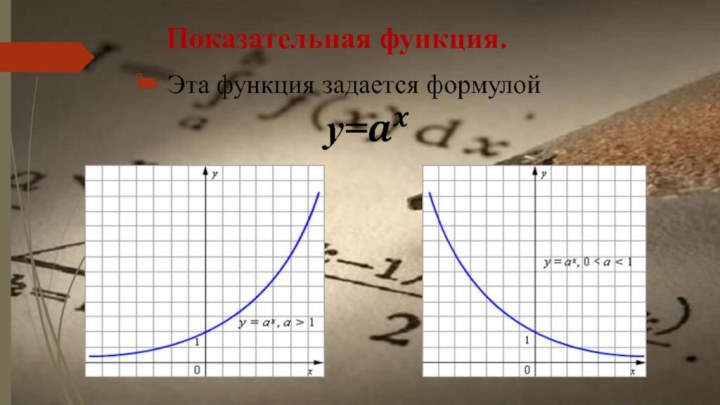
- 27. Показательная функция.
- 28. Примеры:
- 29. 2. В Сберегательном банке России для некоторых
- 30. Пусть банк начисляет p% годовых, внесенная сумма равна S р., а сумма, которая будет на счёте через n лет, равна Sn.
- 32. Тригонометрические функции.
- 33. Примеры:1. В настоящее время в интернете в
- 35. 2. Движение рыб в воде происходит по
- 36. Вывод:Проанализировав соответствующую литературу, рассмотрев применение математических функций
- 37. Скачать презентацию
- 38. Похожие презентации
Проект выполнил: Мурашев Александр Студент группы № 224-МЭПОРуководитель проекта: Преснякова Оксана Владимировна Преподаватель математики, ВКК































Слайд 3 В курсе математики средней и старшей школы мы
получаем большой объём математических знаний. Порой многие понятия курса алгебры
и математического анализа 10-11 классов носят абстрактный характер, и мы задаёмся вопросом: «А где применяются те знания, которые мы получаем на уроках математики?»Так возникла идея: исследовать в каких областях науки, техники и нашей жизни нашли применение функции. Задавшись целью, мною была проведена исследовательская работа.
Были поставлены следующие задачи:
Изучить историю развития понятия «функция»;
Найти примеры применения функций в нашей жизни и проверить в процессе практического исследования;
Оформить результаты исследования и сделать выводы.
Слайд 4
Зависимости между величинами.
Уходит корнями в ту далекую эпоху,
когда люди впервые поняли, что окружающие их явления взаимосвязаны.
Они еще не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода; чем сильнее натянута тетива лука, тем дальше полетит стрела; чем дольше горит костер, тем теплее будет в пещере.
Слайд 5
Исследования общих зависимостей.
Исследования общих зависимостей началось в XIV
веке. Среди схоластов возникла школа, утверждавшая, что качества могут
быть более или менее интенсивными (платье человека, свалившегося в воду, мокрее, чем у того, кто лишь попал под дождь). Французский ученый Николай Оресм стал изображать интенсивности длинами отрезков. Важным достижением Оресма была попытка классифицировать получившиеся графики. Он выделил три типа качеств: равномерные (то есть с постоянной интенсивностью), равномерно-неравномерные (для которых скорость изменения интенсивности постоянна) и неравномерно-неравномерные (все остальные), а также указал характерные свойства этих графиков.
Слайд 6
Понятие переменной величины.
Это понятие было введено в науку
французским философом и математиком Рене Декартом (1596-1650 гг.). Декарту
удалось уничтожить пропасть, существовавшую со времен древнегреческой математики, между геометрией и арифметикой. При записи зависимостей между величинами Декарт стал применять буквы. Отношения между известными и неизвестными величинами Декарт выражал в виде уравнений. Чтобы наглядно изображать уравнение, он заменял все величины длинами отрезков. По сути дела, здесь была заложена идея метода координат.
Слайд 7
Общее понятие функции.
Развитие
механики и техники потребовало введения общего понятия функции, что
было сделано немецким философом и математиком Г.Лейбницем. Он употреблял его в очень узком смысле, связывая только с геометрическими образами.
Слайд 8
Развитие понятия функции.
Один из самых замечательных математиков XVIII
в. - Леонард Эйлер (1707-1783 гг.), - вводя в
своем учебнике понятие функции, говорил лишь, что «когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых».Слайд 9 Функция - одно из основных математических и общенаучных
понятий, выражающее зависимость между переменными величинами. Каждая область знаний;
физика, химия, биология, социология, лингвистика и т. д. - имеет свои объекты изучения, устанавливает свойства и взаимосвязи этих объектов.
Слайд 12
Примеры:
Свеча длиной 25 см при горении уменьшается на
1,5 см за каждый час. Нетрудно сообразить, что ее
длина l через t часов будет составлять l = 25 - 1,5t .Отправляя телеграмму, мы платим по 3 р. за каждое слово и 10 р. дополнительно. Общая стоимость телеграммы выражается линейной функцией e = 3 x + 10.
Из геометрии известна теорема: «Сумма углов выпуклого многоугольника равна 180°(n - 2 )». Раскроем скобки и, обозначив искомую сумму буквой S, получим линейную функцию S = 180°n — 360°.
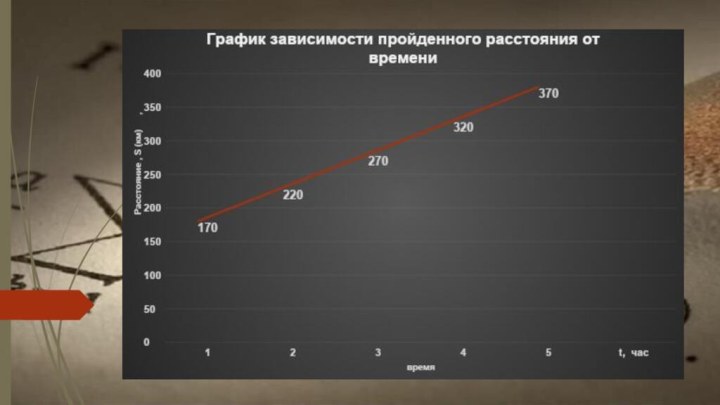
Слайд 13 4. Автомобиль, выехавший из пункта А, в настоящее
время находится от него в 120 км. На каком
расстоянии s от А будет находиться автомобиль через t ч, если он будет двигаться в том же направлении со скоростью 50 км/ч? Ответ будет выражаться линейной функцией вида s = 50 t + 120 .
Слайд 17
По данной задаче проведём практическое исследование.
Исследуем зависимость силы
тока от сопротивления.
Возьмём следующие параметры:
- напряжение U –
const;
- сопротивление R – изменяется от 100 до 470 Ом;
Соберём электрическую схему, снимем показания и произведём расчёт.
Слайд 23
Примеры:
1. Траектории некоторых космических тел (комет, астероидов и других),
проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости имеют форму параболы
(или гиперболы). Эти тела вследствие своей большой скорости не захватываются гравитационным полем звезды и продолжают свободный полёт. Для создания невесомости в земных условиях проводятся полёты самолётов по параболической траектории, так называемой параболе Кеплера. При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.Слайд 24 Также параболические зеркала используются в любительских переносных телескопах
систем Кассергена, Ньютона, Шмидта — Кассергена, а в фокусе параболы устанавливают
вспомогательные зеркала, подающие изображение на окуляр.Слайд 25 2. При вращении сосуда с жидкостью вокруг вертикальной оси поверхность
жидкости в сосуде и вертикальная плоскость пересекаются по параболе.
3.
Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.4. Форма параболы иногда используется в архитектуре для строительства крыш и куполов
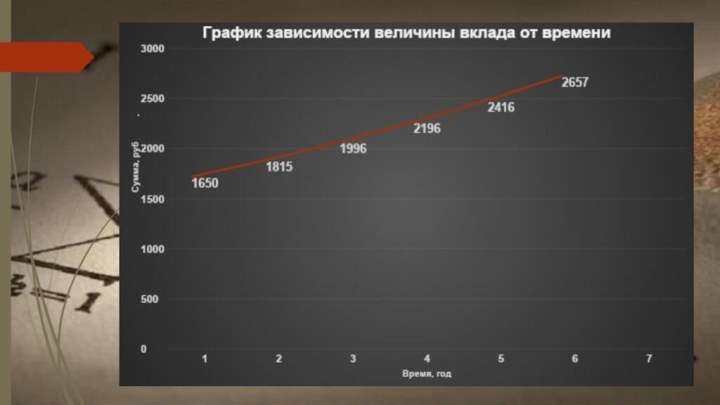
Слайд 29 2. В Сберегательном банке России для некоторых видов
вкладов (так называемых срочных вкладов, которые нельзя взять ранее, чем через
год) принята следующая система начисления денег на сумму, внесённую в банк. За первый год нахождения внесённой суммы на счёте она возрастает на некоторое число процентов, в зависимости от вида вклада. В конце года вкладчик может снять со счёта эти деньги - “проценты”, как их обычно называют. Если же он этого не сделал, то они капитализируются, т. е. присоединяются к начальному вкладу, и поэтому в конце следующего года проценты начисляются банком уже на новую, увеличенную сумму. Коротко говорят, что при такой системе начисляются “проценты на проценты”.В математике в такой ситуации обычно говорят о сложных процентах.
Подсчитаем, сколько денег получит вкладчик, скажем, через 5 лет, если он положил на счёт в банк 1500 р. И ни разу не будет брать деньги со счёта, а тем временем сумма будет ежегодно увеличиваться на 10%:
Слайд 30 Пусть банк начисляет p% годовых, внесенная сумма равна S р., а сумма,
которая будет на счёте через n лет, равна Sn.
Слайд 33
Примеры:
1. В настоящее время в интернете в открытом
доступе есть масса бесплатных программ, которые позволяют определить биоритмы
человека по дате рождения. Этот вид биоритмов человека позволяет определить те дни, в которые человек наиболее бодр и активен и те, в которые он будет обессилен и нуждаться в покое. При помощи подобных программ даже не обязательно понимать, как посчитать биоритмы человека: вы просто вводите запрашиваемые данные, а система сама выдает вам готовый график с комментариями и пояснениями.Слайд 35 2. Движение рыб в воде происходит по закону
синуса или косинуса, если зафиксировать точку на хвосте, а
потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Слайд 36
Вывод:
Проанализировав соответствующую литературу, рассмотрев применение математических функций и
проведя практическое исследование, я убедился, что математические функции являются
неотъемлемой частью нашей жизни.Все динамические процессы, такие как: работа ядерных реакторов, бег океанской волны и закономерности развития циклона, экономичное управление производством, распределение ресурсов, организация технологических процессов, прогнозирование течения химических реакций или изменения численности различных взаимосвязанных в природе видов животных и растений – всё описывают математические функции.