Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

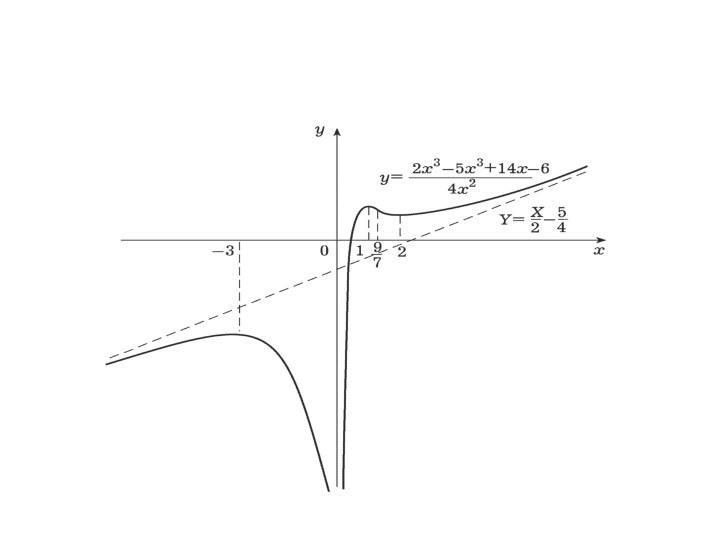
Презентация на тему Асимптоты графика функции

Содержание

2. Горизонтальные асимптоты
Лекция 15. Асимптоты графика функции 2. Горизонтальные асимптоты 3. Наклонные асимптоты ТЕОРЕМА 38. Для того чтобы график функции у=f(x) имел при х→+∞ наклонную Для дробно рациональной функции:Асимптоты на +∞ и − ∞ одновременно существуют или ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИЭлементарное исследование- область определения, непрерывность, точки разрыва, их тип 2. Промежутки возрастания, убывания, точки экстремума.3. Промежутки выпуклости, вогнутости, точки перегиба.Пример.
Слайды презентации

Слайд 2 2. Горизонтальные асимптоты

2. Горизонтальные асимптоты

Слайд 3 3. Наклонные асимптоты

3. Наклонные асимптоты

Слайд 4 ТЕОРЕМА 38. Для того чтобы график функции у=f(x)

ТЕОРЕМА 38. Для того чтобы график функции у=f(x) имел при х→+∞

имел при х→+∞ наклонную асимптоту Y=kx+b необходимо и достаточно,

чтобы существовали пределы




Пример

Слайд 5
Для дробно рациональной функции:
Асимптоты на +∞ и −

Для дробно рациональной функции:Асимптоты на +∞ и − ∞ одновременно существуют

∞ одновременно существуют или не существуют и в первом

случае совпадают.
Если степень знаменателя выше степени числителя, то асимптота нулевая.
Если степень знаменателя равна степени числителя, то асимптота горизонтальная.
Если степень знаменателя на 1 ниже степени числителя, то существует наклонная асимптота.
Если разность степеней больше 1, то наклонных асимптот не существует.

Слайд 6 ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
Элементарное исследование
- область определения, непрерывность,

ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИЭлементарное исследование- область определения, непрерывность, точки разрыва, их

точки разрыва, их тип (вертикальные асимптоты);
- четность, периодичность
- точки

пересечения с осями;
наклонные асимптоты;
точки пересечения с асимптотами

Слайд 7
2. Промежутки возрастания, убывания, точки экстремума.
3. Промежутки выпуклости,

2. Промежутки возрастания, убывания, точки экстремума.3. Промежутки выпуклости, вогнутости, точки перегиба.Пример.

вогнутости, точки перегиба.

Пример.

  • Имя файла: asimptoty-grafika-funktsii.pptx
  • Количество просмотров: 122
  • Количество скачиваний: 1
- Предыдущая Достопримечательности города Бутурлиновка
Следующая - Трудовая миграция населения Республики Хорватия

Похожие презентации

Презентация по теме: Показательная функция и её применение в природе и технике Презентация по теме: Показательная функция и её применение в природе и технике 138
Табличное умножение и деление Устный счёт Табличное умножение и деление Устный счёт 98
Презентация по математике на темуИсследовательская деятельность как одно из направлений работы с учащимися в условиях реализации ФГОС. Презентация по математике на темуИсследовательская деятельность как одно из направлений работы с учащимися в условиях реализации ФГОС. 93
Презентация презентация к уроку по математике (4 класс) Презентация презентация к уроку по математике (4 класс) 108
Презентация Связь между компонентами сложения 1 класс презентация к уроку по математике (1 класс) по теме Презентация Связь между компонентами сложения 1 класс презентация к уроку по математике (1 класс) по теме 106
Тренажёр по математике для 2 класса Решение задач тренажёр по математике (2 класс) Тренажёр по математике для 2 класса Решение задач тренажёр по математике (2 класс) 146
Дидактическая игра на тему ВПР Оценка размеров реальных объектов Дидактическая игра на тему ВПР Оценка размеров реальных объектов 158
Прибавление числа 2. Закрепление пройденного Прибавление числа 2. Закрепление пройденного 107
Считалка для ворон Считалка для ворон 112
Презентация по математике на тему Степень числа (5 класс) Презентация по математике на тему Степень числа (5 класс) 145
Умножение дробей, нахождение дроби от числа, применение распределительного свойства умножения Умножение дробей, нахождение дроби от числа, применение распределительного свойства умножения 125
Из чего строится геометрия? Из чего строится геометрия? 162
Дифференцирование частного и степени Дифференцирование частного и степени 80
Проект по математике Золотое сечение Проект по математике Золотое сечение 149
Презентация по наглядной геометрии по теме: Углы Презентация по наглядной геометрии по теме: Углы 144
алгоритм написания цифры от 0-9 презентация к уроку по математике (1 класс) алгоритм написания цифры от 0-9 презентация к уроку по математике (1 класс) 129
Сумма углов треугольника Сумма углов треугольника 112
Пифагор и его теорема (10 класс) Пифагор и его теорема (10 класс) 94
Презентация для внеклассного мероприятия Математики. Какие они бывают? Презентация для внеклассного мероприятия Математики. Какие они бывают? 119
Трудные случаи таблицы умножения и деления Трудные случаи таблицы умножения и деления 104
Математические софизмы Математические софизмы 118
Устный счёт презентация к уроку по математике Устный счёт презентация к уроку по математике 111
ustnyy schet 3 klass kak kormit drakona ustnyy schet 3 klass kak kormit drakona 133
Математическая таблица презентация к уроку по математике (2 класс) Математическая таблица презентация к уроку по математике (2 класс) 113
Презентация к уроку внеурочной деятельности Отрезок. Имя отрезка Презентация к уроку внеурочной деятельности Отрезок. Имя отрезка 150
Первые шаги в геометрии Первые шаги в геометрии 114
Числовые выражения Числовые выражения 150
Математический диктант презентация к уроку по математике Математический диктант презентация к уроку по математике 128
Презентация: Периметр многоугольника презентация к уроку по математике (3 класс) по теме Презентация: Периметр многоугольника презентация к уроку по математике (3 класс) по теме 135
Презентация по математике на тему Устный счет (4 класс, часть 3) Презентация по математике на тему Устный счет (4 класс, часть 3) 163