- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Аттестационная работа. Разработка урока Решение задач на применение второго признака равенства треугольников 7 класс
Содержание
- 2. ЦЕЛЬ РАЗРАБОТКИ:Совершенствовать навыки решения задач на применение второго признака равенства треугольников.
- 3. МАТЕМАТИЧЕСКИЙ ДИКТАНТНайдите на рисунках треугольники, равные по
- 4. МАТЕМАТИЧЕСКИЙ ДИКТАНТ
- 5. ПРОВЕРЬ СЕБЯПо двум сторонам и углу между
- 6. 1. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ:В четырехугольнике
- 7. Отрезки АВ и CD пересекаются в точке
- 8. 1. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ:Лучи AD
- 9. ИСТОРИЧЕСКАЯ СПРАВКА О ПРИЗНАКАХ РАВЕНСТВА ТРЕУГОЛЬНИКОВСейчас в
- 10. Признаки равенства треугольников имели издавна важнейшее значение
- 11. Предполагают, что его способ состоял в следующем:
- 12. РАБОТА В ПАРАХ: На рисунке дана фигура,
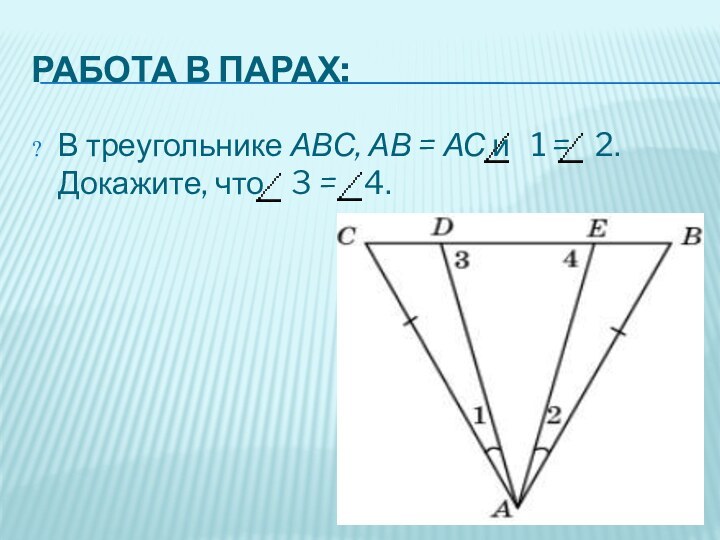
- 13. РАБОТА В ПАРАХ: В треугольнике АВС, АВ
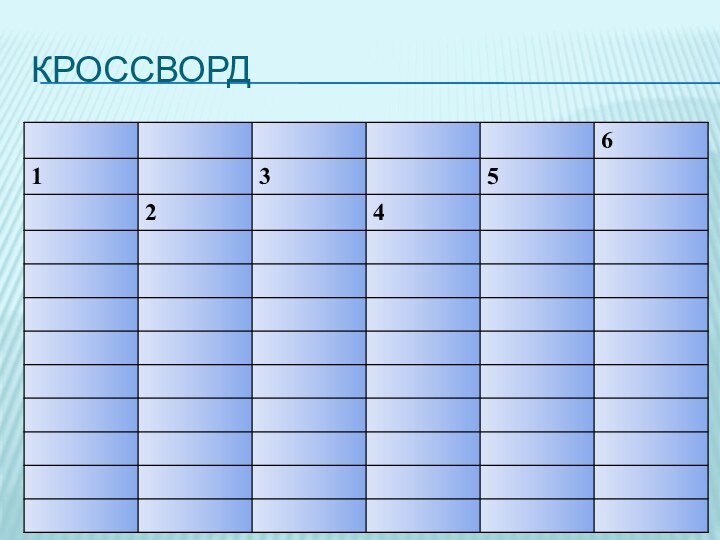
- 14. КРОССВОРД: 1. Как называется отрезок, соединяющий
- 15. КРОССВОРД
- 16. КРОССВОРД
- 17. КРОССВОРД
- 18. Для доказательства равенства треугольников ABC и MNK достаточно доказать, что: a )AC = MN; 5)
- 19. Чтобы доказать равенство равносторонних треугольников ABC и MNK, достаточно доказать, что:а)
- 20. Скачать презентацию
- 21. Похожие презентации
ЦЕЛЬ РАЗРАБОТКИ:Совершенствовать навыки решения задач на применение второго признака равенства треугольников.










Слайд 2
ЦЕЛЬ РАЗРАБОТКИ:
Совершенствовать навыки решения задач на применение второго
признака равенства треугольников.
Слайд 3
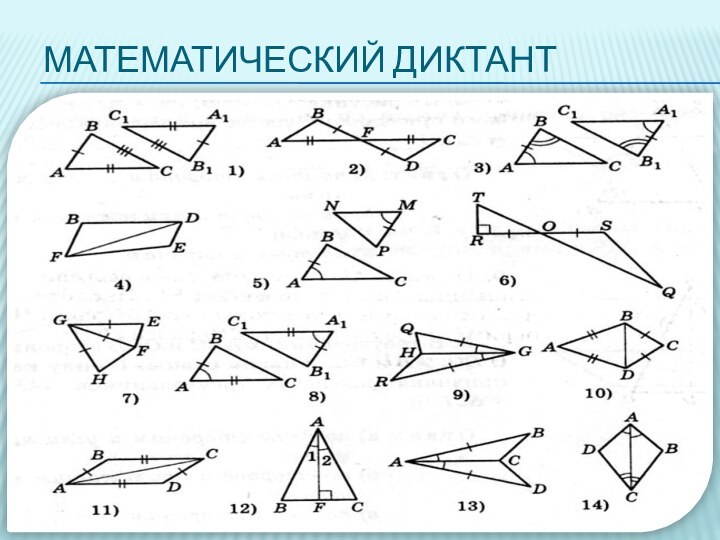
МАТЕМАТИЧЕСКИЙ ДИКТАНТ
Найдите на рисунках треугольники, равные по первому,
второму признакам равенства треугольников.
Укажите номера этих треугольников в ответе.
Слайд 5
ПРОВЕРЬ СЕБЯ
По двум сторонам и углу между ними:
2,
8, 9, 13.
По стороне и прилежащим к ней углам:
3,
6, 12, 14.
Слайд 6
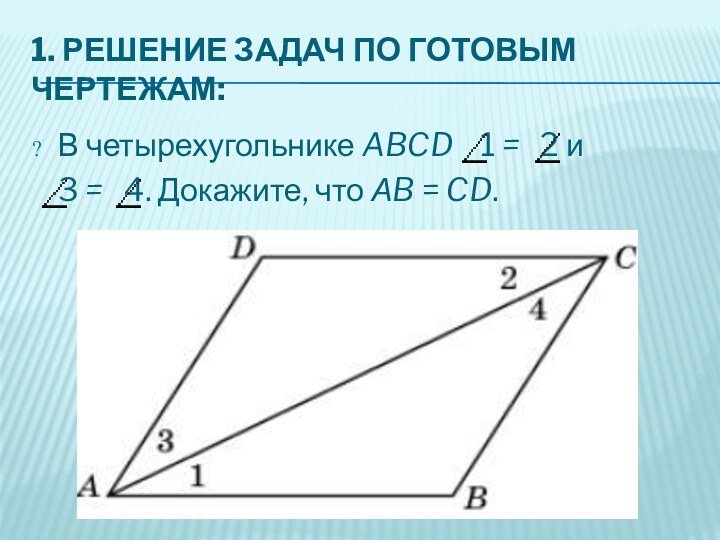
1. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ:
В четырехугольнике ABCD
1 = 2 и
3 =
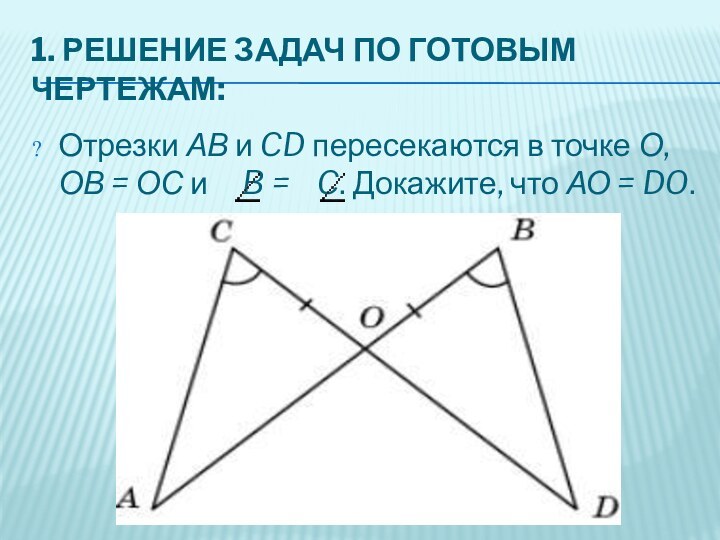
4. Докажите, что АB = CD.Слайд 7 Отрезки АВ и CD пересекаются в точке О,
ОВ = ОС и B =
C. Докажите, что АО = DO.1. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ:
Слайд 8
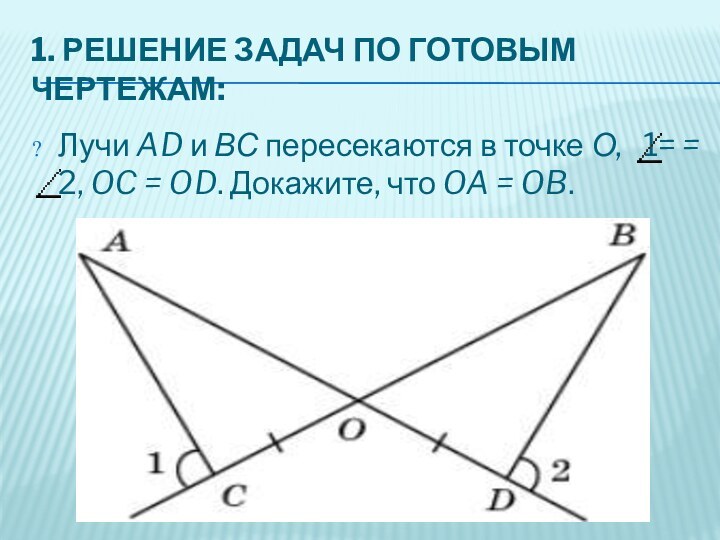
1. РЕШЕНИЕ ЗАДАЧ ПО ГОТОВЫМ ЧЕРТЕЖАМ:
Лучи AD и
ВС пересекаются в точке О, 1= =
2, OC = OD. Докажите, что OA = OB.
Слайд 9
ИСТОРИЧЕСКАЯ СПРАВКА О ПРИЗНАКАХ РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Сейчас в своей
работе вы использовали такой приём, как доказательство. Эта форма
работы вам ещё недостаточно известна. А до VI века н.э. с доказательством люди вообще были не знакомы.Первым учёным, который стал рассуждать, доказывать, был Фалес Милетский. Фалес считается одним из семи мудрецов, оказавших большое влияние на жизнь древних греков. Одним из самых известных его высказываний было «Познай самого себя».
Слайд 10 Признаки равенства треугольников имели издавна важнейшее значение в
геометрии, так как доказательства многочисленных теорем сводилось к доказательству
равенства тех или иных треугольников.Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).
Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно.
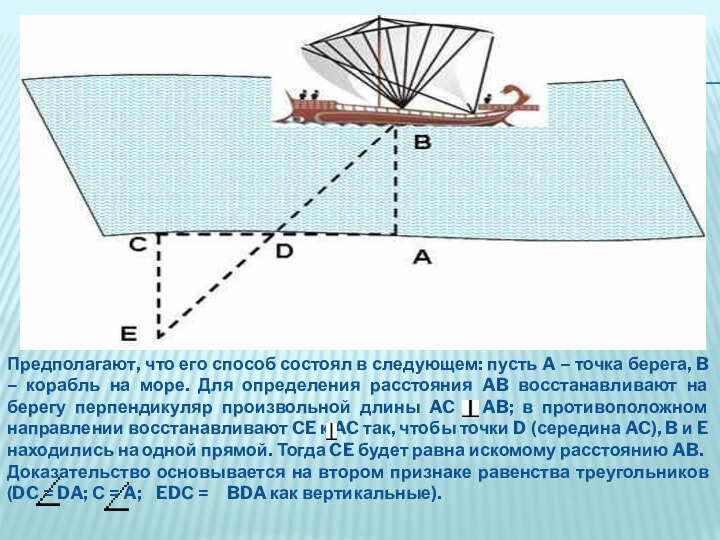
Слайд 11 Предполагают, что его способ состоял в следующем: пусть
A – точка берега, B – корабль на море.
Для определения расстояния AB восстанавливают на берегу перпендикуляр произвольной длины AC к AB; в противоположном направлении восстанавливают CE к AC так, чтобы точки D (середина AC), B и E находились на одной прямой. Тогда CE будет равна искомому расстоянию AB.Доказательство основывается на втором признаке равенства треугольников (DC = DA; С = A; EDС = BDA как вертикальные).
Слайд 12
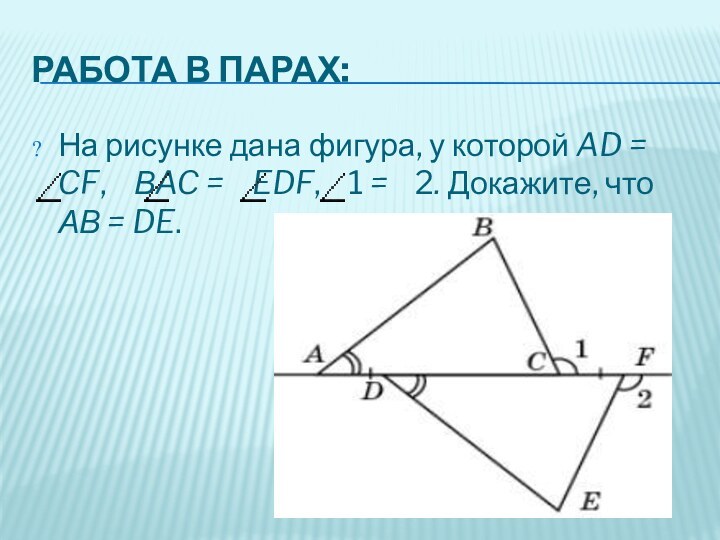
РАБОТА В ПАРАХ:
На рисунке дана фигура, у
которой AD = CF, ВAC = EDF,
1 = 2. Докажите, что АВ = DE.
Слайд 14
КРОССВОРД:
1. Как называется отрезок, соединяющий вершину треугольника
с серединой противоположной стороны?
2. Как называется перпендикуляр, опущенный из
вершины треугольника на прямую, содержащую противоположную сторону?3. Замкнутая линия, состоящая из множества точек, равноудаленных от центра?
4. Часть прямой, ограниченная точкой?
5. Как называется луч, выходящий из вершины угла и делящий его пополам?
6. Отрезок, соединяющий центр окружности с точкой, лежащей на окружности?( ключевое слово –ЕВКЛИД)
Слайд 18
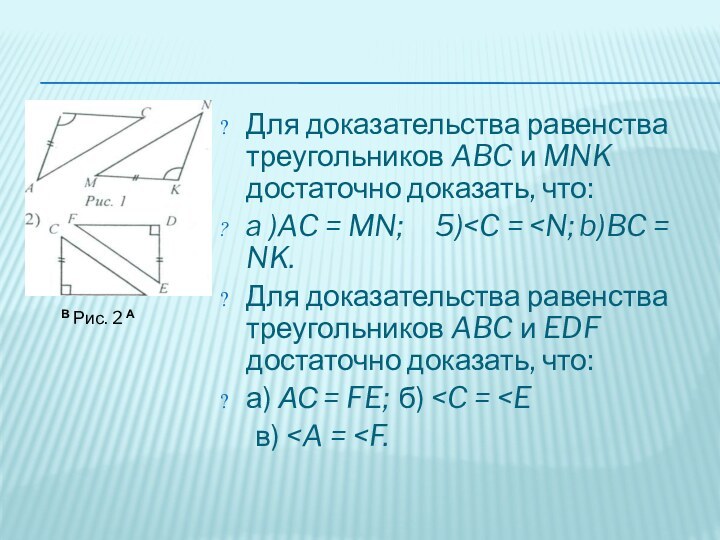
Для доказательства равенства треугольников ABC и MNK достаточно
доказать, что:
a )AC = MN; 5)
NK.Для доказательства равенства треугольников ABC и EDF достаточно доказать, что:
а) АС = FE; б)
В Рис. 2 А
Слайд 19
Чтобы доказать равенство равносторонних треугольников ABC и MNK,
достаточно доказать, что:
а)
= РМNК.Рис. 3 К
Выберите верное утверждение:
а) ВС = КМ; б) АВ = KN; в) ВС = NM.





























