- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Calculating the probability of a continuous random variable – Normal Distribution. Week 9 (1)
Содержание
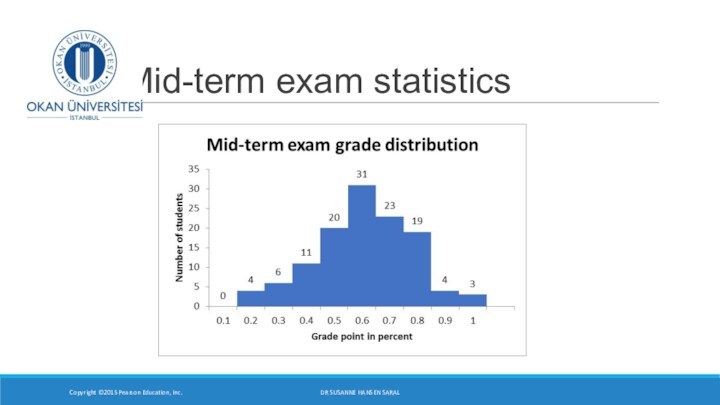
- 2. Mid-term exam statisticsCopyright ©2015 Pearson Education, Inc.DR SUSANNE HANSEN SARAL
- 3. Copyright ©2015 Pearson Education, Inc.DR SUSANNE HANSEN SARAL Mid-term exam statistics
- 4. Continuous random variableA continuous random variable can
- 5. Calculating probabilities of continuous random
- 6. COPYRIGHT © 2013
- 7. Procedure for calculating the probability of x
- 8. Procedure for calculating the probability of
- 9. Using the Standard Normal TableCopyright ©2015 Pearson
- 10. P(z < +
- 11. DR SUSANNE HANSEN SARALZ0-1.00Z01.00.8413.1587.8413.1587
- 13. Determine for shampoo filling machine 1 the proportion of bottles that:
- 14.
- 15. Solution: Contain more than 505 ml
- 16. P ( z < + 1.05) =P
- 17. P (
- 18. Haynes Construction Company
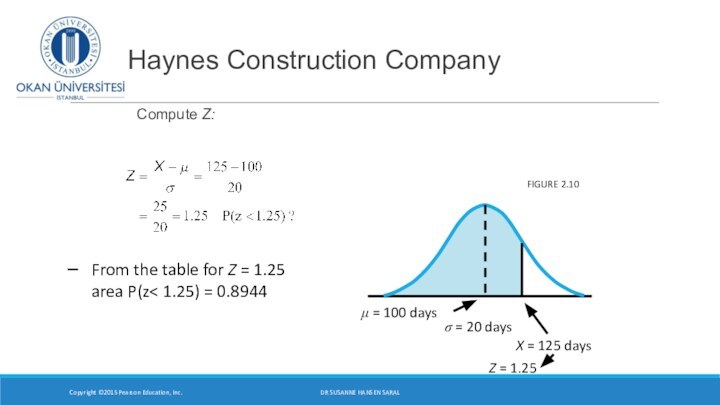
- 19. Haynes Construction Company Compute Z:Copyright ©2015 Pearson
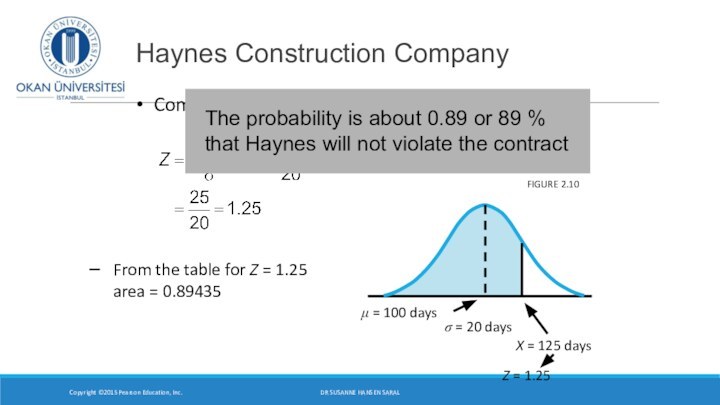
- 20. Compute Z Haynes Construction Company Copyright ©2015 Pearson
- 21. Haynes Construction Company Copyright ©2015 Pearson Education, Inc.FIGURE 2.10P(z > 1.25) DR SUSANNE HANSEN SARAL
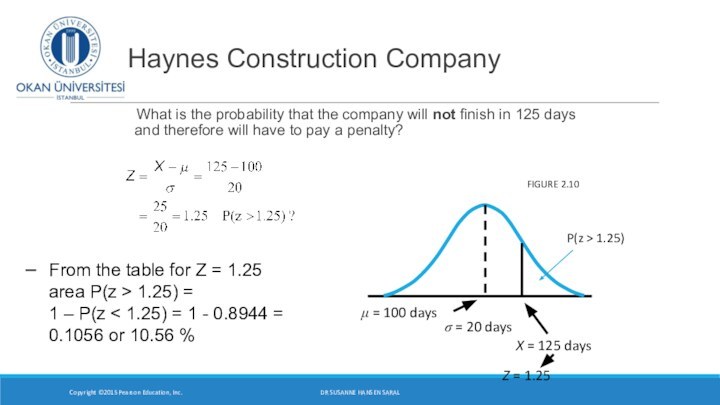
- 22. Haynes Construction Company What is the probability
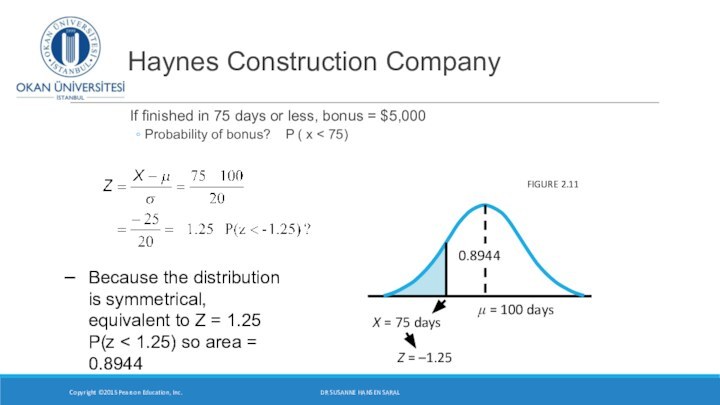
- 23. Haynes Construction Company If finished in 75
- 24. Haynes Construction Company If finished in 75
- 25. If finished in 75 days or less,
- 26. Haynes Construction Company Probability of completing between
- 27. Haynes Construction Company Probability of completing between
- 28. Haynes Construction Company Probability of completing between
- 29. Скачать презентацию
- 30. Похожие презентации



















Слайд 4
Continuous random variable
A continuous random variable can assume
any value in an interval on the real line
or in a collection of intervals.It is not possible to talk about the probability of the random variable assuming a particular value, because the probability will be close to 0.
Instead, we talk about the probability of the random variable assuming a value within a given interval.
Copyright ©2015 Pearson Education, Inc.
DR SUSANNE HANSEN SARAL
Слайд 5
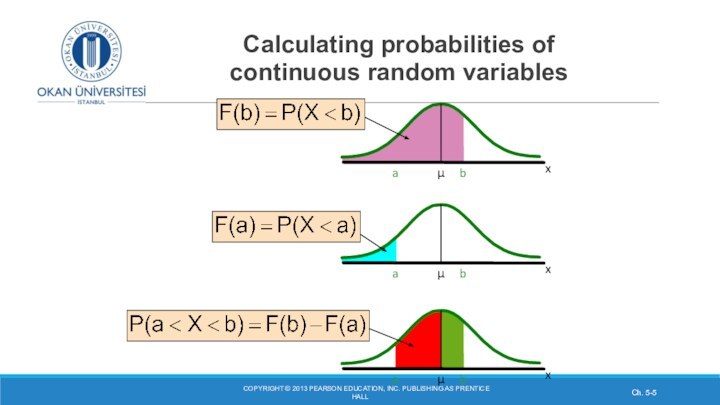
Calculating probabilities of
continuous random variables
COPYRIGHT © 2013 PEARSON EDUCATION, INC.
PUBLISHING AS PRENTICE HALLCh. 5-
x
b
μ
a
x
b
μ
a
x
b
μ
a
Слайд 6 COPYRIGHT © 2013 PEARSON
EDUCATION, INC. PUBLISHING AS PRENTICE HALL
Ch. 5-
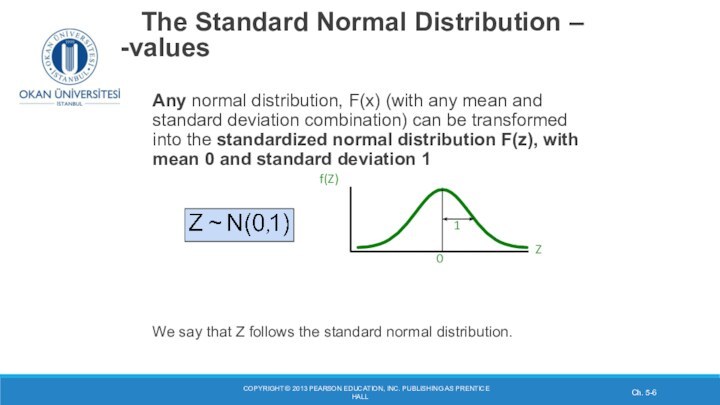
The Standard Normal Distribution – z-valuesAny normal distribution, F(x) (with any mean and standard deviation combination) can be transformed into the standardized normal distribution F(z), with mean 0 and standard deviation 1
We say that Z follows the standard normal distribution.
Z
f(Z)
0
1
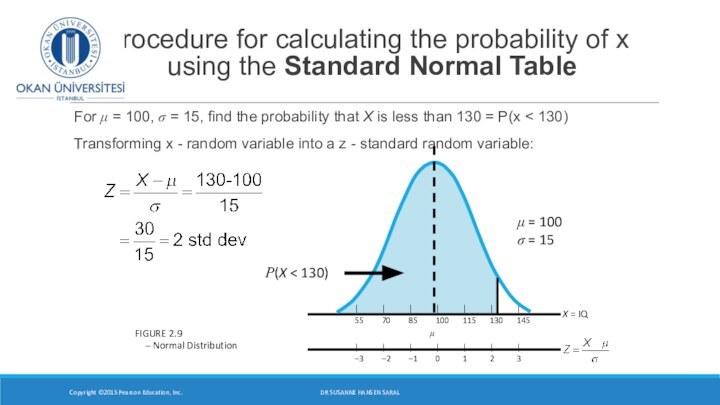
Слайд 7 Procedure for calculating the probability of x
using the Standard Normal Table
For
μ = 100, σ = 15, find the probability that X is less than 130 = P(x < 130)Transforming x - random variable into a z - standard random variable:
Copyright ©2015 Pearson Education, Inc.
FIGURE 2.9
– Normal Distribution
DR SUSANNE HANSEN SARAL
Слайд 8 Procedure for calculating the probability of x
using the Standard Normal
Table (continued)Step 2
Look up the probability from the table of normal curve areas
Column on the left is Z value
Row at the top has second decimal places for Z values
Copyright ©2015 Pearson Education, Inc.
DR SUSANNE HANSEN SARAL
Слайд 9
Using the Standard Normal Table
Copyright ©2015 Pearson Education,
Inc.
TABLE 2.10 – Standardized Normal Distribution (partial)
For Z =
2.00P(X < 130) = P(Z < 2.00) = 0.97725
P(X > 130) = 1 – P(X ≤ 130) = 1 – P(Z ≤ 2)
= 1 – 0.97725 = 0.02275
DR SUSANNE HANSEN SARAL
Слайд 10 P(z < + 2)
= P(z > -2) = .9772
In probability terms, a
z-score of -2.0 and +2.0 has the same probability, because they are mirror images of each other.If we look for the z-score 2.0 in the table we find a value of 9772.
Copyright ©2015 Pearson Education, Inc.
DR SUSANNE HANSEN SARAL
Слайд 11
DR SUSANNE HANSEN SARAL
Z
0
-1.00
Z
0
1.00
.8413
.1587
.8413
.1587
The Standard Normal Table
Copyright ©2015 Pearson Education, Inc.
P( z
< - 1.0) = 1 - .8413 = 0.1587 To find the probability of: P (z > 1) and P (z < -1) we will use the complement rule:
P( z > 1.0) = 1 - .8413 = 0.1587
Слайд 12
Finding the probability of z-scores
with two decimals and graph the probability P ( z < + 0.55) = 0.7088 or 70.88 %
P (z > + .55) = 1.0 – 0.7088 = 0.2912 or 29.12%
P ( z > - 0.55) = 0.7088 or 70.88 %
P ( z < - 0.55) = 1.0 - .7088 = 0.2912 or 29.12 %
P ( z < + 1.65) = 0.9505 or 95.05 %
P (z > + 1.65) = 1.0 – 0.9505 = 0.0495 or 4.96 %
P( z > - 2.36) = .9909 or 99.09 %
P ( z < + 2.36) = .9909 or 99.09 %
Copyright ©2015 Pearson Education, Inc.
DR SUSANNE HANSEN SARAL
Слайд 16
P ( z < + 1.05) =
P (z
> -1.05 ) =
P (z < - 3.34) =
P (z > - 3.34) =
P (z > - 2.47) =
P (z < + 1.87) =
P (z > + 2.57) =
P ( z < - 0.32) =
Copyright ©2015 Pearson Education, Inc.
DR SUSANNE HANSEN SARAL
Слайд 17
P ( z
< + 1.05) = 0.8531 or 85.31 %
P (z
> -1.05 ) = 0.8531 or 85.31 %P (z < - 3.34) = 1.0 – 0.9996 = 0.0004 or 0.04 %
P (z > - 3.34) = 0.9996 or 99.96 %
P (z > - 2.47) = 0.9932 or 99.32 %
P (z < + 1.87) = 0.9693 or 96.93 %
P (z > + 2.57) = 1.0 – 0.9949 = 0.0054 or 0.054 %
P( z < - 0.32) = 1.0 – 0.6255 = 0.3745 or 37. 45 %
Exercise:
Find the probability of z-scores
and draw a graph of the probability
Copyright ©2015 Pearson Education, Inc.
DR SUSANNE HANSEN SARAL
Слайд 18 Haynes Construction Company
Example
Copyright ©2015 Pearson Education, Inc.
FIGURE 2.10
DR SUSANNE
HANSEN SARAL
Слайд 19
Haynes Construction Company
Compute Z:
Copyright ©2015 Pearson Education,
Inc.
FIGURE 2.10
From the table for Z = 1.25
area P(z
1.25) = 0.8944DR SUSANNE HANSEN SARAL
Слайд 20
Compute Z
Haynes Construction Company
Copyright ©2015 Pearson Education,
Inc.
FIGURE 2.10
From the table for Z = 1.25
area =
0.89435The probability is about 0.89 or 89 %
that Haynes will not violate the contract
DR SUSANNE HANSEN SARAL
Слайд 21
Haynes Construction Company
Copyright ©2015 Pearson Education, Inc.
FIGURE
2.10
P(z > 1.25)
DR SUSANNE HANSEN SARAL
Слайд 22
Haynes Construction Company
What is the probability that
the company will not finish in 125 days and
therefore will have to pay a penalty?Copyright ©2015 Pearson Education, Inc.
FIGURE 2.10
From the table for Z = 1.25
area P(z > 1.25) =
1 – P(z < 1.25) = 1 - 0.8944 =
0.1056 or 10.56 %
P(z > 1.25)
DR SUSANNE HANSEN SARAL
Слайд 23
Haynes Construction Company
If finished in 75 days
or less, Haynes will get a bonus of $5,000
What
is the probability of a bonus? P ( x < 75) Copyright ©2015 Pearson Education, Inc.
DR SUSANNE HANSEN SARAL
Слайд 24
Haynes Construction Company
If finished in 75 days
or less, bonus = $5,000
Probability of bonus? P
( x < 75) Copyright ©2015 Pearson Education, Inc.
FIGURE 2.11
Because the distribution is symmetrical, equivalent to Z = 1.25
P(z < 1.25) so area = 0.8944
0.8944
DR SUSANNE HANSEN SARAL
Слайд 25 If finished in 75 days or less, bonus
= $5,000
Probability of bonus?
Haynes Construction Company
Copyright ©2015 Pearson
Education, Inc.FIGURE 2.11
P(z < -1.25) = 1.0 – P(z < 1.25)
= 1.0 – 0.8944 = 0.1056
The probability of completing the contract in 75 days or less is about 11%
Because the distribution is symmetrical, equivalent to Z = 1.25
so area = 0.89435
0.8944
DR SUSANNE HANSEN SARAL
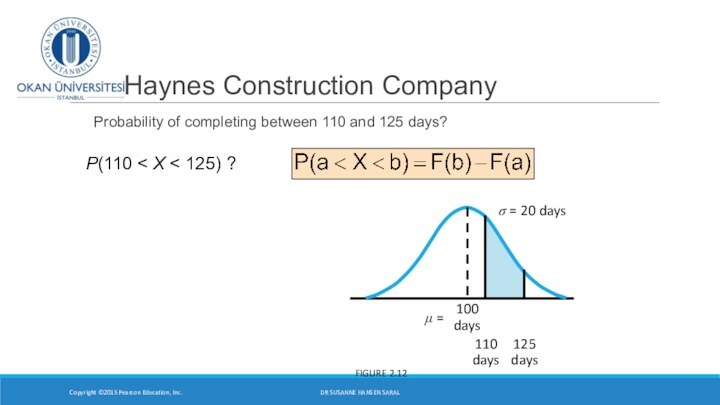
Слайд 26
Haynes Construction Company
Probability of completing between 110
and 125 days?
Copyright ©2015 Pearson Education, Inc.
FIGURE 2.12
P(110
X < 125) ? DR SUSANNE HANSEN SARAL
Слайд 27
Haynes Construction Company
Probability of completing between 110
and 125 days?
Copyright ©2015 Pearson Education, Inc.
FIGURE 2.12
P(110
X < 125) ? DR SUSANNE HANSEN SARAL
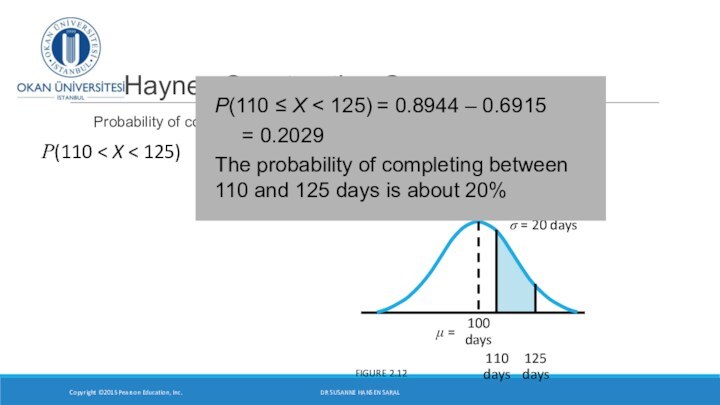
Слайд 28
Haynes Construction Company
Probability of completing between 110
and 125 days?
Copyright ©2015 Pearson Education, Inc.
FIGURE 2.12
P(110
X < 125) P(110 ≤ X < 125) = 0.8944 – 0.6915
= 0.2029
The probability of completing between 110 and 125 days is about 20%
DR SUSANNE HANSEN SARAL





























