- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Система счисления (6 класс)
Содержание
- 2. Система счисления – это способы записи чисел
- 4. Позиционные системы счисленияВ позиционных системах счисления количественное
- 5. Непозиционные системы счисленияВ непозиционных системах счисления величина,
- 6. Счёт у первобытных народов
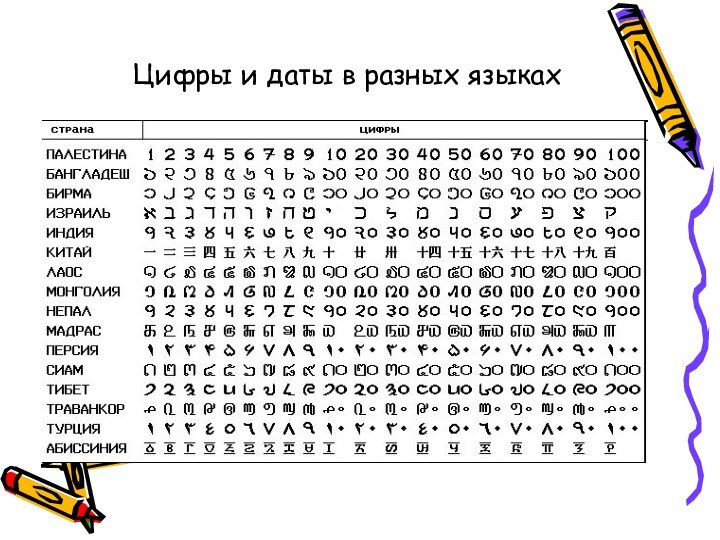
- 8. Цифры и даты в разных языках
- 9. Древние римляне пользовались нумерацией, сохраняющейся
- 10. Первые 12 чисел записываются в римских цифрах
- 11. Каноническим примером фактически непозиционной системы счисления
- 12. Греческая система счисленияГреческая система счисления, также известная
- 13. Алфавитные системы счисленияБолее совершенными непозиционными системами счисления
- 14. Десятичная система счисленияДля мультипликативной системы нужно знать
- 15. Славянская система счисления
- 16. Древние системы счисления
- 17. Что осталось от древних систем счисления?Римский цифры
- 18. Что осталось от древних систем счисления?До тридцатых
- 19. Дюжина достаточно прочно вошла в нашу жизнь:
- 20. Скачать презентацию
- 21. Похожие презентации
Система счисления – это способы записи чисел в виде, удобном для прочтения и выполнения арифметических операций. Рассматривая археологические находки эпохи палеолита (камни, кости животных), можно заметить, что люди стремились группировать точки, полосы и насечки по 3,



















Слайд 4
Позиционные системы счисления
В позиционных системах счисления количественное значение
цифры зависит от ее позиции в числе.
Позиция цифры в
числе называется разрядом.Каждая позиционная сс имеет определенный алфавит цифр и основание.
Слайд 5
Непозиционные системы счисления
В непозиционных системах счисления величина, которую
обозначает цифра, не зависит от положения в числе. При
этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
Слайд 7
Развитие понятия числа – появления нуля и
отрицательных чисел, обыкновенных и десятичных дробей, способы записи чисел
(цифры, обозначения системы счисления) – всё это имеет богатую и интересную историю.
Слайд 9
Древние римляне пользовались нумерацией, сохраняющейся до настоящего времени
под именем "римской нумерации", в которой числа изображаются буквами
латинского алфавита. Сейчас ею, строф в стихотворениях и т.д. В позднейшем своем виде пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах римские цифры выглядят так:I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000.
Слайд 10
Первые 12 чисел записываются в римских цифрах так:
I,
II, III, IV, V, VI, VII, VIII. IX, X,
XI, XII.Другие же числа записываются, например, как:
XXVIII = 28; ХХХIХ = 39; CCCXCVII = 397; MDCCCXVIII = 1818.
Слайд 11
Каноническим примером фактически непозиционной системы счисления является
римская, в которой в качестве цифр используются латинские буквы:
I
- 1,V - 5,
X - 10,
L - 50,
C - 100,
D - 500,
M - 1000
Римская система счисления
Слайд 12
Греческая система счисления
Греческая система счисления, также известная как
ионийская или новогреческая — непозиционная система счисления, в которой,
в качестве символов для счёта, употребляют греческие буквы, а также дополнительные символы, такие как ς (стигма), Ϙ (копа) и Ϡ (сампи).Эта система пришла на смену аттической, или старогреческой, системе, которая господствовала в Греции в III веке до н.э..
Необходимость сохранять порядок букв ради сохранения их числовых значений привела к относительно ранней (4 век до н.э.) стабилизации греческого алфавита.
1 α 10 ι 100 ρ
2 β 20 κ 200 σ Данные числа позволяют записать числа
3 γ 30 λ 300 τ лишь от 1 до 999, например:
4 δ 40 μ 400 υ 45 — με
5 ε 50 ν 500 φ 632 — χλβ
6 ς 60 ξ 600 χ 970 — Ϡο
7 ζ 70 ο 700 ψ
8 η 80 π 800 ω
9 θ 90 Ϙ 900 Ϡ
Слайд 13
Алфавитные системы счисления
Более совершенными непозиционными системами счисления были
алфавитные системы. К числу таких систем счисления относились греческая,
славянская, финикийская и другие. В них числа от 1 до 9, целые количества десятков (от 10 до 90) и целые количества сотен (от 100 до 900) обозначались буквами алфавита. В алфавитной системе счисления Древней Греции числа 1, 2, ..., 9 обозначались первыми девятью буквами греческого алфавита, и т.д. Для обозначения чисел 10, 20, ..., 90 применялись следующие 9 букв а для обозначения чисел 100, 200, ..., 900 – последние 9 букв.У славянских народов числовые значения букв установились в порядке славянского алфавита, который использовал сначала глаголицу, а затем кириллицу.
В России славянская нумерация сохранилась до конца XVII века. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранилась только в богослужебных книгах.
Слайд 14
Десятичная система счисления
Для мультипликативной системы нужно знать изображение
цифр и их значение, а так же основание системы
счисления. Определить основание очень легко, нужно только пересчитать количество значащих цифр в системе. Если проще, то это число, с которого начинается второй разряд у числа. Мы, например, используем цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Их ровно 10, поэтому основание нашей системы счисления тоже 10, и система счисления называется “десятичная”. В вышеприведенном примере используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (вспомогательные 10, 100, 1000, 10000 и т. д. не в счет). Основных цифр здесь тоже 10, и система счисления – десятичная.
Слайд 17
Что осталось от древних систем счисления?
Римский цифры до
сих пор используются в некоторых случаях, например, на циферблате
часов или в книгах для нумерации глав и страниц вступления.Древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60. Остатки шестидесятеричной системы счисления мы находим, в сохранившемся до наших дней, обыкновении делить час на 60 минут, а минуту на 60 секунд и градус на 60 минут .
Слайд 18
Что осталось от древних систем счисления?
До тридцатых годов
ХХ в. широкое распространение имели элементы 12-чной системы счисления
в Европе (еще в XIXв. в России был в обиходе денежный знак “империал” с номинальной стоимостью 36 рублей и в Англии фунт равнялся 12 шиллингам, а шиллинг – 12 пенсам).Слайд 19 Дюжина достаточно прочно вошла в нашу жизнь: в
сутках две дюжины часов, где час делится на пять
дюжин минут, круг содержит тридцать дюжин градусов, фут делится на двенадцать дюймов. Влияние 12-чной системы счисления ощущается сегодня хотя бы в том, что карандашей или фломастеров в наборе обычно бывает 6, 12, 24 и т.д.Нередко и мы сталкиваемся в быту с двенадцатеричной системой счисления: чайные и столовые сервизы на 12 персон, комплект платков - 12 штук
Проанализировав счет в различных иностранных языках, мы обнаружили, что в большинстве случаев используется десятеричная система счисления (русский, немецкий, испанский, польский, болгарский и др.), но присутствуют также и другие: двенадцатеричная – английский язык и двадцатеричная – французский язык.
Что осталось от древних систем счисления?