Презентация на тему Четырехугольники

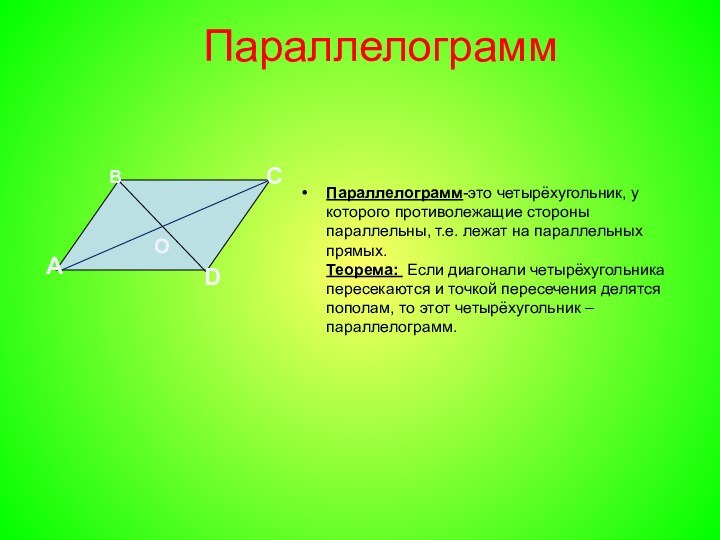
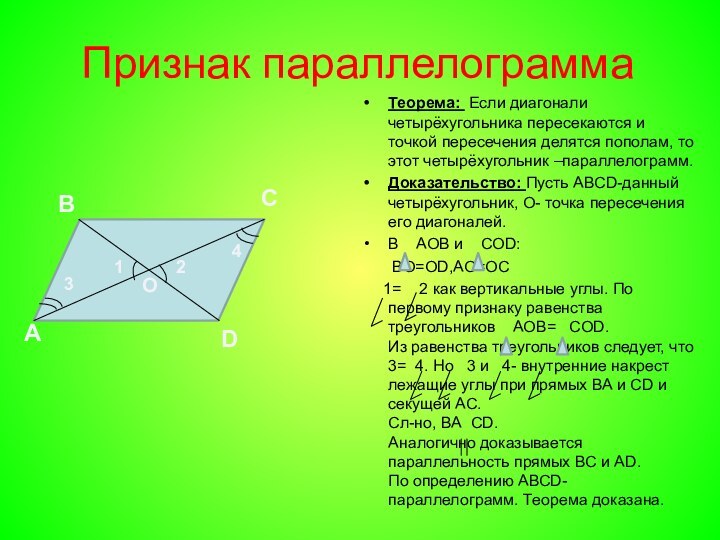
лежат на параллельных прямых. Теорема: Если диагонали четырёхугольника пересекаются и

точкой пересечения делятся пополам, то этот четырёхугольник –параллелограмм.

В

А

С

D

O

пересечения делятся пополам, то этот четырёхугольник –параллелограмм.
Доказательство: Пусть АВСD-данный

четырёхугольник, О- точка пересечения его диагоналей.
В АОВ и СОD:
BO=OD,AO=OС
1= 2 как вертикальные углы. По первому признаку равенства треугольников AOB= COD. Из равенства треугольников следует, что 3= 4. Но 3 и 4- внутренние накрест лежащие углы при прямых ВА и СD и секущей АС. Сл-но, ВА CD. Аналогично доказывается параллельность прямых ВС и АD. По определению АВСD-параллелограмм. Теорема доказана.

В

С

D

O

1

2

3

4

А

пересечения деля-тся пополам.
Доказательство:
АВС1D –параллелограмм

ВС1 АD = BС1=BС DС1 АВ= DС1= DС т.е. АВС1D =АВС откуда следует, что АО=DС, ВО=DО, что и требовалось доказать. Теорема доказана.

В

С

А

D

O

С

1

прямые.

Теорема: Диагонали прямоугольника равны.

С

В

А

D

данный прямоугольник. Утверждение теоремы следует из равенства прямоугольных треугольников

ВАD и СD А. У них углы ВАD и СDА прямые. Катет АD общий, А катеты АВ и СD равны как противолежащие стороны параллелограмма. Из равенства треугольников следует, что их гипотенузы равны. А гипотенузы есть диагонали прямоугольника. Теорема доказана.

С

В

А

D

равны.
Теорема: Диагонали ромба пересекаются под прямым углом. Диагонали ромба

являются биссектрисой его углов.

А

В

С

D

углом. Диагонали ромба являются биссектрисой его углов.
Доказательство: Пусть АВСD

– данный ромб, О –точка пересечения его диагоналей. По свойству параллелограмма АО=ОС. Значит, в треугольнике АВС отрезок ВО является медианой. Так как АВСD – ромб, то АВ=ВС и треугольник АВС равнобедренный.
По свойству равнобедренного треугольника медиана, проведённая к его основанию, является и биссектрисой и высотой. А это значит, что диагональ ВD является биссектрисой угла В и перпендикулярна диагонали АС. Теорема доказана.

С

D

А

В

O