Презентация на тему Числа Бернулли

трудами ее ученых и

ценностью ее открытий»
Л.Пастер

как таковых так и их свойств и поведения в

различных ситуациях.
Как сказал великий математик Пифагор "Все есть число!“
Изучая числа мы изучаем окружающий нас мир и себя в том числе. С древних времен математики пытались постичь тайны удивительного мира чисел. Этот мир привлекает своим многообразием, строгостью и совершенством законов.
Здесь есть «великаны» и есть «карлики», обычные «трудяги» и такие «знаменитости», как π и e.

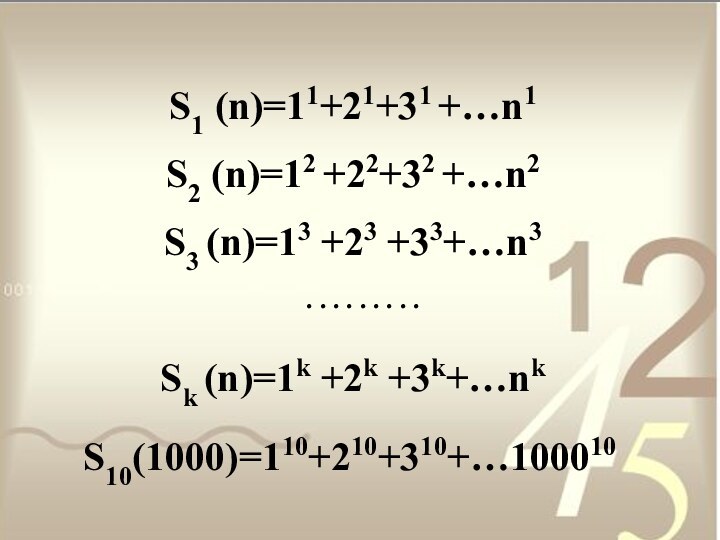
Числа Бернулли.

«Прогресс науки определяется трудами ее ученых и ценностью их открытий» Л.Пастер

и последовательность натуральных чисел и полная глубоких тайн последовательность

простых чисел и последовательность “биноминальных коэффициентов”…
В моей работе речь пойдет об одной замечательной последовательности чисел, которую открыл выдающийся швейцарский математик Якоб Бернулли (1654—1705).Последовательность эта играет в математике важную роль, что объясняется ее связью с вопросами суммирования функций, простыми числами, великой теоремой Ферма, а также другими задачами.

Отец не допускал отступления от намеченного плана, поэтому Якоб

вынужден был заниматься математикой тайком, без учителя и почти без учебников.
Обучение в университете шло своим чередом, и в 1671г. он получил степень магистра философии. В 1676 Якоб отправился в длительное путешествие, из которого возвратился только в 1680г. Он посетил некоторые города Швейцарии, Италию, Францию.

и 1682 две работы: одна содержала рассуждения о природе

комет, другая - о тяжести эфира. Наиболее значительные достижения Якоба I в развитии анализа бесконечно малых, теории рядов, вариационного исчисления и теории вероятностей.
В 1687, ознакомившись с первым мемуарам Г.Лейбница по дифференциальному исчислению (1684), применил новые идеи к изучению свойств ряда кривых: логарифмические спирали, открытой им лемнискаты, цепной линии и др.
В труде "Искусство предложения" Якоб I в 1713 решил некоторые задачи комбинаторики; открыл числа, позднее названные числа Бернулли; доказал так называемую теорему Бернулли - частный случай закона больших чисел, имеющего большое значение в теории вероятностей и ее приложениях к статистике; построил математическую модель для описания серии независимых испытаний (схема Бернулли). Благодаря его работам теория вероятностей приобрела важнейшее значение в практической деятельности.

родом из Антверпена, бежавших из города после захвата его

испанцами и поселившихся в 1622 году в Базеле.
По крайней мере восемь ее представителей оставили заметный след в истории точных наук.
Среди академиков Петербургской Академии наук — пятеро представителей семьи Бернулли.
Примечательно не то, что это семейство сделало ряд значимых открытий в разных областях науки, а то, что они, за исключением только некоторых членов семьи, были как-либо связаны с наукой, в частности с математикой

I (1667-1748)
Николай II (1695-1726)
Даниил

I (1700-1782)

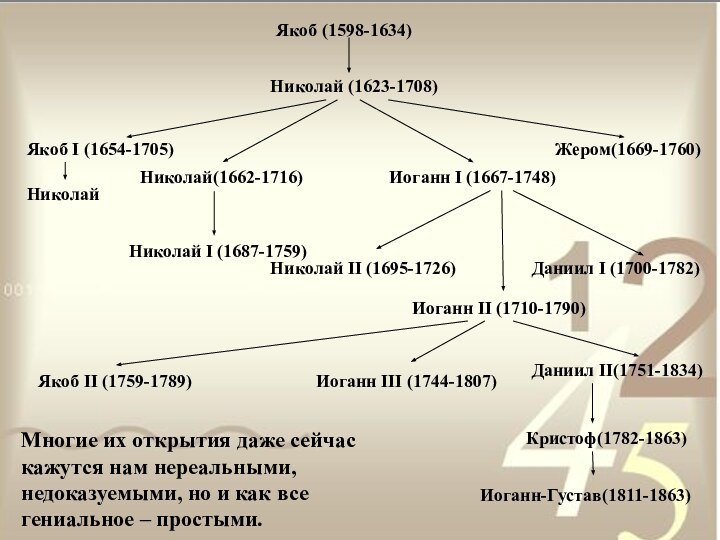
Иоганн II (1710-1790)

Якоб II (1759-1789)

Иоганн III (1744-1807)

Даниил II(1751-1834)

Кристоф(1782-1863)

Иоганн-Густав(1811-1863)

Многие их открытия даже сейчас кажутся нам нереальными, недоказуемыми, но и как все гениальное – простыми.

как результат счета различных предметов: людей, животных, птиц, деревьев,

орудий труда и т.д. Ряд натуральных чисел:
1, 2, 3, 4, 5, …

является бесконечным и называется натуральным рядом.
При изучении свойств чисел Я. Бернулли встретился с суммированием степеней натуральных чисел
Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, указал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы для сумм от S( Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, указал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы для сумм от S(n Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, указал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы для сумм от S(n) до S( Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, указал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы для сумм от S(n) до S(n Эти вопросы интересовали математиков и ранее. Я. Бернулли составил таблицу фигурных чисел, указал их свойства и на основании отмеченных свойств нашел формулы для сумм степеней натуральных чисел. Он привел формулы для сумм от S(n) до S(n10):

Запись чисел.

+33+…n3
. . . . . . .

. .
Sk (n)=1k +2k +3k+…nk

S10(1000)=110+210+310+…100010

Обозначим эти суммы следующим символом: S.
2) Возведем числа (от

первого числа до числа n) этих сумм в степень.
3) С помощью разложения:

Которое мы получили при последовательном возведении двучлена (бинома) a+b первую, вторую, третью, … степени
a+b=1·a+1·b
(a+b)2=1·a2+2·ab+1·b2
(a+b)3=1·a3+3·a2b+3·ab2+1·b3
(a+b)4=1·a4+4·a3b+6·a2b2+4·ab3+1·b4
напишем тождество:

числа до числа n.
5) Складываем результаты слева и справа

и получаем:

6) Вместо Sk(n) подставим числа

Отсюда вытекает рекуррентное соотношение:

S1(n), S2(n),…Sk-1(n)
Например, проверим, что
Находя
Находя
и так далее…

,B2 ,... найденная Я. Бернулли в связи с вычислением

суммы одинаковых степеней натуральных чисел.
Из формулы S1 (n), S2 (n), S3(n) следует что,

В0=1, B1= , B2= , B3=0
Из определения и рекуррентного соотношения вытекает простой способ вычисления чисел Бернулли. Из следующей формулы мы можем вычислить Bk

четырех чисел Бернулли. Я проверю значение B4



Для расчета

B4 нам также понадобились следующие значения

Sk(n) вычисляются с помощью чисел Вk.

Коэффициент при n2 оказывается

равным ,

коэффициент при n3 равен ,наконец,

коэффициент при степени nk оказывается не зависящим от k и всегда равным


Таким образом, формула Бернулли имеет вид

+25 +35 +…+n5

За счет этой формулы мы с легкостью

можем высчитать сумму степеней любого числа, например;