площині ГМТ визначається так:
Геометричним місцем точок називається фігура, що
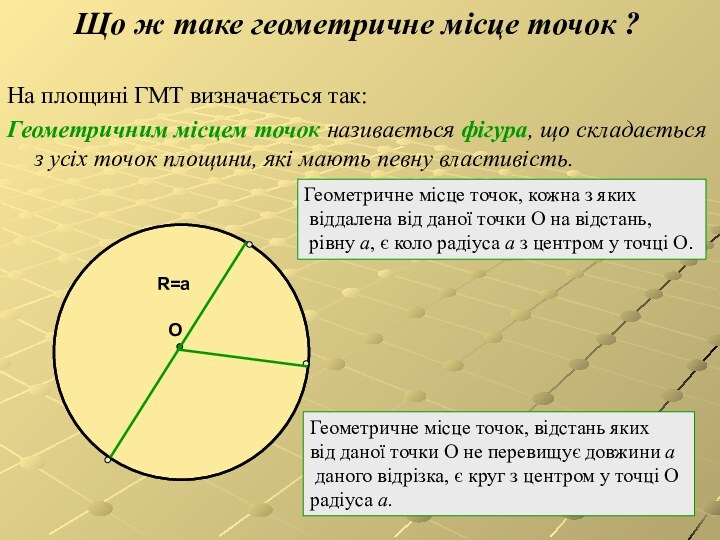
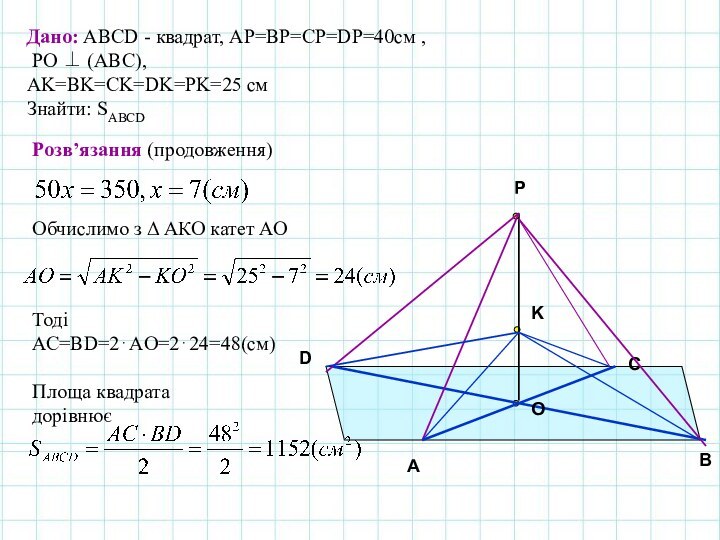
складається з усіх точок площини, які мають певну властивість.Геометричне місце точок, кожна з яких
віддалена від даної точки О на відстань,
рівну a, є коло радіуса a з центром у точці О.
Геометричне місце точок, відстань яких
від даної точки О не перевищує довжини a
даного відрізка, є круг з центром у точці О
радіуса a.
О
R=a