Презентация на тему Численное интегрирование

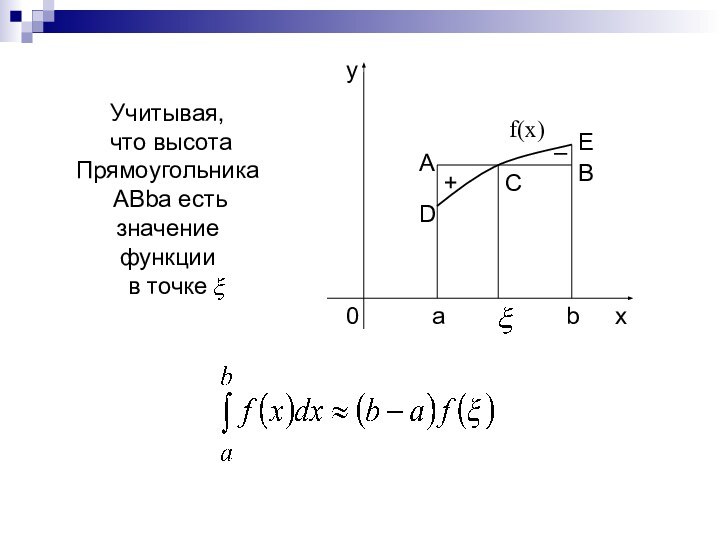
то определенный интеграл
от этой функции

подынтегральная функция
на отрезке задана таблично.

Формулы
приближенного интегрирования
называются

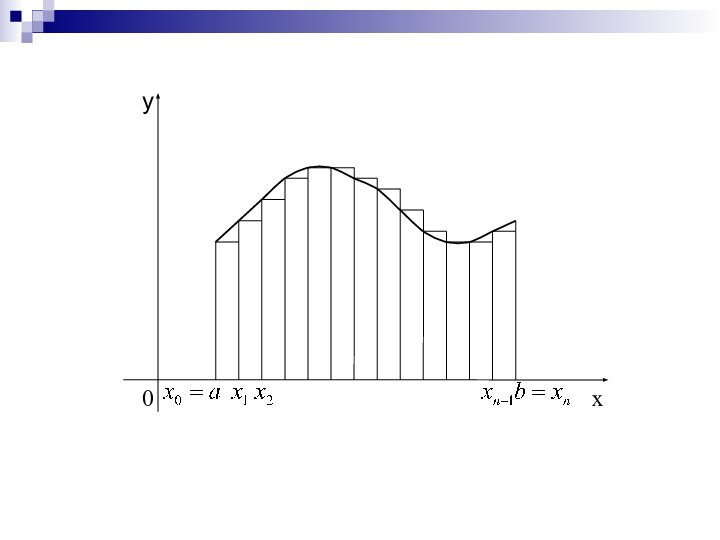
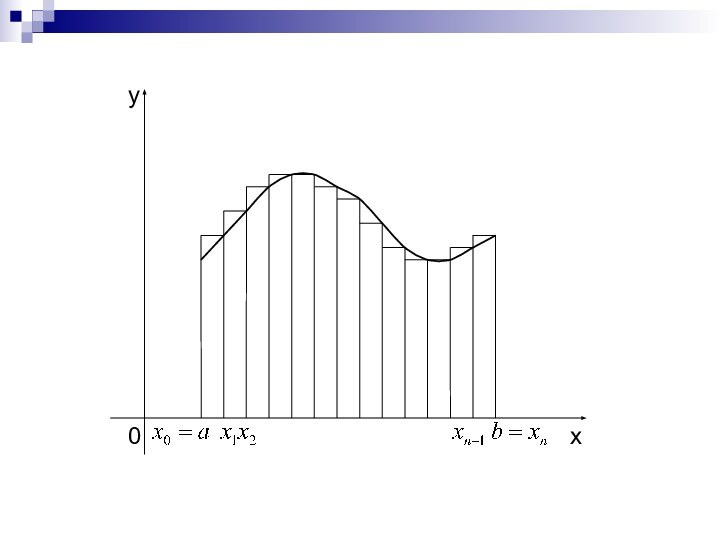
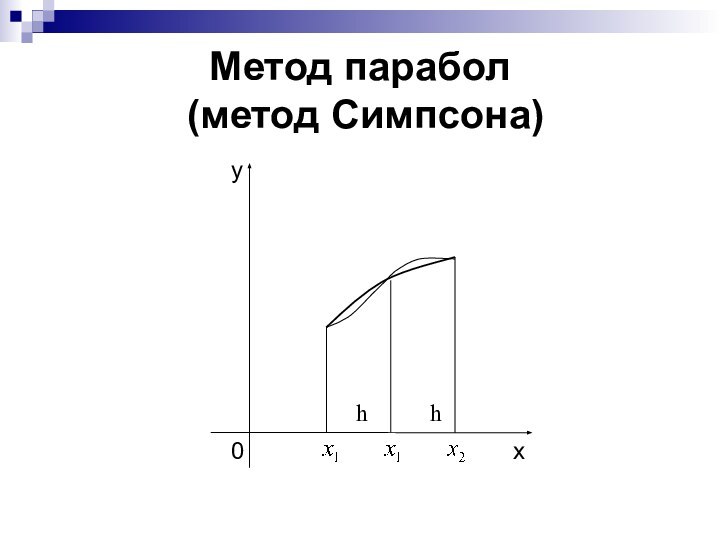
Задача численного интегрирования

интегральная сумма, соответствующая
некоторому разбиению отрезка

и некоторому выбору точек

,

,…,

на отрезках разбиения

площади
криволинейной трапеции,
ограниченной функцией f(x),
осью абсцисс и

в точке
f(x)
–

разбить на несколько частей
и для

(i = 0, 1, …,n – 1),
а высотой число

т.е. значение функции
в точке

равные части, а точки
 (i = 0, 1, …, n – 1) совмещать с левыми

концами отрезков разбиения.

то приближенное значение
интеграла может быть
представлено
формулой левых

где

– шаг.

конец отрезка
то приближенное значение
интеграла вычисляется
по формуле

.

подынтегральной функции y = f(x)
стягивающей ее хордой и
вычислим площадь

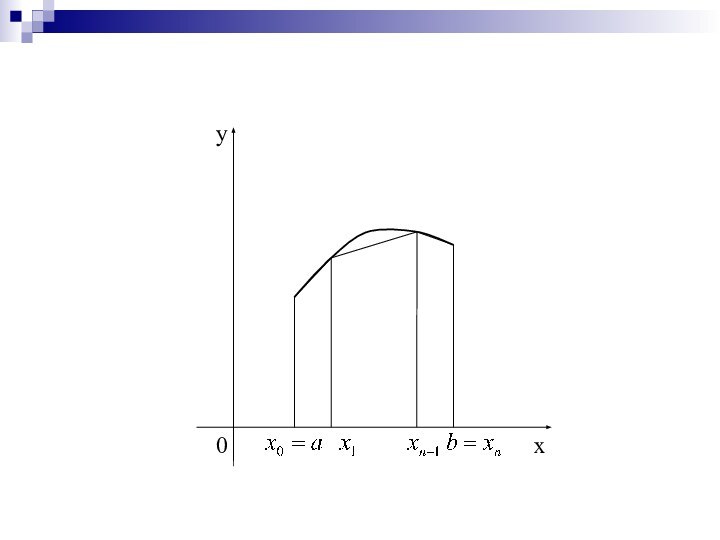
Это и есть формула трапеций

применить
формулу трапеции
к каждому отрезку
Тогда

на равные части,
в этом случае длина

Численное значение
интеграла на отрезке

равно

общей формулой трапеции.
Ее можно переписать в виде

где

– шаг.

принимающей в узлах
,
,
значения
,
и

В качестве интерполяционного
многочлена воспользуемся
многочленом Ньютона

n пар участков
и заменяя подынтегральную
функцию интерполяционным