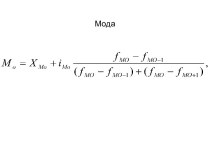FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
Сумма углов четырехугольника АОВС равна 360°. ∠С известен, ∠ОАС = ∠ОВС = 90°, т.к. радиусы, проведенные в точки касания, перпендикулярны касательным.
Тогда ∠АОВ = 360° - 68° - 90° - 90° = 112°.
Треугольник АОВ - равнобедренный, значит углы при основании ∠ВАО= ∠АВО.
∠АВО = (180° - 112°) : 2 = 34°. Ответ: 34
1
2
На окружности с центром О отмечены точки А и В так, что ∠АОВ = 140°. Длина меньшей дуги АВ равна 98. Найдите длину большей дуги АВ.
∠AOD = ∠ВОС = 108° - вертикальные.
Треугольник ВОС - равнобедренный, т.к. ВО = ОС (радиусы). В равнобедренном треугольнике углы при основании равны, значит ∠ОВС = ∠ВСО. Сумма углов в треугольнике 180°. ∠ВСО = (180° - 108°) : 2 = 36°. А угол ВСО это и есть угол АСВ, который надо найти.
Ответ: 36
3
Угол ABD - вписанный и опирается на дугу AD, значит дуга AD в 2 раза больше этого угла и равна 32°.
Угол CAD - вписанный и опирается на дугу CD, значит дуга CD в 2 раза больше этого угла и равна 64°.
Угол АВС также вписанный и опирается на дугу АС. А дуга АС состоит из дуг AD и АС и равна 32° + 64° = 96°.
Теперь найдем угол АВС: 96° : 2 = 48°.
Ответ: 48
4
Если сторона АС проходит через точку О, то АС - диаметр. Угол, опирающийся на диаметр - прямой, т.е. ∠АВС = 90°. Сумма острых углов в прямоугольном треугольнике равна 90°
∠С = 90° - ∠А = 90° - 74° = 16°.
Ответ: 16
5
