- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Движения
Содержание
- 2. Движение – это отображение плоскости на себя, сохраняющее расстояние между точками.
- 3. Виды движенияЦентральная симметрияОсевая симметрияПараллельный переносПоворот
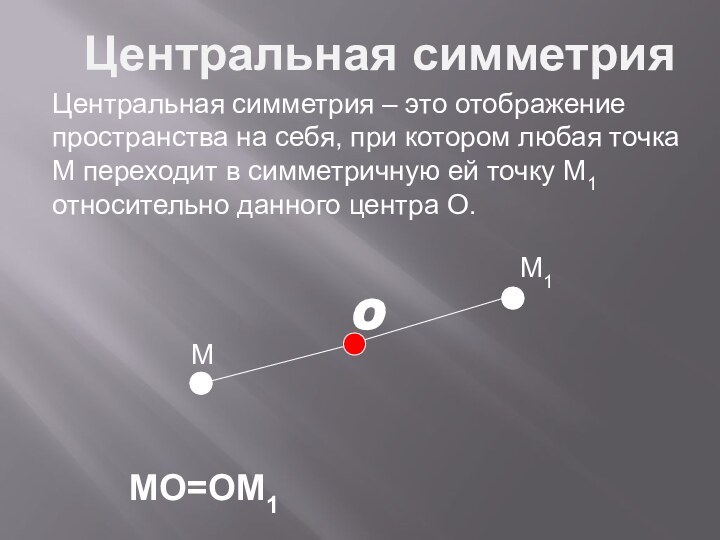
- 4. MM1MO=OM1OЦентральная симметрия Центральная
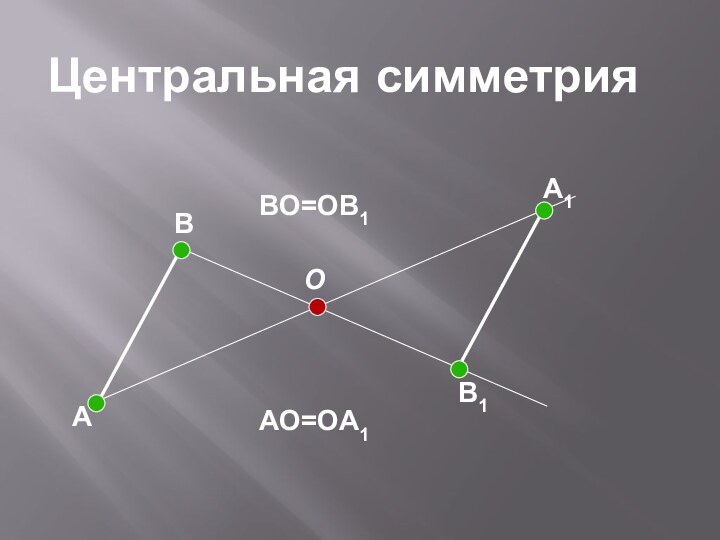
- 5. ABOB1A1Центральная симметрияBO=OB1AO=OA1
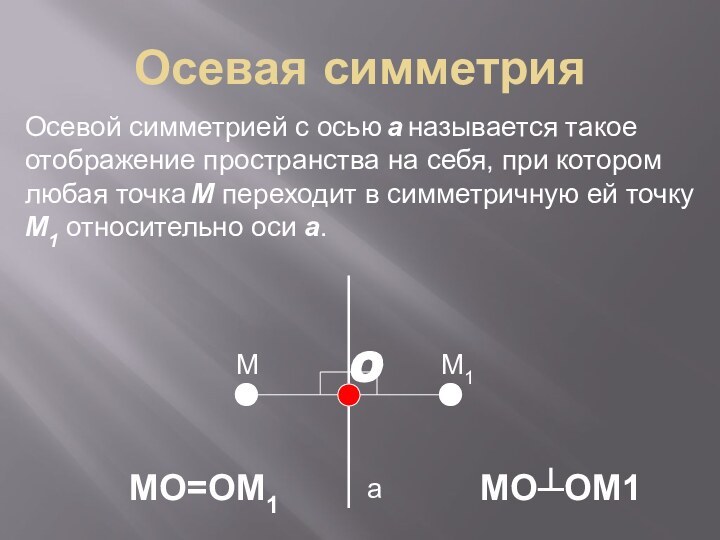
- 6. Осевая симметрия аMM1Осевой
- 7. Параллельный переносПараллельным переносом на вектор называется отображение
- 8. ПоворотЭто такое преобразование плоскости, прикотором точка О
- 9. Симметрия в жизни
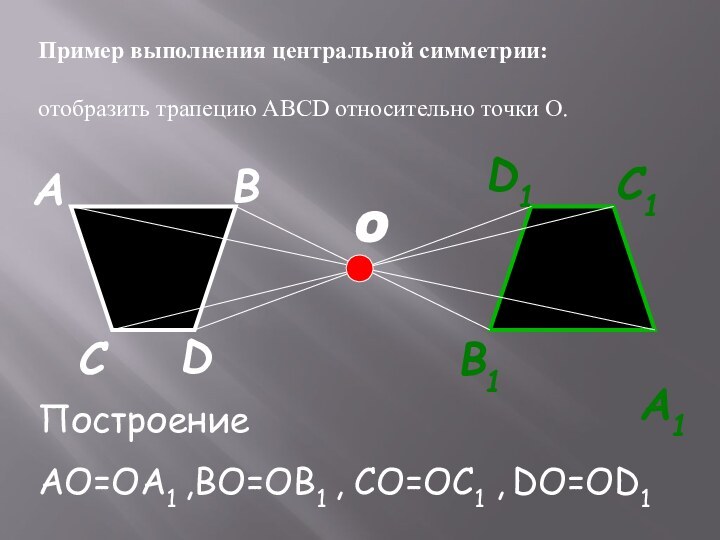
- 10. O АBА1DD1C1B1CПример выполнения центральной симметрии: отобразить
- 11. Скачать презентацию
- 12. Похожие презентации
Движение – это отображение плоскости на себя, сохраняющее расстояние между точками.






Слайд 4
M
M1
MO=OM1
O
Центральная симметрия
Центральная
симметрия – это отображение пространства на себя, при котором
любая точка М переходит в симметричную ей точку М1 относительно данного центра О.
Слайд 6
Осевая симметрия
а
M
M1
Осевой
симметрией с осью а называется такое отображение пространства на
себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а.O
MO=OM1
MO┴OM1
Слайд 7
Параллельный перенос
Параллельным переносом на вектор называется отображение пространства
на себя, при котором
ММ1=
M
M1
║
ММ1
Слайд 8
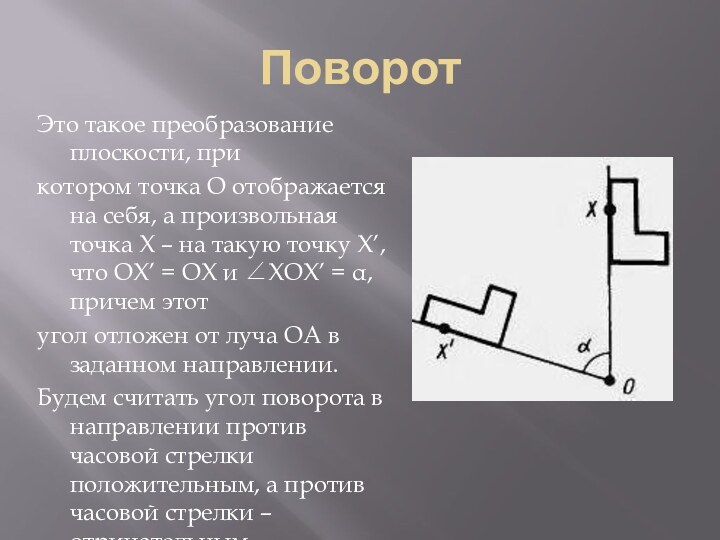
Поворот
Это такое преобразование плоскости, при
котором точка О отображается
на себя, а произвольная точка Х – на такую
точку Х’, что ОХ’ = ОХ и ∠ХОХ’ = α, причем этотугол отложен от луча ОА в заданном направлении.
Будем считать угол поворота в направлении против часовой стрелки положительным, а против часовой стрелки – отрицательным.