- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Фалес Милетский 10 класс
Содержание
- 2. СодержаниеКраткая биографияКарта Древней ГрецииАфоризмы ФалесаТеорема ФалесаИстория открытия некоторых теоремФилософия ФалесаКосмология ФалесаМатематика и астрономияФалесМилетский ТеатрСписок литературы
- 3. Краткая биография ФАЛЕС (Thales) (ок.
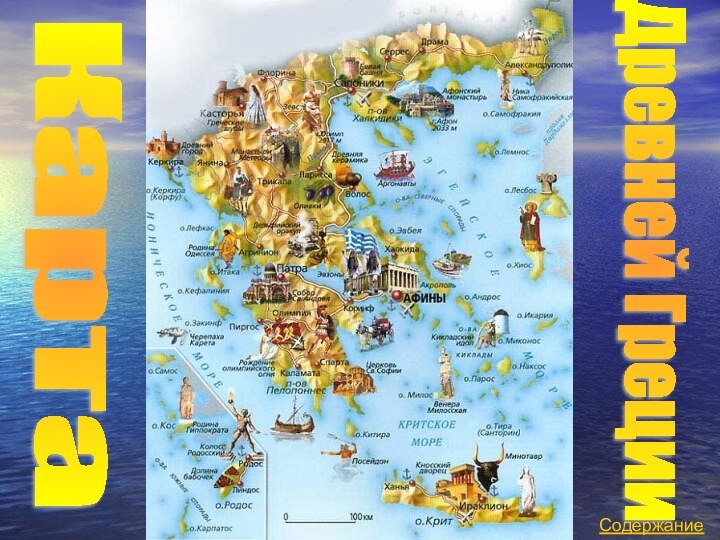
- 4. КартаДревней ГрецииСодержание
- 5. Афоризмы ФалесаЧто прекраснее всего? - Мир, ибо
- 6. Теорема ФалесаТеорема: Если параллельные прямые, пересекающие стороны
- 7. История открытия некоторых теорем Фалес
- 11. Философия Фалеса Первым в ряду
- 12. Космология Фалеса Аристотель сопоставляет с
- 13. Математика и астрономия В свое
- 14. Важнейшей заслугой Фалеса в
- 15. ФалесСодержание
- 16. Милетский театрСодержание
- 17. Список использованной литературыЛебедев «Фрагменты ранних греческих философов»
- 18. Конец
- 19. Скачать презентацию
- 20. Похожие презентации


















Слайд 2
Содержание
Краткая биография
Карта Древней Греции
Афоризмы Фалеса
Теорема Фалеса
История открытия некоторых
теорем
Слайд 3
Краткая биография
ФАЛЕС (Thales) (ок. 640
— ок. 546), древнегреческий философ и ученый, основатель так
называемой ионийской (милетской) школы, родоначальник античной философии и науки; в древности почитался как один из «Семи мудрецов». Аристотель начинает с Фалеса историю метафизики, Евдем — историю астрономии и геометрии.Происходил из города Милета в Малой Азии, принадлежа к аристократическому роду. Был близок милетскому тирану Фрасибулу и связан с храмом Аполлона Дидимского, покровителя морской колонизации. По свидетельству Диогена Лаэртского, бывал в Египте и жил у жрецов, изучая астрономию и геометрию. Видимо, Фалес использовал достижения древневосточной науки египтян, вавилонян и финикийцев. Диоген Лаэртский сообщает, что Фалес установил продолжительность года и разделил его на 365 дней. По словам Геродота, в 585 до н. э. мудрец предсказал полное солнечное затмение.
По свидетельству Прокла, Фалес первый стал доказывать геометрические теоремы; ему принадлежат доказательства следующих положений: 1) круг делится диаметром пополам; 2) в равнобедренном треугольнике углы при основании равны; 3) при пересечении двух прямых образуемые ими вертикальные углы равны; 4) два треугольника равны, если два угла и сторона одного из них равны двум углам и соответствующей стороне другого.
Содержание
Слайд 5
Афоризмы Фалеса
Что прекраснее всего? - Мир, ибо он
творение бога. Что быстрее всего? - Быстрее всего ум,
он обегает все. Что всего мудрее? - Время, ибо оно одно открывает всё. Что самое общее для всех? - Надежда, ибо если у кого и ничего нет, то она есть. Что сильнее всего? - Необходимость, ибо она властвует над всем. Что трудно? - Познать самого себя. Что легко? - Давать советы другим. Кто счастлив? - Тот, кто здоров телом, одарен спокойствием духа и развивает свои дарования. Как легче всего переносить несчастье? - Если видеть врагов своих в еще худшем положении. Невежество - тяжкое бремя. Поучай и учись лучшему. Те, кто совершают грех, не могут спрятаться от божьего ока и даже не могут утаить от него свои мысли. Я благодарен судьбе за три вещи: во-первых, за то, что родился человеком, а не зверем; во-вторых, за то, что мужчиной, а не женщиной; в-третьих, что эллином, а не варваром. Поручись и пострадаешь. "Чем отличается жизнь от смерти?" - спросили Фалеса. - "Ничем". "Почему же ты тогда не умираешь?" - "Потому, - ответил он, - что нет никакой разницы".Содержание
Слайд 6
Теорема Фалеса
Теорема: Если параллельные прямые, пересекающие стороны угла,
отсекают на одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне.Доказательство:
Пусть А1, А2, А3 - точки пересечения параллельных прямых с одной из сторон угла и А2 лежит между А1, А3.
Пусть В1, В2, В3-соответствующие точки пересечения этих прямых с другой стороной угла.
Докажем, что если А1А2=А2А3, то В1В2=В2В3.
Проведем через точку В2 прямую С1С2, параллельную прямой А1А3. По свойству параллелограмма А1А2=С1В2, А2А3=В2С2. И так как А1А2=А2А3, то С1В2=В2С2.
Треугольники В2В1С1 и В2В3С2 равны по второму признаку. У них С1В2=В2С2 по доказанному. Углы при вершине В2 равны как вертикальные, а углы В2С1B1и В2С2B3 равны как внутренние накрест лежащие при параллельных А1B1 и А3B3 и секущей С1С2.
Из равенства треугольников следует равенство сторон: B1B2=B2B3.
Теорема доказана.
Замечание:
В условиях теоремы Фалеса вместо сторон угла можно взять любые две прямые, при этом заключене теоремы будет то же:
Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекают равные отрезки и на другой прямой.
Содержание
Слайд 7
История открытия некоторых теорем
Фалес открыл
любопытный способ определения расстояния от берега до видимого корабля.
Одни историки утверждают, что для этого им был использован признак подобия прямоугольных треугольников. Другие историки (Прокл) говорят, что Фалес применил признак конгруэнтности прямоугольных треугольников, то есть точку D он выбирал так, чтобы наблюдатель D, корабль B и середина отрезка AC, то есть точка E, лежали на одной прямой. Тогда |AB|=|CD|.
Столь же остроумно предложил Фалес измерять высоту предметов. Став недалеко от предмета, надо дождаться, пока тень от человека не сделается равной его росту. Измерив тогда длину тени предмета, можно заключить, что она равна высоте предмета. Говорят, что таким способом Фалес измерял высоту египетских пирамид.
Проиллюстрируем этот пример на чертеже. Пусть A - точка берега, B - корабль. На берегу восстанавливается перпендикуляр AC произвольной длинны. Из точки C проводится перпендикуляр CD в противоположную от моря сторону. Из точки D смотрят на корабль и фиксируют на [AC] точку E - точку пересечения [AC] c [DB]. Тогда длинна отрезка AB во столько раз больше (или меньше) длинны отрезка CD, во сколько раз |AC| больше(или меньше) |CE|.
Содержание
Слайд 11
Философия Фалеса
Первым в ряду милетских
философов был Фалес. Он происходил из знатного финикийского рода,
был современником Солона и Креза.Несмотря на огромное значение, которое он имеет, о нем мало известно.
Будучи купцом, он использовал торговые поездки в целях расширения научных сведений и знания, которые он приобрел в Финикии и Египте – перенес в Грецию
Он был гидроинженером, прославившимся своими работами, разносторонним учёным и мыслителем, изобретателем астрономических приборов. Как учёный он широко прославился в Греции, сделав удачное предсказание солнечного затмения, наблюдавшегося в Греции в 585 г. до н.э. Для этого предсказания Фалес использовал почерпнутые им в Египте астрономические сведения, восходящие к наблюдениям и обобщениям вавилонской науки.
Содержание
Слайд 12
Космология Фалеса
Аристотель сопоставляет с мифологическими
учениями ГомераАристотель сопоставляет с мифологическими учениями Гомера и ГесиодаАристотель
сопоставляет с мифологическими учениями Гомера и Гесиода. Космология Фалеса весьма напоминает египетское учение. ВселеннаяАристотель сопоставляет с мифологическими учениями Гомера и Гесиода. Космология Фалеса весьма напоминает египетское учение. Вселенная, по представлению Фалеса, представляет жидкую массу, посередине которой находится воздушное тело, имеющее форму чаши, повёрнутой открытой стороной вниз. Вогнутая поверхность этой чаши — небо; на нижней поверхности, в центре её, плавает диск, обтекаемый водой. Звёзды — боги, плавающие по небесному своду. С космологическими представлениями связаны и философские воззрения Фалеса. Фалеса интересовали два тесно связанных между собой вопроса, а именно: из чего всё произошло и что составляет принцип и сущность всего (архэАристотель сопоставляет с мифологическими учениями Гомера и Гесиода. Космология Фалеса весьма напоминает египетское учение. Вселенная, по представлению Фалеса, представляет жидкую массу, посередине которой находится воздушное тело, имеющее форму чаши, повёрнутой открытой стороной вниз. Вогнутая поверхность этой чаши — небо; на нижней поверхности, в центре её, плавает диск, обтекаемый водой. Звёзды — боги, плавающие по небесному своду. С космологическими представлениями связаны и философские воззрения Фалеса. Фалеса интересовали два тесно связанных между собой вопроса, а именно: из чего всё произошло и что составляет принцип и сущность всего (архэ, др.-греч. ἀρχή). Фалес отвечал на эти вопросы следующим образом: вода есть сущность всего, из воды всё произошло и в воду все вновь возвращается. В пользу этого мнения Фалес приводил три довода: во-первых, семя всех живых существ есть нечто обладающее влажностью; во-вторых, все растения питаются влагой и благодаря ей приносят плоды, лишённые же влаги растения засыхают; в-третьих, даже огонь солнца и светил питается испарениями воды.Содержание
Слайд 13
Математика и астрономия
В свое время
Фалес был едва ли не единственным во всей Древней
Греции человеком, отдавшимся чистой науке и абстрактному мышлению без преследования каких-нибудь практических целей. Его жизнь в Милете, посвящённая исключительно изучению природы и занятиям астрономией, не могла возбуждать уважения в торгашах, привыкших думать, что умный человек должен отдавать свой труд и время только занятиям, приносящим барыши. Известен, например, анекдот о жестоких насмешках, которым он подвергся со стороны одной женщины за то, что, смотря на небо, не увидел на земле камня, о который и споткнулся.Два случая не только подняли Фалеса во мнении его сограждан, но и заставили их, как и других греков, признать его первым мудрецом во всей Греции. Сведения о первом случае сообщает Аристотель. Однажды уже с самого начала весны Фалес предвидел, что предстоит богатый сбор маслин Два случая не только подняли Фалеса во мнении его сограждан, но и заставили их, как и других греков, признать его первым мудрецом во всей Греции. Сведения о первом случае сообщает Аристотель. Однажды уже с самого начала весны Фалес предвидел, что предстоит богатый сбор маслин. С целью доказать своим согражданам, что и из его занятий могут быть извлечены денежные выгоды, он заблаговременно скупил по низкой цене как в Милете Два случая не только подняли Фалеса во мнении его сограждан, но и заставили их, как и других греков, признать его первым мудрецом во всей Греции. Сведения о первом случае сообщает Аристотель. Однажды уже с самого начала весны Фалес предвидел, что предстоит богатый сбор маслин. С целью доказать своим согражданам, что и из его занятий могут быть извлечены денежные выгоды, он заблаговременно скупил по низкой цене как в Милете, так и в Хиосе Два случая не только подняли Фалеса во мнении его сограждан, но и заставили их, как и других греков, признать его первым мудрецом во всей Греции. Сведения о первом случае сообщает Аристотель. Однажды уже с самого начала весны Фалес предвидел, что предстоит богатый сбор маслин. С целью доказать своим согражданам, что и из его занятий могут быть извлечены денежные выгоды, он заблаговременно скупил по низкой цене как в Милете, так и в Хиосе, все свободные прессы для выделки масла. Когда его предвидение оправдалось и вследствие громадного урожая маслин потребовалось большое количество прессов, он продал их по очень высокой цене и таким образом получил значительную выгоду. Вторым случаем, распространившим славу Фалеса на всю Грецию, было сделанное им всенародно в Милете предсказание о предстоявшем в 585 г. Два случая не только подняли Фалеса во мнении его сограждан, но и заставили их, как и других греков, признать его первым мудрецом во всей Греции. Сведения о первом случае сообщает Аристотель. Однажды уже с самого начала весны Фалес предвидел, что предстоит богатый сбор маслин. С целью доказать своим согражданам, что и из его занятий могут быть извлечены денежные выгоды, он заблаговременно скупил по низкой цене как в Милете, так и в Хиосе, все свободные прессы для выделки масла. Когда его предвидение оправдалось и вследствие громадного урожая маслин потребовалось большое количество прессов, он продал их по очень высокой цене и таким образом получил значительную выгоду. Вторым случаем, распространившим славу Фалеса на всю Грецию, было сделанное им всенародно в Милете предсказание о предстоявшем в 585 г. (28 мая) полном солнечном затмении, граница которого, как показывают новейшие астрономические вычисления, только несколькими милями проходила севернее Милета. После этого Фалес приобрёл заметное влияние и на политическую жизнь своего родного города.
Содержание
Слайд 14 Важнейшей заслугой Фалеса в области
математики должно быть считаемо перенесение им из Египта в
Грецию первых начал теоретической элементарной геометрииВажнейшей заслугой Фалеса в области математики должно быть считаемо перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии. ЭвдемВажнейшей заслугой Фалеса в области математики должно быть считаемо перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии. Эвдем, по свидетельству Прокла, приписывает Фалесу открытие следующих геометрических предложений:Вертикальные углы равны.
Углы при основании равнобедренного треугольника равны.
Треугольник определяется стороной и прилежащими к ней двумя углами.
Диаметр делит круг на две равные части.
Содержание
Слайд 17
Список использованной литературы
Лебедев «Фрагменты ранних греческих философов» М.1989
г.
Бретшнайдер «Полное собрание сохранившихся сведений о Фалесе как математике
и астрономе» 1870г.О. Нейгебауер «Лекции по истории античных математических наук» 1937г.
Б.Л. Ван-дер-Варден «Пробуждающаяся наука II. Рождение астрономии» М.: Наука, 1991г.
Содержание