- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
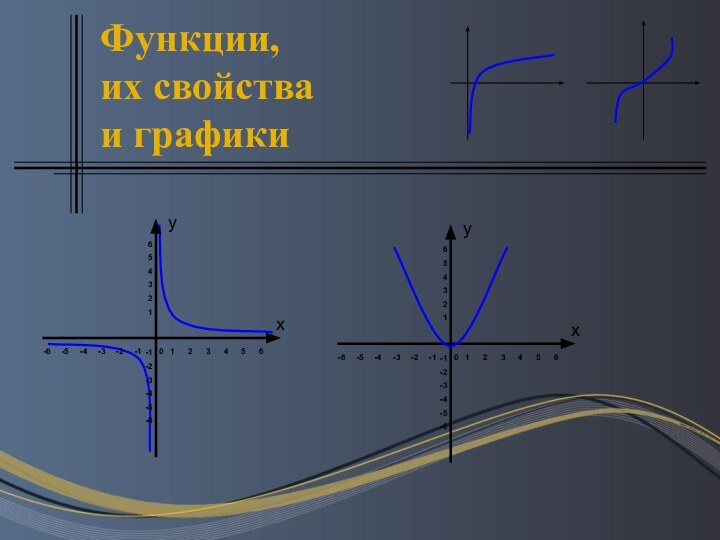
Презентация на тему Функции, их свойства и графики
Содержание
- 2. Функции, их свойства и графики
- 3. Темы:Функция.Использования функций в физике.Свойства функций.Квадратичная функция.Преобразование графиков функций.
- 4. Свойства функцийВозрастание и убывание функций.Свойства монотонных функций.Четные и нечетные функции.Ограниченные и неограниченные функции.
- 5. ФункцияФункция — математическое понятие, отражающее связь между
- 6. xYФункция
- 7. Использования функций в физикеПример:Волновая функция, или пси-функция
- 8. Квадратичная функция ОПРЕДЕЛЕНИЕ: Функцию которую можно задать формулой вида y=ax2+bx+c, где а0 называют квадратичной. У=х2
- 9. Квадратичная функцияПри а1 (a0), b=c=0, квадратичная функция
- 10. Квадратичная функцияПри а1 (a0), b=c=0, квадратичная функция
- 11. Построение y=ax2+bx+cm=-b/2a
- 12. Преобразование графиков функцийРастяжение и сжатие графиков функций к оси ординат.Графики функций y=|f(x)| и y=f(|x|).
- 13. Возрастание и убывание функцийФункция f называется возрастающей
- 14. Свойства монотонных функцийМонотонная функция каждое свое значение
- 15. Четные и нечетные функции ОПРЕДЕЛЕНИЕ:
- 16. Ограниченные и неограниченные функции ОПРЕДЕЛЕНИЕ: Функция
- 17. Ограниченные и неограниченные функцииФункция f ограничена снизу,
- 18. Растяжение и сжатие графиков функций к оси
- 19. График функций y=|f(x)|Построить y=|f(x)|Оставить без изменений ту
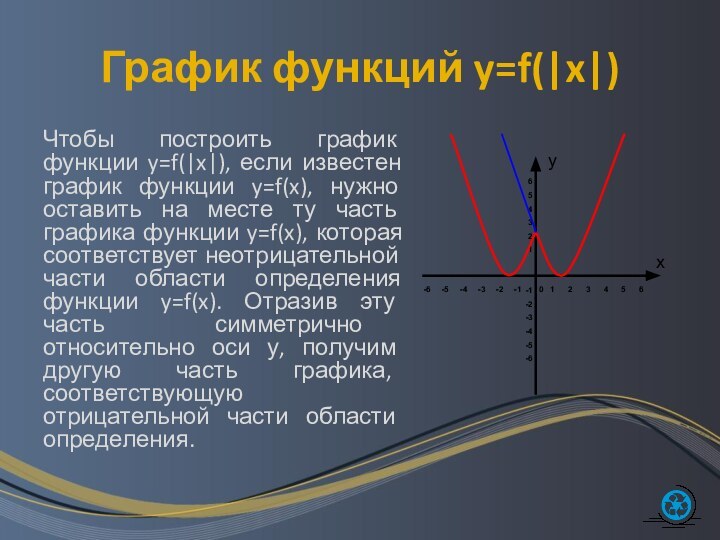
- 20. График функций y=f(|x|) Чтобы построить график функции
- 21. Скачать презентацию
- 22. Похожие презентации











Слайд 3
Темы:
Функция.
Использования функций в физике.
Свойства функций.
Квадратичная функция.
Преобразование графиков функций.
Слайд 4
Свойства функций
Возрастание и убывание функций.
Свойства монотонных функций.
Четные и
нечетные функции.
Слайд 5
Функция
Функция — математическое понятие, отражающее связь между элементами множеств.
Можно сказать, что функция это «закон», по которому каждому
элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений
Слайд 7
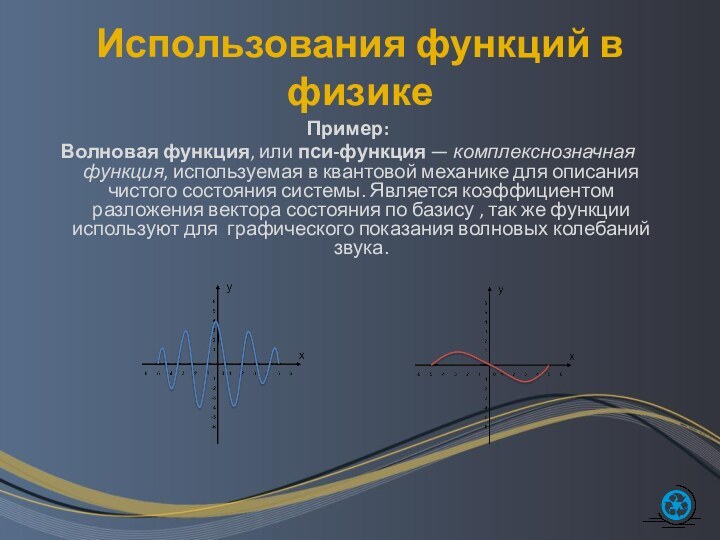
Использования функций в физике
Пример:
Волновая функция, или пси-функция —
комплекснозначная функция, используемая в квантовой механике для описания чистого
состояния системы. Является коэффициентом разложения вектора состояния по базису , так же функции используют для графического показания волновых колебаний звука.
Слайд 8
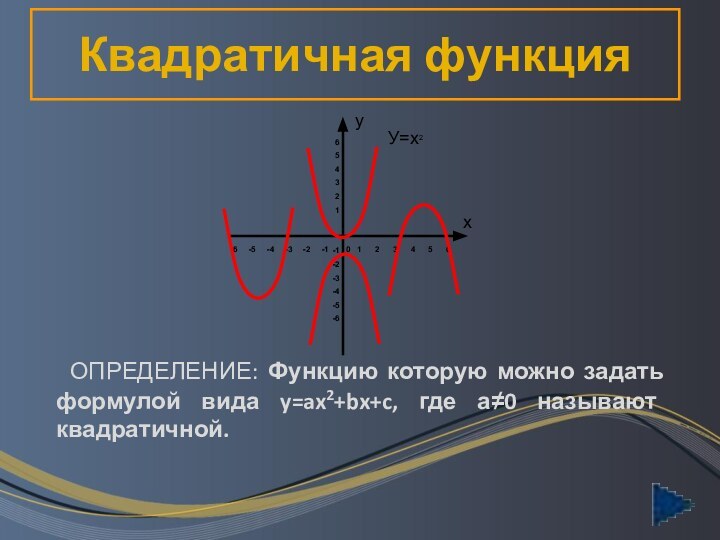
Квадратичная функция
ОПРЕДЕЛЕНИЕ: Функцию которую можно задать
формулой вида y=ax2+bx+c, где а0 называют квадратичной.
У=х2
Слайд 9
Квадратичная функция
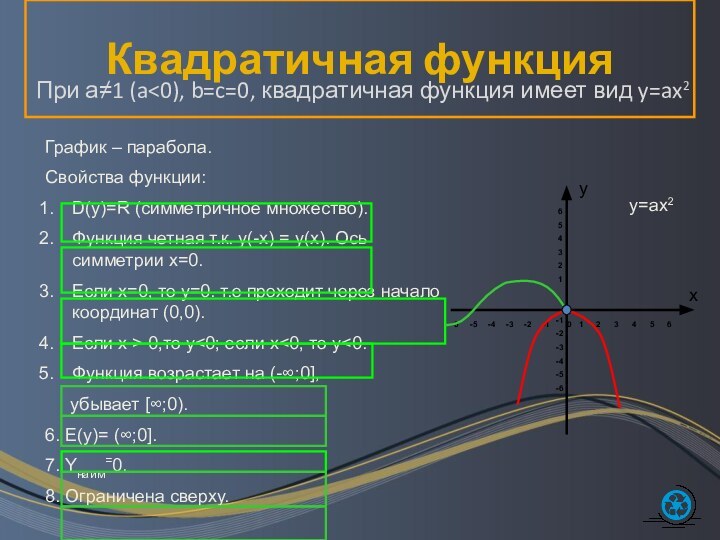
При а1 (a0), b=c=0, квадратичная функция имеет
вид y=ax2
График – парабола.
Свойства функции:
D(y)=R (симметричное множество).
Функция четная
т.к. y(-x) = y(x). Ось симметрии x=0.Если х=0, то у=0. т.е проходит через начало координат (0,0).
Если х > 0,то у>0; если x<0, то у>0.
Функция возрастает на [0; ∞),
убывает (- ∞;0].
6. E(y)= [0; ∞).
7. Yнаим=0.
8. Ограничена снизу.
х
у
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
y=ax2
Слайд 10
Квадратичная функция
При а1 (a0), b=c=0, квадратичная функция имеет
вид y=ax2
График – парабола.
Свойства функции:
D(y)=R (симметричное множество).
Функция четная
т.к. y(-x) = y(x). Ось симметрии x=0.Если х=0, то у=0. т.е проходит через начало координат (0,0).
Если х > 0,то у0; если x<0, то у0.
Функция возрастает на (-∞;0,
убывает [∞;0).
6. E(y)= (∞;0].
7. Yнаим=0.
8. Ограничена сверху.
х
у
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
y=ax2
Слайд 12
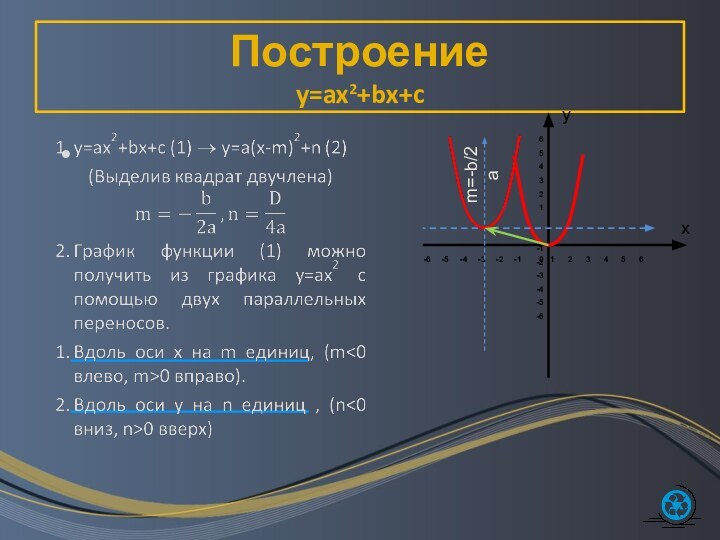
Преобразование графиков функций
Растяжение и сжатие графиков функций к
оси ординат.
Графики функций y=|f(x)| и y=f(|x|).
Слайд 13
Возрастание и убывание функций
Функция f называется возрастающей на
множестве Х, если для любых двух значений аргумента х1
и х2 множества Х, таких, что Х2>X1, выполняется неравенство f(x2)>f(x1)Функция f называется убывающей на множестве Х, если для любых двух значений аргумента х1 и х2 множества Х, таких, что Х2>X1, выполняется неравенство f(x2)
Слайд 14
Свойства монотонных функций
Монотонная функция каждое свое значение принимает
лишь при одном значении аргумента.
Если функция y=f(x) является возрастающей
(убывающей), то функция y=-f(x) является убывающей (возрастающей).Сумма двух возрастающих функций является возрастающей функцией, а сумма двух убывающих функций является убывающей функцией.
Если обе функции f и g возрастающие или обе убывающие, то функция ф(х)=f(g(x))- возрастающая функция.
Если функция y=f(x) монотонная на множестве Х и сохраняет на этом множестве знак, то функция g(x)=1:f(x) на множестве Х имеет противоположный характер монотонности.
Слайд 15
Четные и нечетные функции
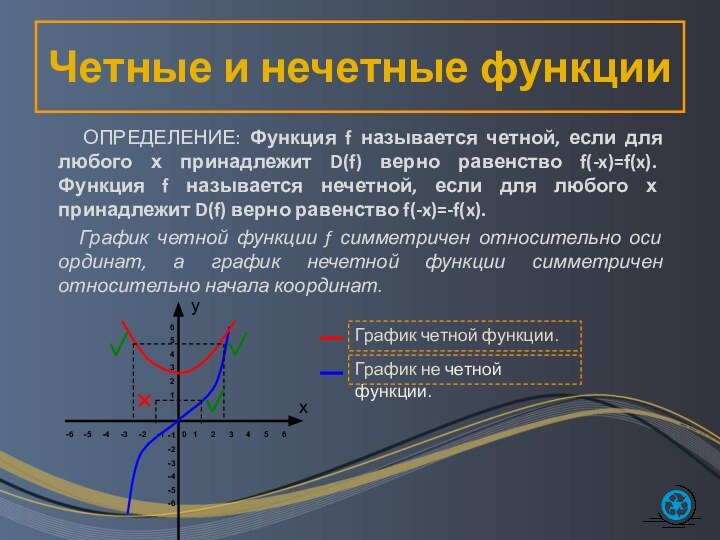
ОПРЕДЕЛЕНИЕ: Функция
f называется четной, если для любого х принадлежит D(f)
верно равенство f(-x)=f(x). Функция f называется нечетной, если для любого х принадлежит D(f) верно равенство f(-x)=-f(x).График четной функции f симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
График не четной функции.
График четной функции.
Слайд 16
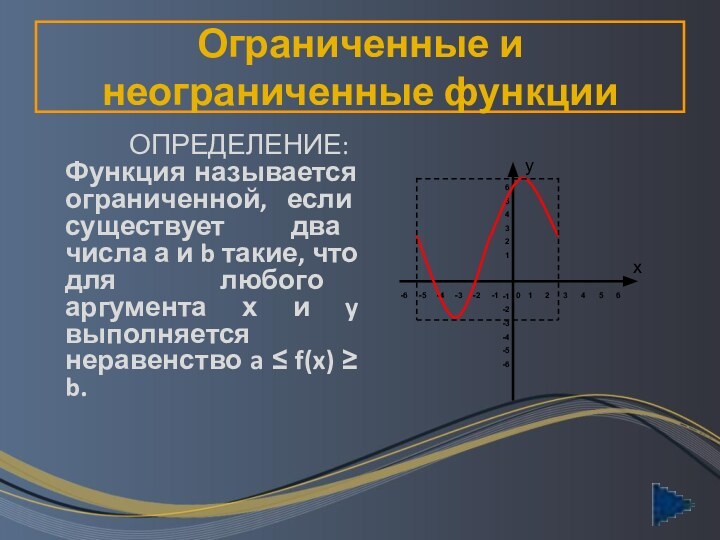
Ограниченные и неограниченные функции
ОПРЕДЕЛЕНИЕ: Функция называется
ограниченной, если существует два числа а и b такие,
что для любого аргумента х и y выполняется неравенство a f(x) b.
Слайд 17
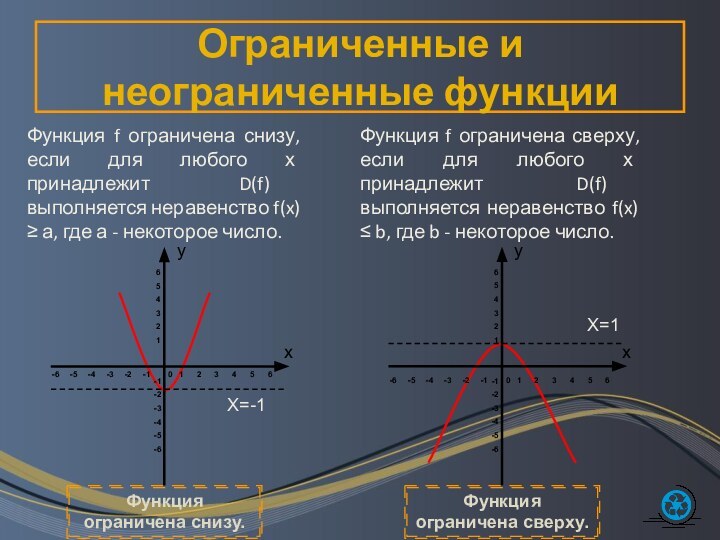
Ограниченные и неограниченные функции
Функция f ограничена снизу, если
для любого х принадлежит D(f) выполняется неравенство f(x)
а, где а - некоторое число.Функция f ограничена сверху, если для любого х принадлежит D(f) выполняется неравенство f(x) b, где b - некоторое число.
Функция ограничена снизу.
Функция ограничена сверху.
х
у
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
Х=1
Х=-1
Слайд 18
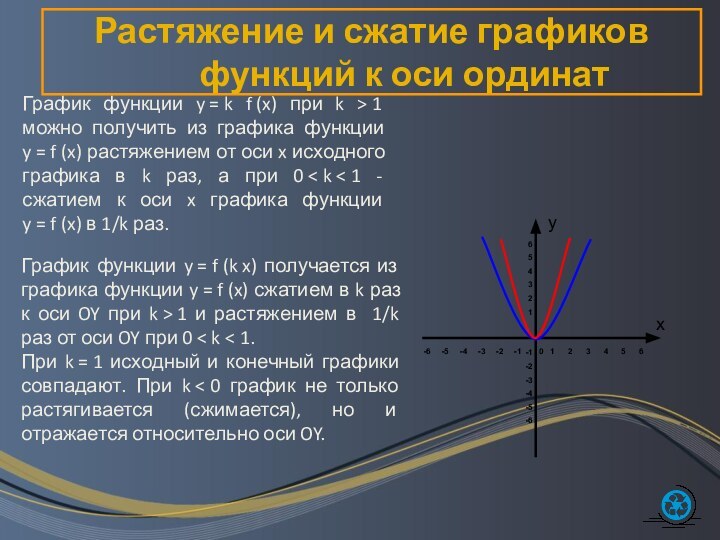
Растяжение и сжатие графиков функций к оси ординат
График
функции y = k f (x) при k > 1 можно получить из
графика функции y = f (x) растяжением от оси x исходного графика в k раз, а при 0 < k < 1 - сжатием к оси x графика функции y = f (x) в 1/k раз.График функции y = f (k x) получается из графика функции y = f (x) сжатием в k раз к оси OY при k > 1 и растяжением в 1/k раз от оси OY при 0 < k < 1.
При k = 1 исходный и конечный графики совпадают. При k < 0 график не только растягивается (сжимается), но и отражается относительно оси OY.