Презентация на тему Функция (9 класс)

с подготовкой к экзамену
Проблема – в школьном курсе алгебры

недостаточно задач с модулем
Объект исследования – функция
Предмет исследования – функция у=|x|
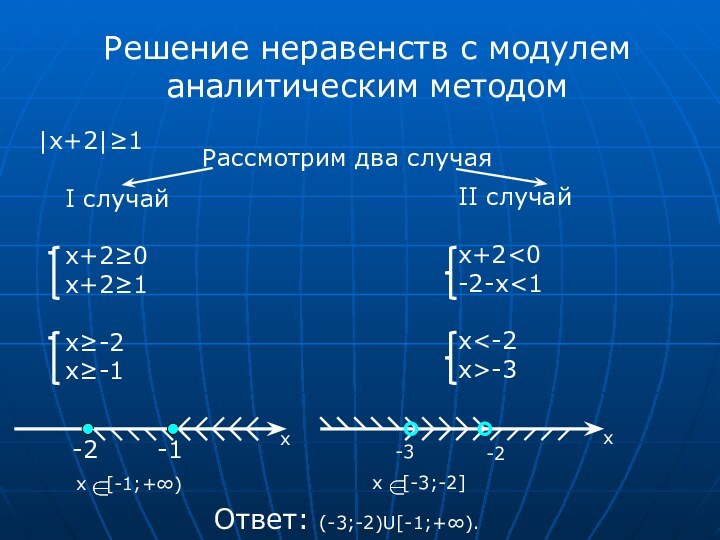
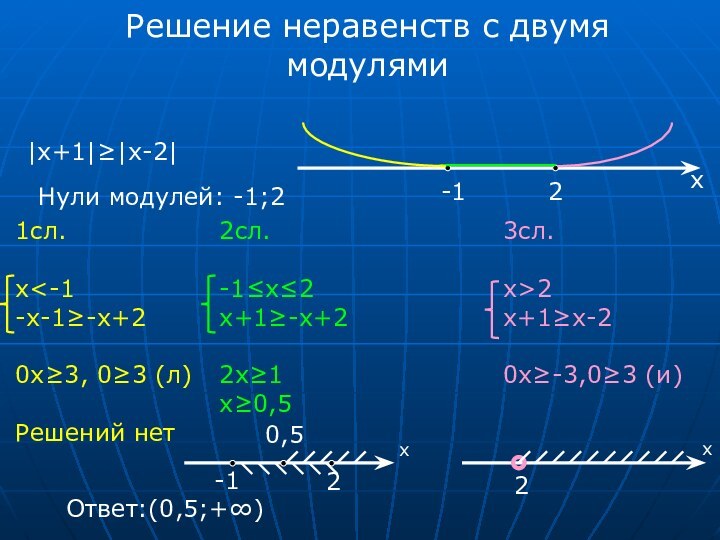
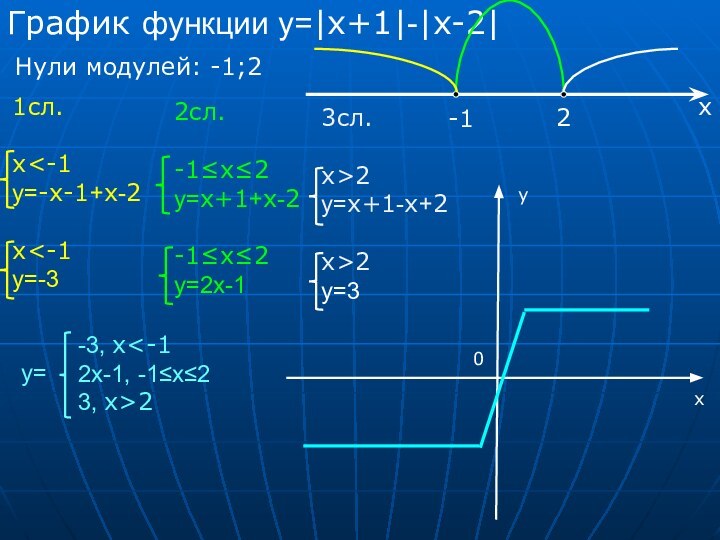
Цель – рассмотреть решение распространённых задач с модулем
Гипотеза – я предполагал, что задачи с модулем решаются только графически
Задачи –
1.Вспомнить известную мне информацию о задачах с модулем
2.Придумать новые задачи
3.Проконсультироваться с учителем
4.Создать презентацию
5.Защитить работу

или модуль числа х.
Абсолютная величина числа х равна этому

числу, если х>0, равна противоположному числу –х, если x<0, и равна нулю, если х=0.
Таким образом, функция |x| определена для всех
х (-∞;+∞).
Множество её значений совпадает с множеством неотрицательных чисел.

х, если х≥0,
-х, если х<0.

|x|=

функции

≥
y=|x|-2
y=

0
x
y

1

4

Ответ: [4;+∞)

3 случая

Iсл. c>1, 2 решения

IIсл. c

1 решение

|x+2|+1 =c

y=|x+2|+1

y=c

у

Сколько решений имеет уравнение

способ
Рассмотрим два случая
1 случай

x-3≥0
x-3=5

x=5+3
x=8, 8-3≥0 (и)

2 случай

x-3

-2-3<0 (и)

Ответ:-2, 8

II способ

x-3=5 или x-3=-5
x=8 x=-2

на координатной прямой.
Решить уравнение на каждом из промежутков с

помощью системы.
Написать ответ.

7

x>3
x=x-3+4-x

x=1 ,1>3 (л)

Решений нет

Ответ: 7/3.

случай

x+2≥0
x+2≥1

x≥-2
x≥-1

II случай

x+2

|x-2.5|>2.
Геометрически выражение |x-2.5| означает расстояние р(x-2.5)
на координатной прямой

между точками х и 2.5. Значит, нам нужно
Найти все такие точки х, которые удалены от точки 2.5 более, чем на 2-
это точки из промежутков (-∞;0.5) и (4.5;+∞)
Итак, получили следующее решения неравенства: х<0.5;x>4.5.

Четвёртый способ.
Поскольку обе части заданного неравенства неотрицательны,
то возведение их в квадрат есть равносильное преобразование
неравенства. Получим |2x-5|2>42
Воспользовавшись тем что |x|2=x2, получим
(2x-5-4)(2x-5+4)>0
Применив метод интервалов получим тот же ответ.

на координатной прямой.
Решить неравенство на каждом из промежутков с

помощью системы.
Написать ответ.

0≥3 (л)

Решений нет

2сл.

-1≤x≤2
х+1≥-x+2

2х≥1
х≥0,5
3сл.

x>2
х+1≥х-2

0x≥-3,0≥3 (и)





Ответ:(0,5;+∞)
-1
2
х
0,5




2
х

x2



х
у
0
у=

подтвердилась.
Я не только вспомнил графический способ, но и научился

решать уравнения и неравенства аналитическим методом и строить графики с несколькими модулями.
В дальнейшем можно рассмотреть аналитический метод решения неравенств и уравнений с модулем и параметром.