Презентация на тему Функция у=х в степени n , график и свойства

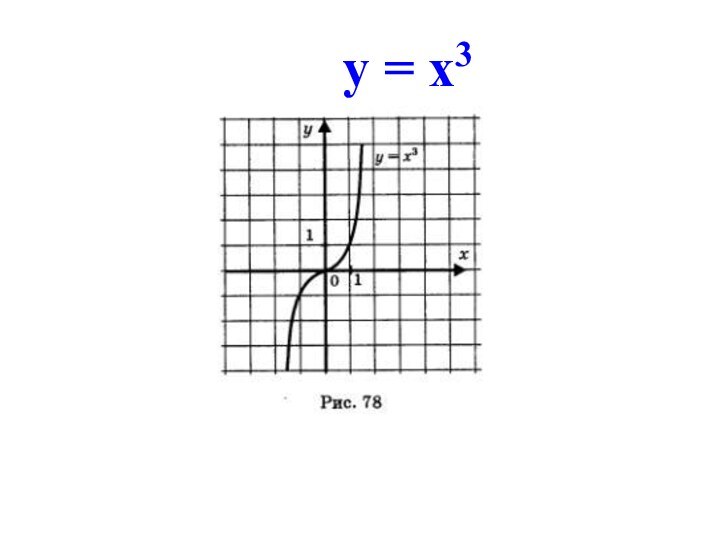
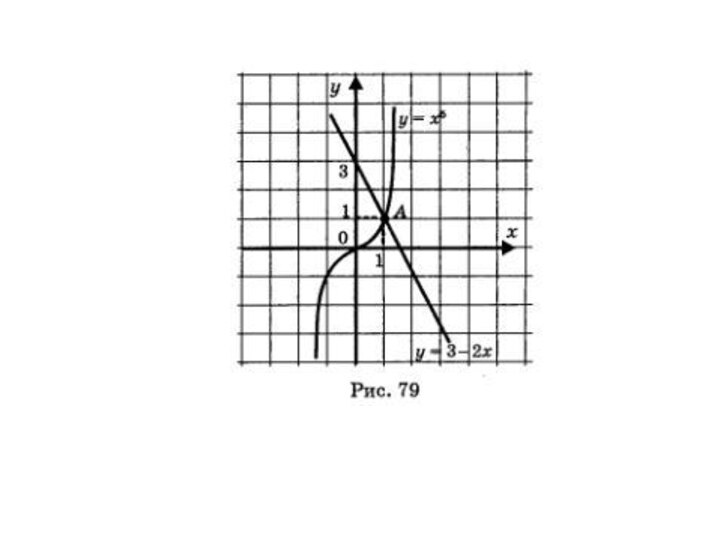
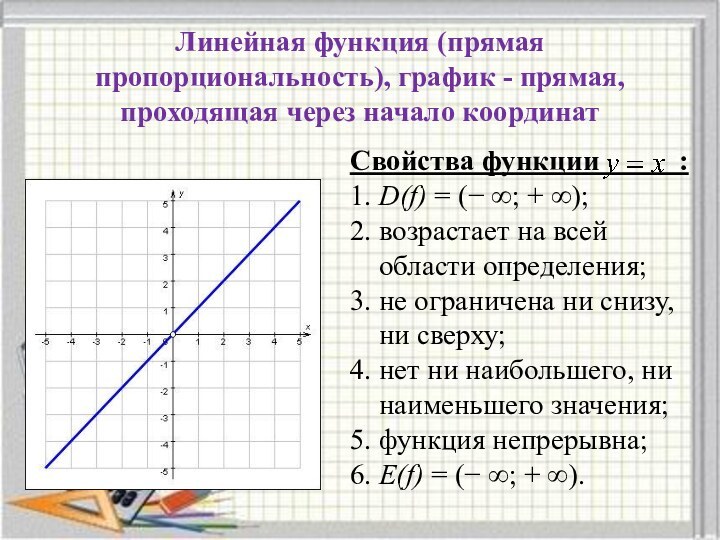
через начало координат

Свойства функции

:
1. D(f) = (− ∞; + ∞);
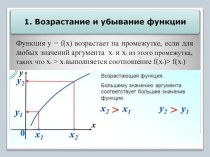
2. возрастает на всей
области определения;
3. не ограничена ни снизу,
ни сверху;
4. нет ни наибольшего, ни
наименьшего значения;
5. функция непрерывна;
6. Е(f) = (− ∞; + ∞).

в начале координат и которая направлена ветвями вверх
Свойства функции

:
1. D(f) = (− ∞; + ∞);
2. убывает на луче (− ∞; 0],
возрастает на луче [0; + ∞)
3. ограничена снизу, не
ограничена сверху;
4. Унаим. = 0, Унаиб. - не
существует;
5. функция непрерывна;
6. Е(f) = [0; + ∞);
7. выпукла снизу.

их свойства и графики».

1, 2, 3, 4, 5, …, называют степенной функцией

с натуральным показателем.

убывает(-∞, 0], возрастает [0; +∞) ;
Ограничена снизу, не ограничена

сверху;
У наим.= 0, У наиб. нет;
непрерывна;
Е(у) = [0, +∞);
выпукла вниз.

= х6, у = х8 и вообще о степенной функции

счетным показателем степени.
График любой такой функции похож на график функции у = х4, только его ветви более круто направлены вверх.
Отметим еще, что кривая у = х2n касается оси х в точке (0; 0), т.е. одна ветвь кривой плавно переходит в другую, как бы прижимаясь к оси х.

возрастает;
не ограничена ни снизу, ни сверху;
нет ни наименьшего, ни

наибольшего значений;
непрерывна;
Е(у) = (-∞, +∞);
выпукла вверх при х < 0, выпукла вниз при х > 0.

= х3, у = х5  и вообще о степенной

функции с нечетным показателем степени (3, 5, 7, 9 и т.д.).
График любой такой функции похож на график у = х3 функции только чем больше показатель, тем более круто направлены вверх (и соответственно вниз) ветви графика.
Отметим еще, что кривая у =х2n+1 касается оси х в точке (0; 0).