- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Понятие цилиндра
Содержание
- 2. СодержаниеОткуда и как появился цилиндр?Что такое цилиндр?
- 3. Как появился цилиндр? И откуда?Существует много версий и легенд.Вот одна из них…
- 4. Научное пособие по истории создания цилиндраОсновано на реальных событиях…..
- 5. Жил-был на свете милый, школьник по имени Вова…..
- 6. Он очень любил геометрию, а особенно -
- 7. Кружки жили очень долго в его тетради и сдружились за это время….
- 8. Казалось, ничто не угрожало их счастью, и дружба переросла в любовь….
- 9. НО ВДРУГ…
- 10. Вова получил двойку по геометрии и со злости порвал тетрадь, разлучив бедных влюблённых!
- 11. И казалось, что счастье было потеряно навсегда…
- 12. Но, к счастью, мимо проходили ножницы! Они
- 13. Сначала, ножницы вырезали из листа бумаги прямоугольник…
- 14. И освободили из тетрадного плена кружочки….
- 15. Затем добрые ножницы позвали на помощь не менее добрый клей…
- 16. И произошло чудо…
- 17. Клей воссоединил влюблённых, склеив их с прямоугольником!
- 18. Вот так и появилось самое романтичное тело вращения на земле =)
- 19. А назвали его цилиндром. Угадайте, почему?
- 20. В честь шляпы, конечно!!!!
- 21. В XVIII веке цилиндр стал
- 22. Что такое цилиндр? Цилиндром называют
- 23. Объем цилиндраОбъем любого цилиндра вычисляется по формуле
- 24. Площадь поверхности цилиндраПлощадью полной поверхности цилиндра является
- 25. Сечения цилиндраЕсли секущая плоскость проходит через ось
- 26. Вписанный и описанный цилиндр Призма называется
- 27. Цилиндры вокруг нас«Я думаю, что никогда до
- 28. Цилиндры в архитектуреЦилиндры применялись в архитектуре с древнейших времен. Например, колонны чаще всего имели цилиндрическую форму.
- 29. И сегодня цилиндр – главный помощник архитектора в его работе.
- 30. Это здание находится в Тель-Авиве
- 31. А это строение находится в Лондоне.
- 32. Не правда ли захватывает дух?Главная
- 33. Задачи на тему «Цилиндр». 1.
- 34. Решение задач. №1. 1.S сечения равна произведению
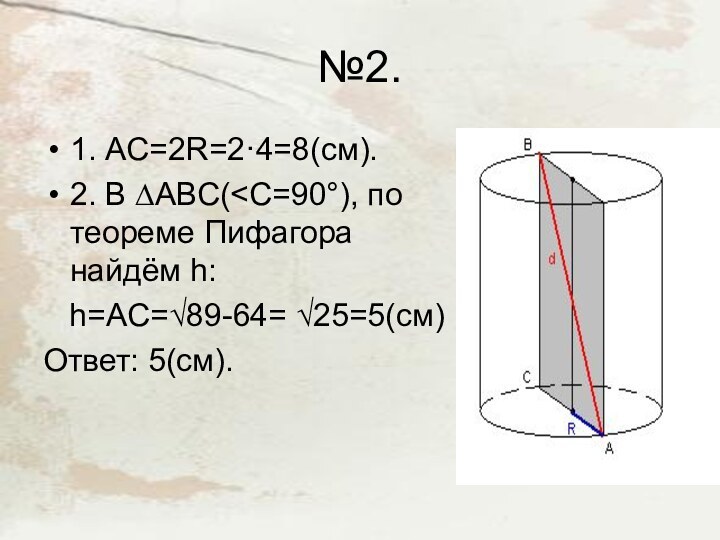
- 35. №2.1. АС=2R=2·4=8(см).2. В ∆АВС(
- 36. Скачать презентацию
- 37. Похожие презентации
СодержаниеОткуда и как появился цилиндр?Что такое цилиндр? Объем цилиндраПлощадь поверхности цилиндраСечения цилиндраВписанный и описанный цилиндрЦилиндры вокруг нас






























Слайд 6 Он очень любил геометрию, а особенно - тетрадку
по геометрии. Там он постоянно что-то рисовал…
И вот как-то
раз вместо домашнего задания Вова нарисовал в тетради два милых кружочка.Слайд 12 Но, к счастью, мимо проходили ножницы! Они увидели
горе кружков на разорванном листике и решили им помочь.
Слайд 21 В XVIII веке цилиндр стал мужским
головным убором. Новый головной убор в виде «трубы» на
голове шляпного торговца Джона Гетерингтона стал для чопорных англичан сенсацией. Тогдашние газеты писали: «Действие шляпы на прохожих было ужасным. Многие женщины при виде этого странного предмета лишались чувства, дети кричали...» А сам Гетерингтон был арестован и доставлен к лорду-мэру, который за нарушение общественного порядка приговорил его к штрафу в 500 фунтов стерлингов. Тем не менее эта прогулка по лондонской набережной 26 января 1797 года стала датой рождения нового направления моды. В начале XIX века цилиндр был исключительно аристократической принадлежностью.
Слайд 22
Что такое цилиндр?
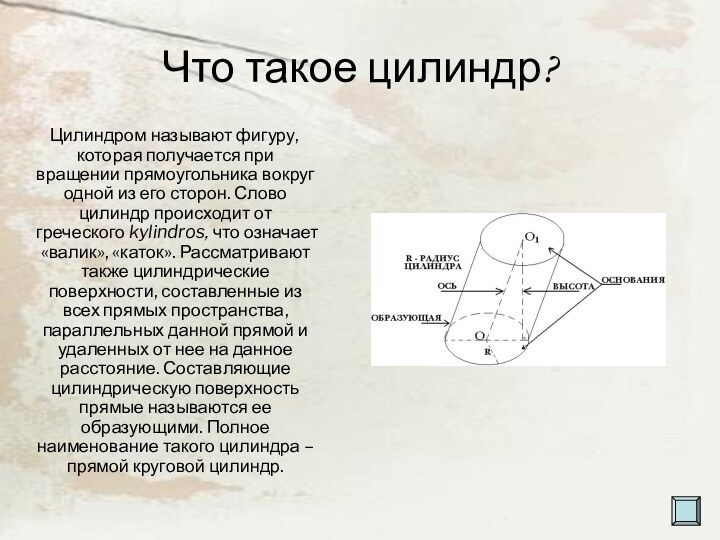
Цилиндром называют фигуру,
которая получается при вращении прямоугольника вокруг одной из его
сторон. Слово цилиндр происходит от греческого kylindros, что означает «валик», «каток». Рассматривают также цилиндрические поверхности, составленные из всех прямых пространства, параллельных данной прямой и удаленных от нее на данное расстояние. Составляющие цилиндрическую поверхность прямые называются ее образующими. Полное наименование такого цилиндра – прямой круговой цилиндр.
Слайд 23
Объем цилиндра
Объем любого цилиндра вычисляется по формуле
V
= SH,
где S – площадь основания m, а
H – высота, т.е. расстояние между плоскостями основания m и получающегося из m параллельным переносом на вектор xx’ второго основания m’.
Слайд 24
Площадь поверхности цилиндра
Площадью полной поверхности цилиндра является сумма
площадей боковой поверхности и двух оснований.
За площадь боковой поверхности
цилиндра принимается площадь ее развертки. Основание c прямоугольника является разверткой окружности основания цилиндра, а высота H – образующей цилиндра, поэтому c = 2 R, где R – радиус цилиндра, h – высота прямоугольника. Так как площадь прямоугольника равна S = 2 Rh, то для вычисления площади боковой поверхности цилиндра радиуса R и высоты h получаем формулуSбок = 2 Rh
Так как площадь каждого основания равна r2, то для нахождения полной поверхности цилиндра получаем формулу
Sцил= 2 r (r + h)
Слайд 25
Сечения цилиндра
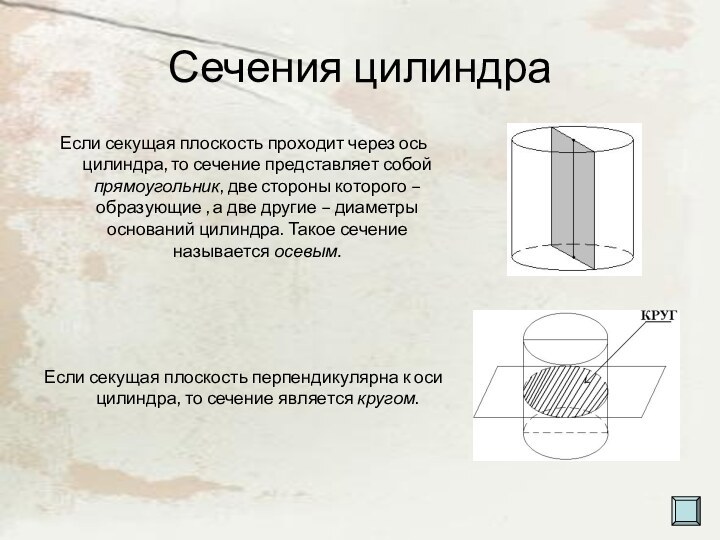
Если секущая плоскость проходит через ось цилиндра,
то сечение представляет собой прямоугольник, две стороны которого –
образующие , а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
Слайд 26
Вписанный и описанный цилиндр
Призма называется вписанной
в цилиндр, если основание её равные многоугольники, вписанные в
основание цилиндра, а боковые рёбра являются образующими цилиндра.Призма называется описанной около цилиндра, если её основание - это многоугольники описанные около основания цилиндра, а боковые грани касаются цилиндра.
Слайд 27
Цилиндры вокруг нас
«Я думаю, что никогда до настоящего
времени
мы не жили в такой геометрический период.
Все
вокруг - геометрия»Ле Корбюзье.
И правда, если мы посмотрим вокруг, мы увидим, что нас окружают одни лишь геометрические тела, в частности цилиндры.
Цилиндр может быть стаканом или гвоздем или быть частью архитектурной постройки или сложного механизма.
Слайд 28
Цилиндры в архитектуре
Цилиндры применялись в архитектуре с древнейших
времен. Например, колонны чаще всего имели цилиндрическую форму.
Слайд 33
Задачи на тему «Цилиндр».
1. Площадь
осевого сечения цилиндра равна 12 см², а высота цилиндра
– 2см. Найдите радиус основания.1. 3√2см. 2. 4 см. 3. 3 см. 4. другой ответ.
2. Диагональ осевого сечения цилиндра равна √89 см, а радиус основания – 4см. Найдите высоту цилиндра.
1. 3√5 см. 2. 6 см. 3. 5см. 4. другой ответ.
Слайд 34
Решение задач.
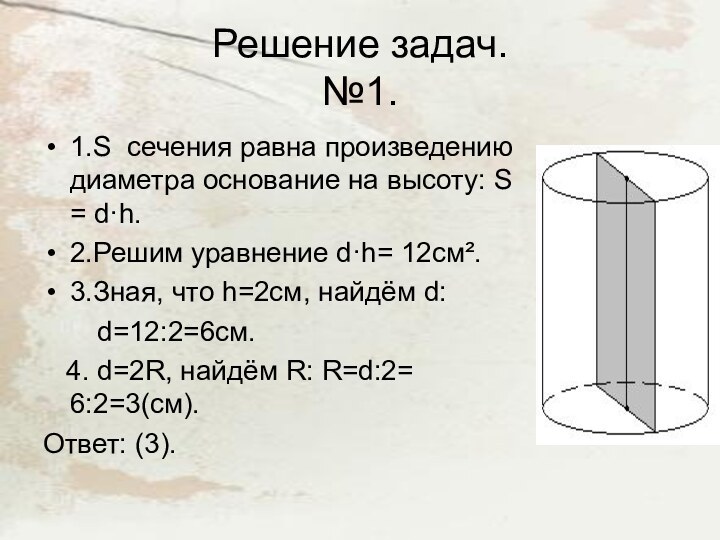
№1.
1.S сечения равна произведению диаметра основание
на высоту: S = d·h.
2.Решим уравнение d·h= 12см².
3.Зная,
что h=2cм, найдём d: d=12:2=6см.
4. d=2R, найдём R: R=d:2= 6:2=3(см).
Ответ: (3).