f(x) можно построить график функции y = - f(x)
?График функции
y = - f(x) получается из графика функции y = f(x) с помощью симметрии относительно оси Ох
Приведём примеры графиков
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


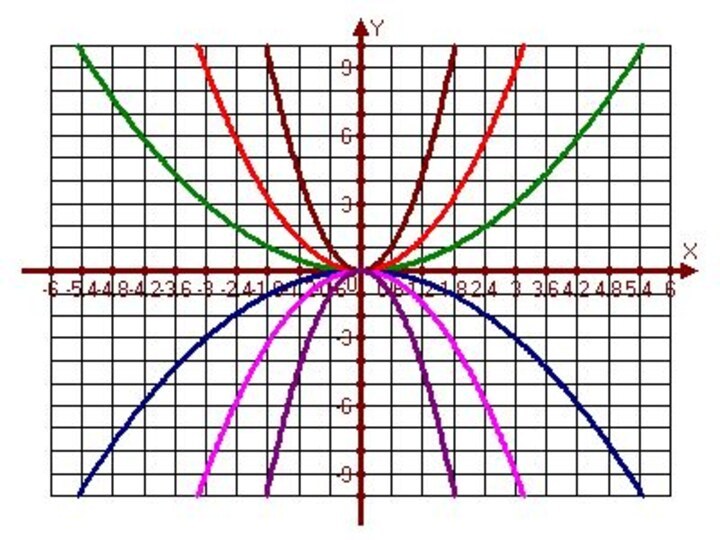
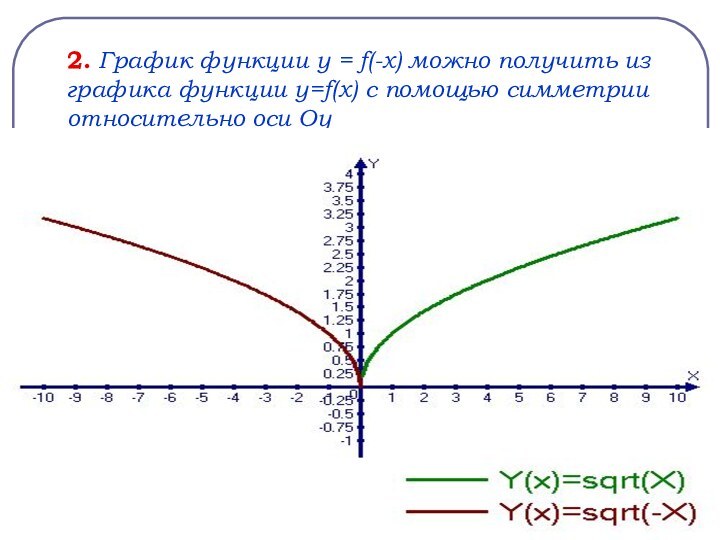


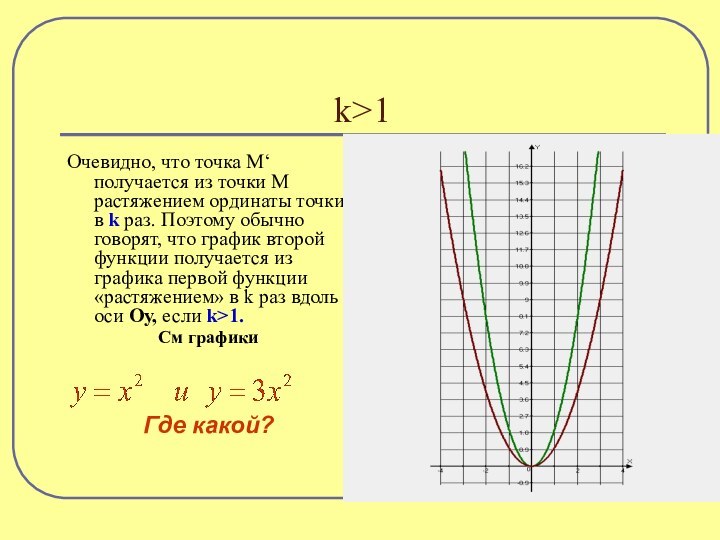

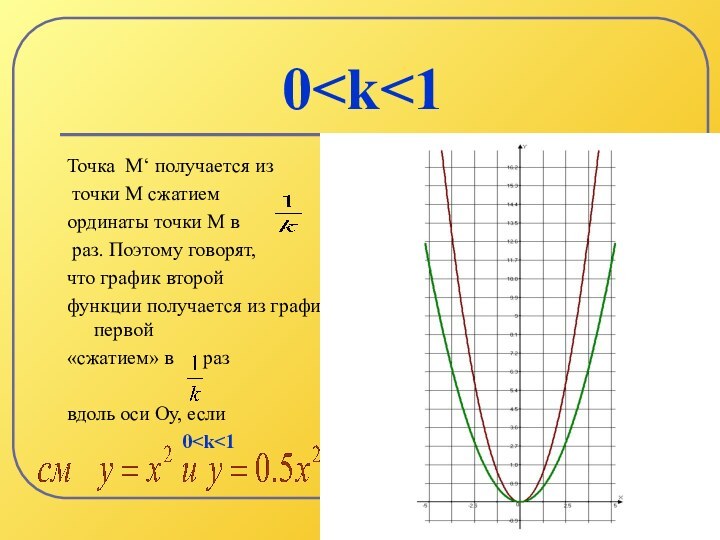


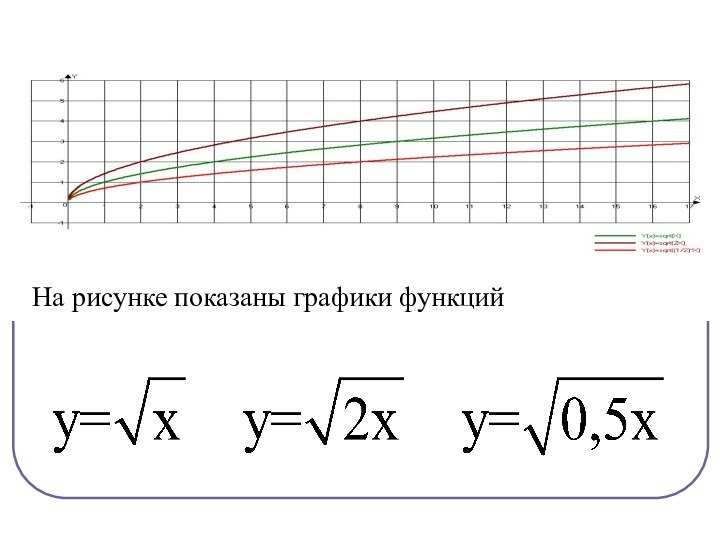



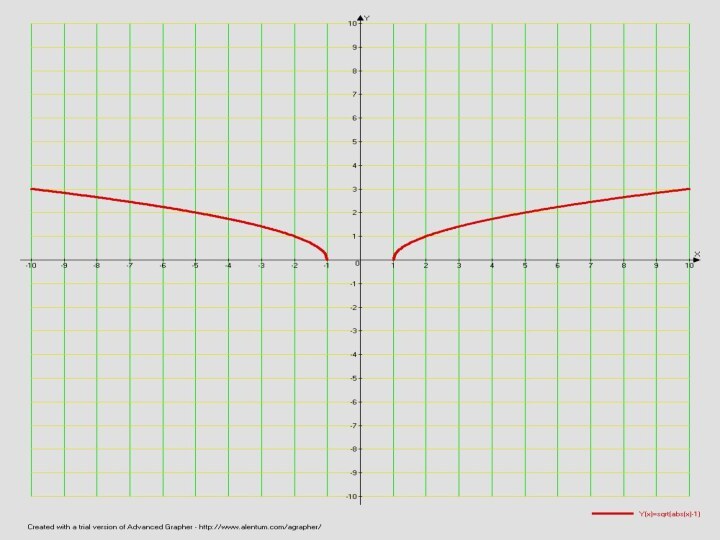

График функции
y = - f(x) получается из графика функции y = f(x) с помощью симметрии относительно оси Ох
Приведём примеры графиков
k>1