- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи на первый признак равенства треугольников
Содержание
- 2. Цель урокапознакомиться с первым признаком равенства треугольников
- 3. Практическое заданиеОтметьте в тетради любые три точки: А, В, С. Соедините их отрезками.Какая геометрическая фигура получилось?
- 4. ТреугольникТреугольник - простейшая плоская фигура. Которая состоит
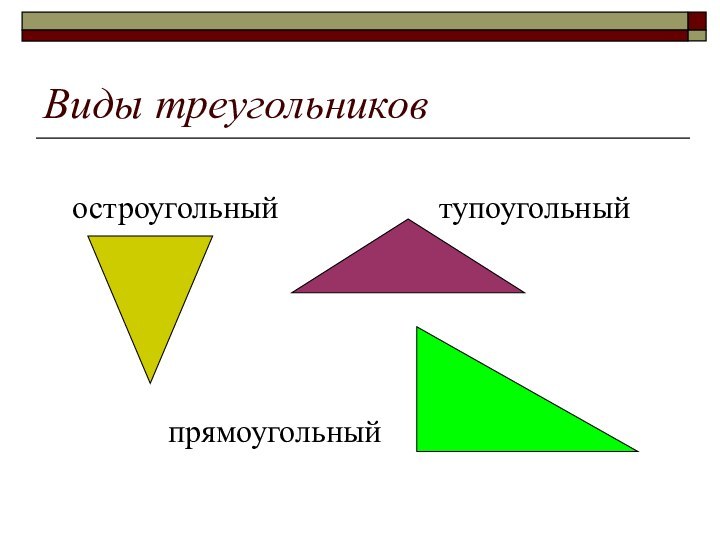
- 5. Виды треугольников остроугольный
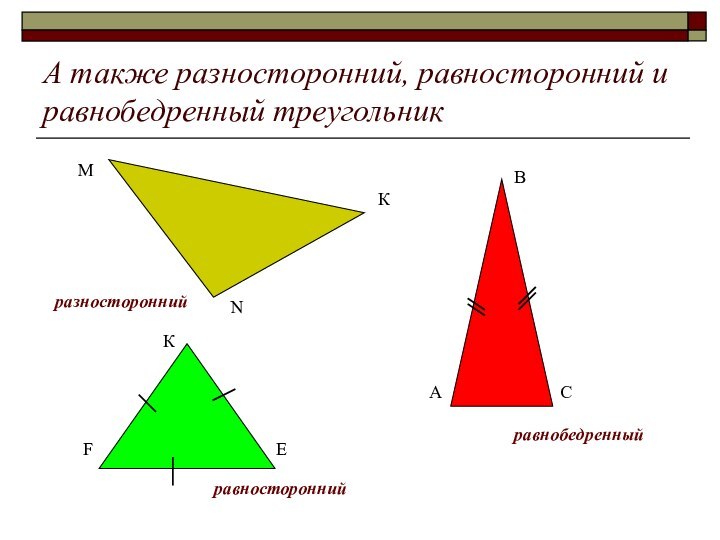
- 6. А также разносторонний, равносторонний и равнобедренный треугольникразностороннийМКNравностороннийравнобедренныйЕАСВКF
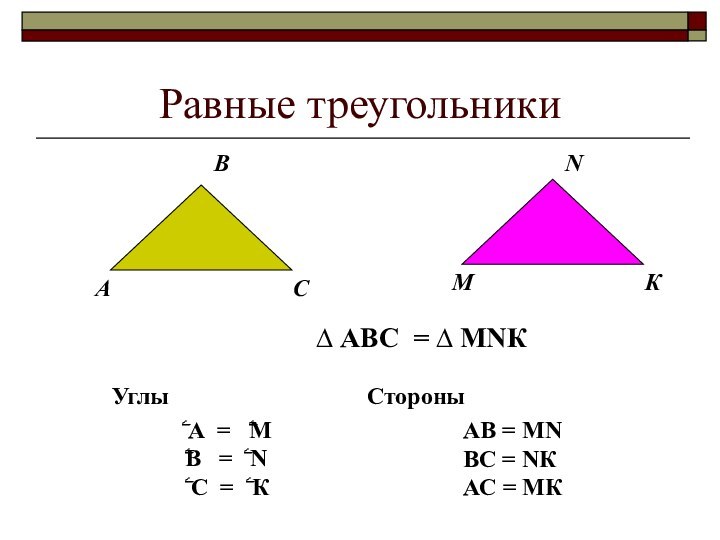
- 7. Равные треугольники АКМNСВ∆ АВС
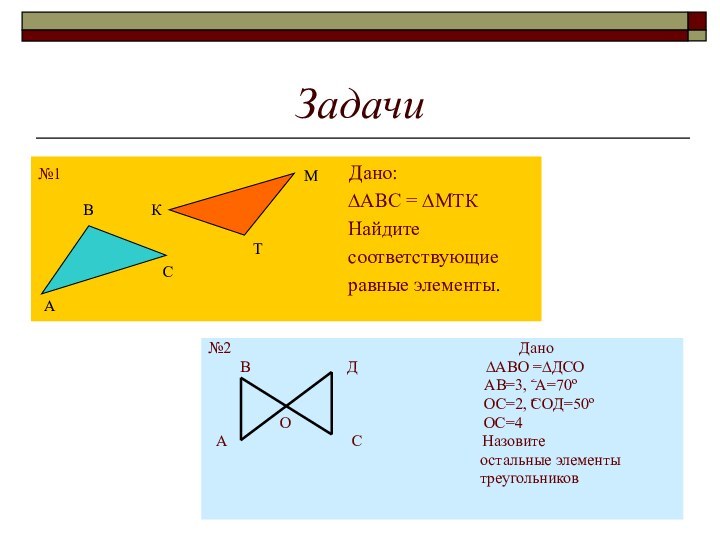
- 8. Задачи№2
- 9. Теорема:Если две стороны и угол между
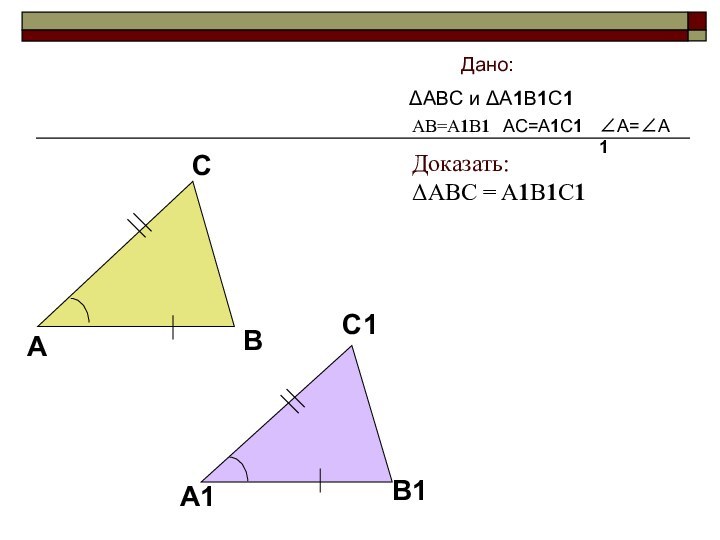
- 10. Дано: ABC и A1B1C1AC=A1C1A=A1AB=A1B1Доказать:ABC = A1B1C1
- 11. Доказательство:1 Рассмотрим ABC и A1B1C1Т.к. A=A1,
- 12. 2 Т.к. AB=A1B1, то сторона AB
- 13. 3 Итак, ABC и A1B1C1 полностью совместятся. Значит, треугольники равны.Теорема доказана.ABC = A1B1C1
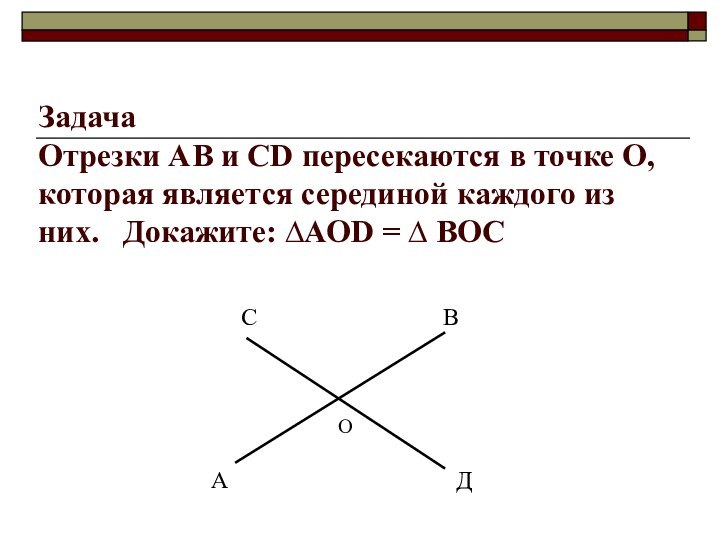
- 15. Задача Отрезки АВ и СD пересекаются в
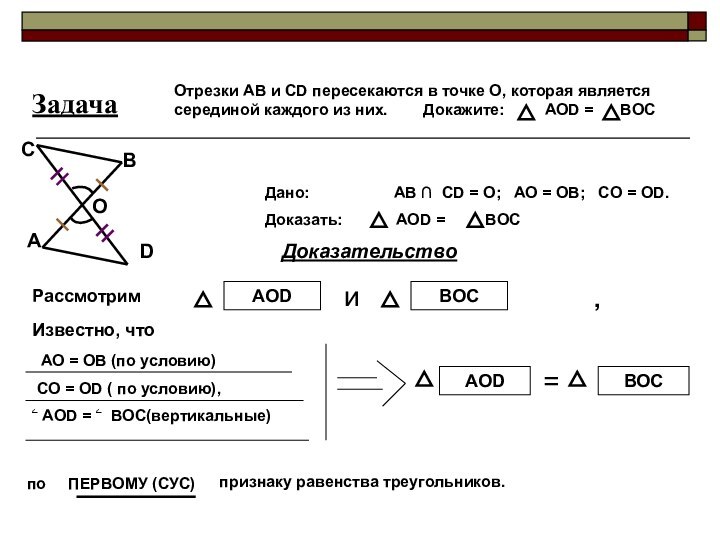
- 16. РассмотримAODиBOCИзвестно, что AO = OB (по
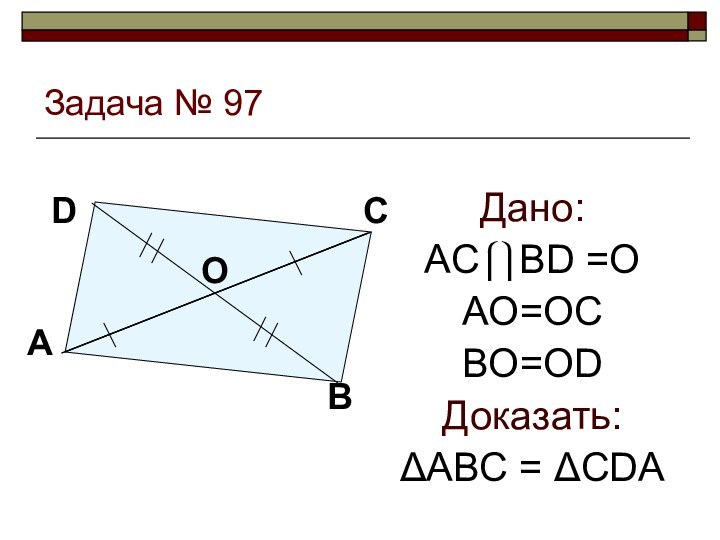
- 17. Задача № 97Дано: ACBD =OAO=OCBO=ODДоказать:ABC = CDA
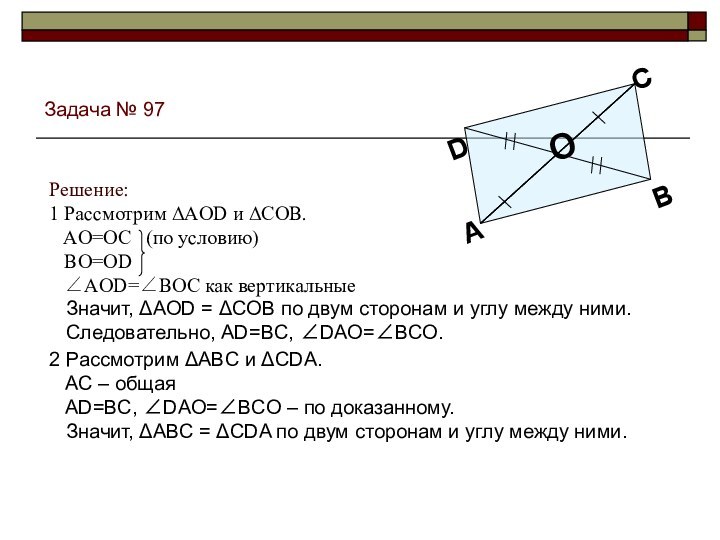
- 18. Задача № 972 Рассмотрим ABC и CDA.
- 19. Скачать презентацию
- 20. Похожие презентации







Слайд 2
Цель урока
познакомиться с первым признаком равенства треугольников и
его доказательством;
теорему о равенстве треугольников по двум сторонам и углу между ними
Слайд 3
Практическое задание
Отметьте в тетради любые три точки: А,
В, С.
Соедините их отрезками.
Какая геометрическая фигура получилось?
Слайд 4
Треугольник
Треугольник - простейшая плоская фигура. Которая состоит из
трех вершин (точки А, В, С ), трех сторон
( отрезки АВ, АС, ВС) и трех углов ( ۦ А ,ۦ В, ۦ С )∆ АВС
В
А
С
Слайд 6
А также разносторонний, равносторонний и равнобедренный треугольник
разносторонний
М
К
N
равносторонний
равнобедренный
Е
А
С
В
К
F
Слайд 7
Равные треугольники
А
К
М
N
С
В
∆ АВС =
∆ МNК
ۦ А = ۦМ
ۦВ = ۦ Nۦ С = ۦ К
АВ = MN
ВС = NК
АС = МК
Стороны
Углы
Слайд 8
Задачи
№2
Дано
В Д ∆АВО =∆ДСО
АВ=3, ۦ А=70º
ОС=2, ۦСОД=50º
О ОС=4
А С Назовите
остальные элементы
треугольников
№1 Дано:
∆АВС = ∆МТК
Найдите
соответствующие
равные элементы.
А
М
К
Т
С
В
Слайд 9
Теорема:
Если две стороны
и угол между ними
одного
треугольника соответственно равны двум сторонам и углу между ними
другого треугольника, то такие треугольники РАВНЫ
Слайд 11
Доказательство:
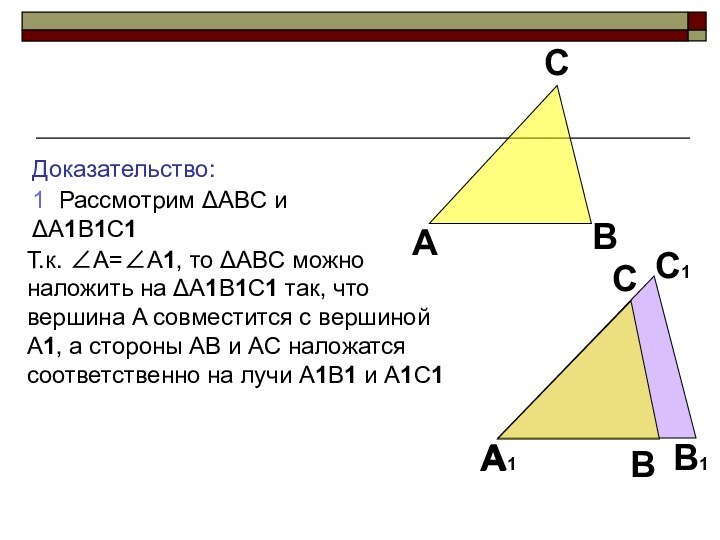
1 Рассмотрим ABC и A1B1C1
Т.к. A=A1, то
ABC можно наложить на A1B1C1 так, что вершина
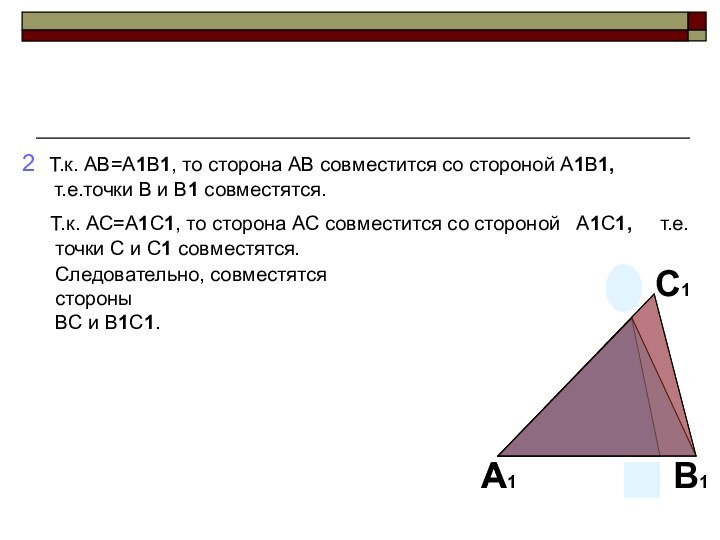
A совместится с вершиной A1, а стороны AB и AC наложатся соответственно на лучи A1B1 и A1C1Слайд 12 2 Т.к. AB=A1B1, то сторона AB совместится
со стороной A1B1, т.е.точки B
и B1 совместятся. Т.к. AC=A1C1, то сторона AC совместится со стороной A1C1, т.е.
точки C и C1 совместятся.
Следовательно, совместятся стороны
BC и B1C1.
Слайд 13
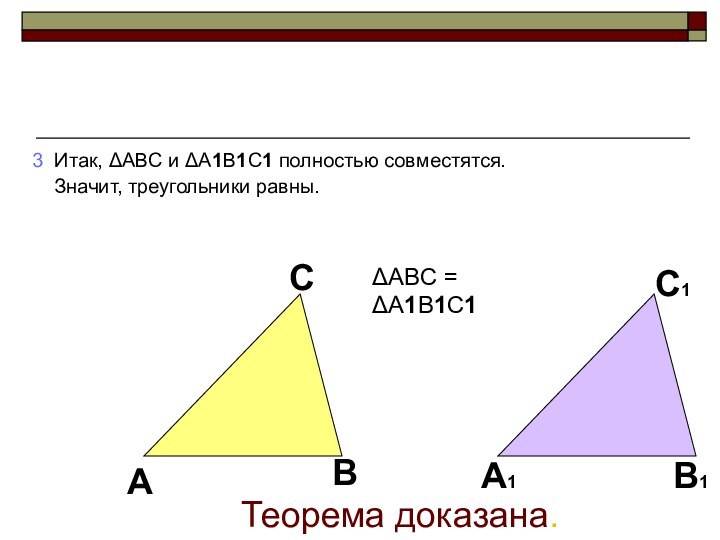
3 Итак, ABC и A1B1C1 полностью совместятся.
Значит, треугольники равны.
Теорема доказана.
ABC = A1B1C1
Слайд 14
Анализ
решения задач на доказательство равенства треугольников. Чтобы доказать, что
=
нужно найти у них 3 пары соответственно равных элементов.
Известно, что
Значит,
=
по
признаку равенства треугольников.
,
Слайд 15 Задача Отрезки АВ и СD пересекаются в точке О,
которая является серединой каждого из них. Докажите: ∆АОD
= ∆ ВOC С В
О
А Д
Слайд 16
Рассмотрим
AOD
и
BOC
Известно, что
AO = OB (по условию)
CO = OD ( по условию),
ۦ AOD = ۦ BOC(вертикальные)
AOD
=
BOC
по ПЕРВОМУ (СУС)
признаку равенства треугольников.
,
Задача
Отрезки АВ и СD пересекаются в точке О, которая является серединой каждого из них. Докажите: АОD = BOC
Дано: AB ∩ CD = O; AO = OB; CO = OD.
Доказать: AOD = BOC
Доказательство
D
А
В
С
О
Слайд 18
Задача № 97
2 Рассмотрим ABC и CDA.
AC – общая
AD=BC, DAO=BCO – по доказанному.
Значит, ABC = CDA по двум сторонам и углу между ними. Значит, AOD = COB по двум сторонам и углу между ними.
Следовательно, AD=BC, DAO=BCO.
Решение:
1 Рассмотрим AOD и COB.
AO=OC (по условию)
BO=OD
AOD=BOC как вертикальные





























