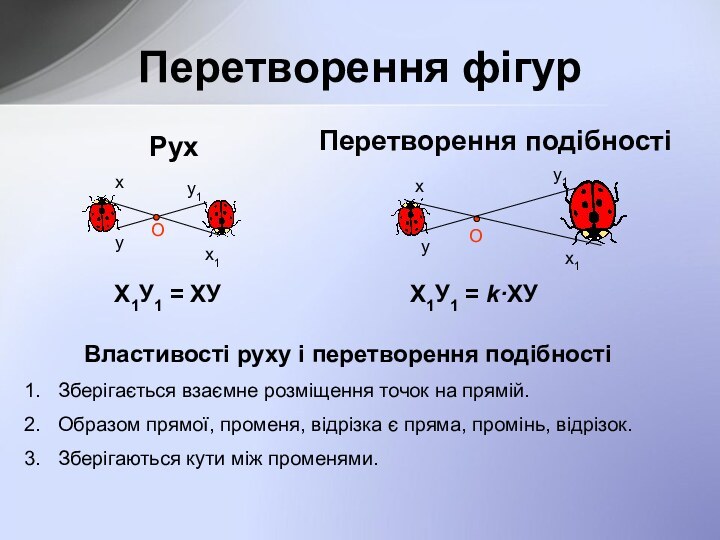
розміщення точок на прямій.
Образом прямої, променя, відрізка є пряма,
промінь, відрізок.Зберігаються кути між променями.
Х1У1 = ХУ
Х1У1 = k·ХУ
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометричні перетворення на площині
Содержание
- 2. Перетворення фігурРухПеретворення подібностіхух1у1Оху1ух1ОВластивості руху і перетворення подібностіЗберігається
- 3. Рівні і подібні фігуриРух ΔАВС = ΔА2В2С2
- 4. Перетворення фігур РухО – центр симетрії ОХ1=ОХ,
- 5. Перетворення фігур Перетворення подібностіО – центр гомотетії, OX1=k·OX, OУ1=k·OУХ1У1 = k·ХУХ1У1 = k·ХУ
- 6. Перевір себеНазвіть основні види вивчених перетворень фігур
- 7. Перетворення симетрії в координатній площиніf(-х)=f(x)Оу – вісь симетріїуf(-x) = -f(x)ОО – центр симетрії
- 8. Побудувати образ трапеції ABCD при симетрії з віссю Оу.Задача:(3;1)(1;1)(0;-1)(4;-1)Побудова
- 9. B1(4;-4)С(-2;1)A1(4;-1)C1(2;-1)А(-4;1)В(-4;4)Задача:Побудова Побудувати образ трикутника АВС при симетрії з центром у початку координат.
- 10. Паралельне перенесення в координатній площиніАВ(х,у)А1В1(х',у')хух' = х+а,у' = у+b
- 11. А(-6:3)В(-1;3)С(-2;1)D(-5;1)Побудувати образ трапеції ABCD при паралельному перенесенні на вектор a (4;-4).Задача:ПобудоваA1(-2:-1)B1(3;-1)C1(2;-3)D1(-1;-3)
- 12. Задача:Побудувати образ трапеції ABCD при паралельному перенесені на вектор АD (на вектор ВС).А(-6;1)В(-4;3)С(-3;3)D(-1;1)Відповідь:1 варіант2 вариантПеревір себе
- 13. C1(2;3)D1(4;1)B1(1;3)A1(-1;1)1 варіант (відповідь)АВСD
- 14. A1 (-5;1)B1 (-3;3)C1(-2;3)D1(0;1)2 варіант (відповідь)
- 15. MNN1M1Поворот в координатній площиніху0Поворот на 180о є центральна симетрія
- 16. 11XY0А(-4:-1)В(-5;3)D(-1;1)С(-1;3)A1(1;4)B1(3;5)C1(3;1)D1(1;1)Задача:Побудувати образ трапеції АВСD при повороті на 90о навколо О(0,0) за годинниковою стрілкою.Побудова
- 17. Перетворення подібності у координатній площиніПеретворення подібностіA (x,
- 18. B1(2;-2)С(-2;1)A1(2;-1/2)C1(1;-1/2)А(-4;1)В(-4;4)Задача:ПобудоваПобудувати образ трикутника АВС при гомотетії з центром О(0,0) і k=-1/2 .
- 19. Скачать презентацию
- 20. Похожие презентации
Перетворення фігурРухПеретворення подібностіхух1у1Оху1ух1ОВластивості руху і перетворення подібностіЗберігається взаємне розміщення точок на прямій.Образом прямої, променя, відрізка є пряма, промінь, відрізок.Зберігаються кути між променями.Х1У1 = ХУХ1У1 = k·ХУ
Слайд 2
Перетворення фігур
Рух
Перетворення подібності
х
у
х1
у1
О
х
у1
у
х1
О
Властивості руху і перетворення подібності
Зберігається взаємне
розміщення точок на прямій.
промінь, відрізок.Зберігаються кути між променями.
Слайд 3
Рівні і подібні фігури
Рух
ΔАВС = ΔА2В2С2 ,
тобто
∠А = ∠А2 АВ = А2В2
∠В = ∠В2 ВС = В2С2
∠С
= ∠С2 АС = А2С2
Слайд 4
Перетворення фігур
Рух
О – центр симетрії ОХ1=ОХ,
ОY1=ОУ
Х1У1 =
ХУ
l – вісь симетрії, МХ1=МХ, РY1=РY XX1⊥l, YY1⊥l
Х1У1 =
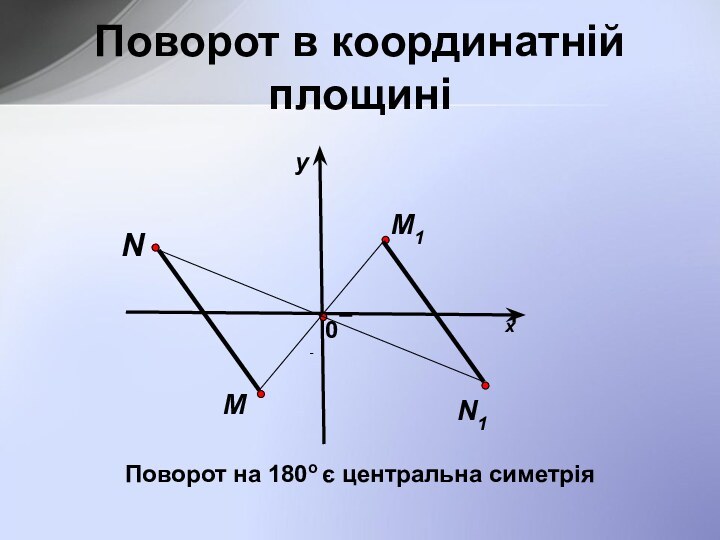
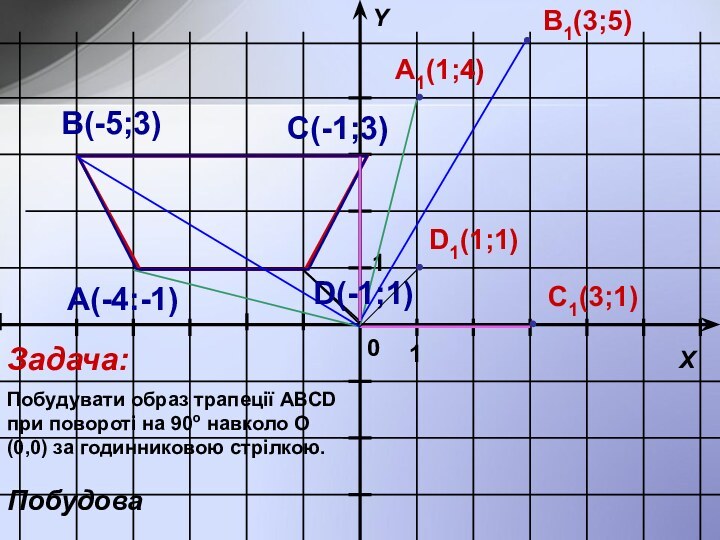
ХУО–центр повороту ∠ХОХ1=∠YOY1=α,OX1=OX, OY1=OY
Х1У1 = ХУ
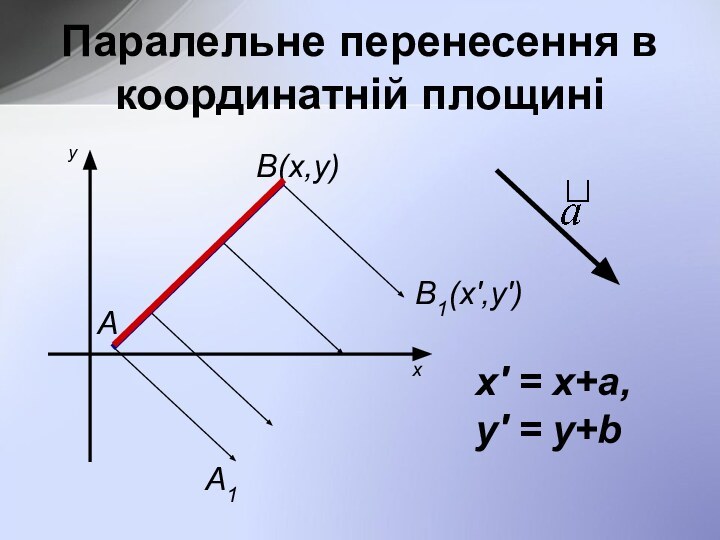
l – напрямлений вектор, ХХ1⎪⎪l, YY1 ⎪⎪l, X1=YY1=l
Х1У1 = ХУ
Слайд 5
Перетворення фігур
Перетворення подібності
О – центр гомотетії,
OX1=k·OX, OУ1=k·OУ
Х1У1
= k·ХУ
Х1У1 = k·ХУ
Слайд 6
Перевір себе
Назвіть основні види вивчених перетворень фігур і
дайте їм визначення.
На кругах Ейлера є інформація про поняття
різних видів перетворень фігур. Які з тверджень правильні:а) гомотетія є перетворення подібності;
б) перетворення подібності є гомотетія;
в) рух є перетворення подібності;
г) перетворення подібності є рух?
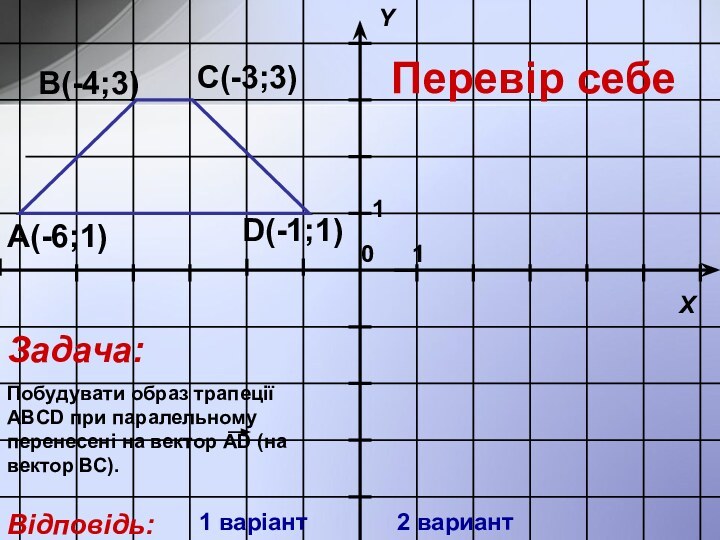
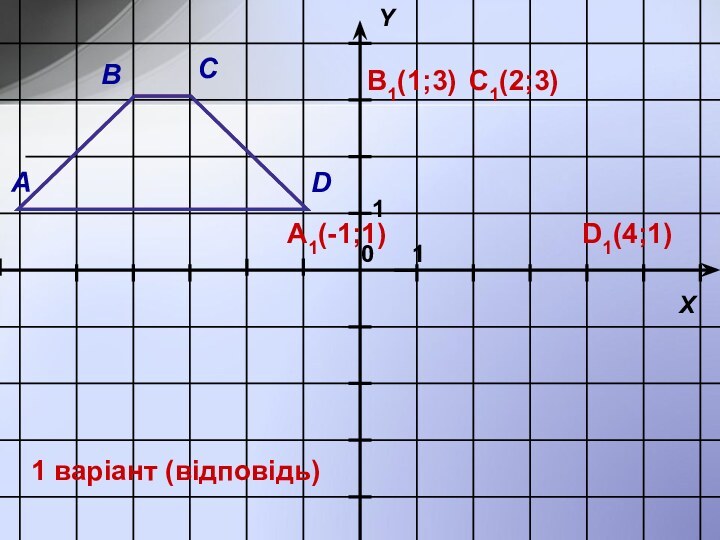
Відповіді:
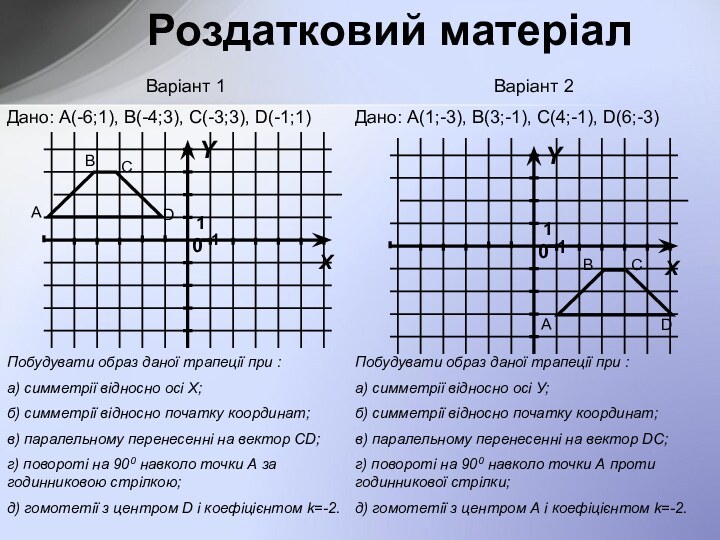
Рух і перетворення подібності.
а), в).
Слайд 7
Перетворення симетрії в координатній площині
f(-х)=f(x)
Оу – вісь симетрії
у
f(-x)
= -f(x)
О
О – центр симетрії
Слайд 8
Побудувати образ трапеції ABCD при симетрії з віссю
Оу.
Задача:
(3;1)
(1;1)
(0;-1)
(4;-1)
Побудова
Слайд 9
B1(4;-4)
С(-2;1)
A1(4;-1)
C1(2;-1)
А(-4;1)
В(-4;4)
Задача:
Побудова
Побудувати образ трикутника АВС при симетрії з
центром у початку координат.
Слайд 11
А(-6:3)
В(-1;3)
С(-2;1)
D(-5;1)
Побудувати образ трапеції ABCD при паралельному перенесенні на
вектор a (4;-4).
Задача:
Побудова
A1(-2:-1)
B1(3;-1)
C1(2;-3)
D1(-1;-3)
Слайд 12
Задача:
Побудувати образ трапеції ABCD при паралельному перенесені на
вектор АD (на вектор ВС).
А(-6;1)
В(-4;3)
С(-3;3)
D(-1;1)
Відповідь:
1 варіант
2 вариант
Перевір себе
Слайд 16
1
1
X
Y
0
А(-4:-1)
В(-5;3)
D(-1;1)
С(-1;3)
A1(1;4)
B1(3;5)
C1(3;1)
D1(1;1)
Задача:
Побудувати образ трапеції АВСD при повороті на 90о
навколо О(0,0) за годинниковою стрілкою.
Побудова
Слайд 17
Перетворення подібності у координатній площині
Перетворення подібності
A (x, y)
A1(х1, y1)
х1 = kx, k ≠ 0
y1=ky,
Гомотетія
A
(x, y) A2(х2, y2)х2 = kx, k ≠ 0
y2=ky
Слайд 18
B1(2;-2)
С(-2;1)
A1(2;-1/2)
C1(1;-1/2)
А(-4;1)
В(-4;4)
Задача:
Побудова
Побудувати образ трикутника АВС при гомотетії з центром
