Презентация на тему Графики квадратичной функции

при a=1
при a= -1
1 2 3 4

5 6

-6 -5-4-3-2-1

1

4

9

-9

-4

квадратичной функции

графики функций:

графики функций:

х²+4
У= (х+7)² - 9
У=6 х²
(4;5)
(1;0)
(0;12)
(0;4)
(-7;-9)
(0;0)

функции, его свойства

вида y=ax²+bx+c, где х - независимая переменная, a,

b и с -некоторые числа (причём а≠0).

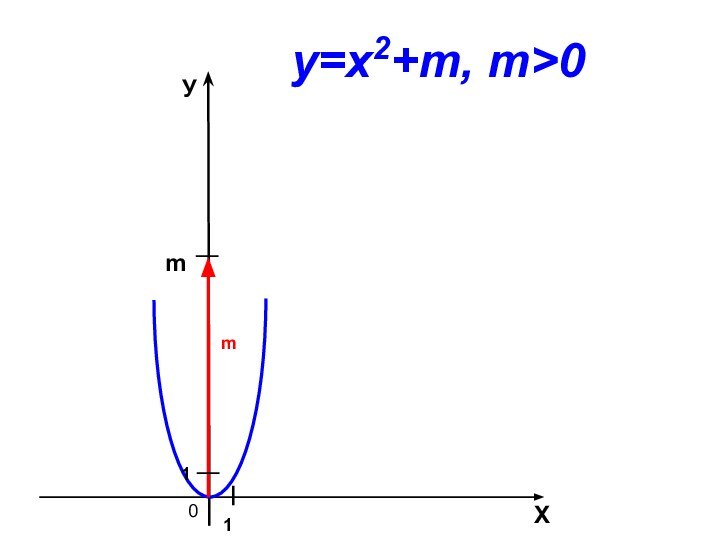
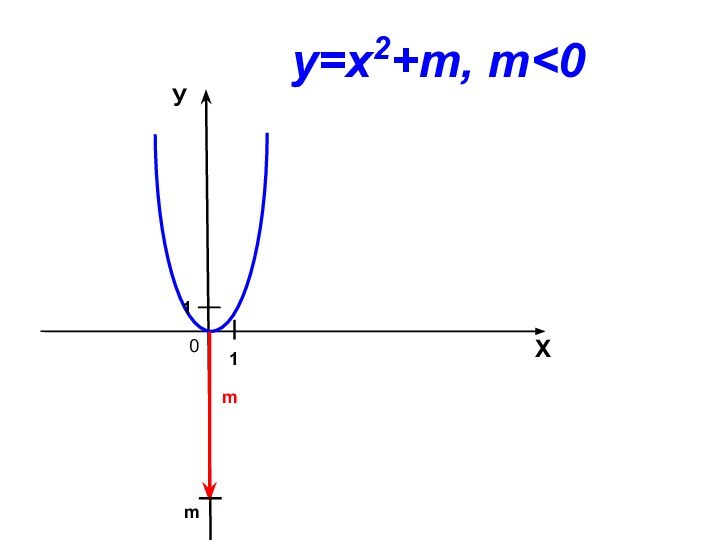
Например: у = 5х²+6х+3,
у = -7х²+8х-2,
у = 0,8х²+5,
у = ¾х²-8х,
у = -12х²
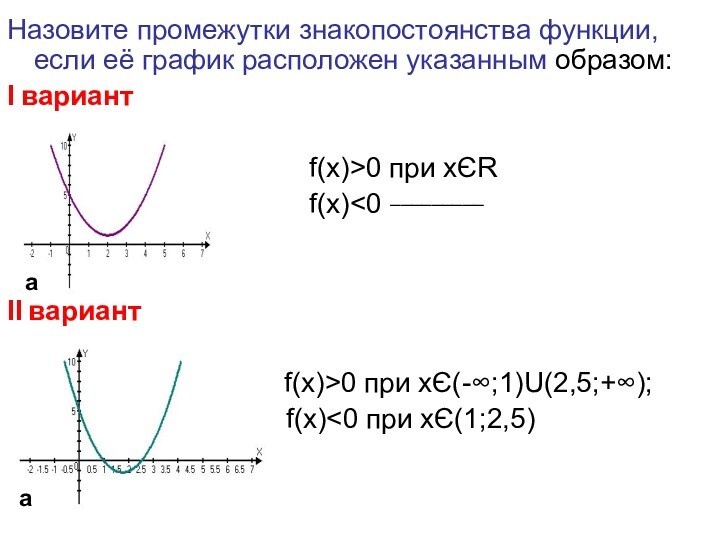
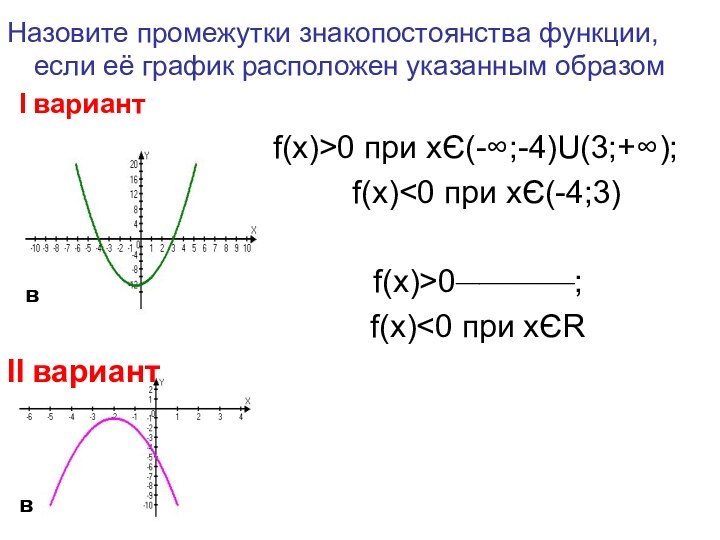
квадратичные функции

вверх(если а>0) или вниз (если а

парабола, ветви которой направлены вверх (т.к. а=2, а>0).

у= -7х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а<0).

у


0
х

у


0
х

на координатной плоскости.
Через вершину параболы начертить ось симметрии

параболы
Найти нули функции и 0тметить их на числовой прямой
Найти координаты двух дополнительных точек и симметричных им
Провести кривую параболы.

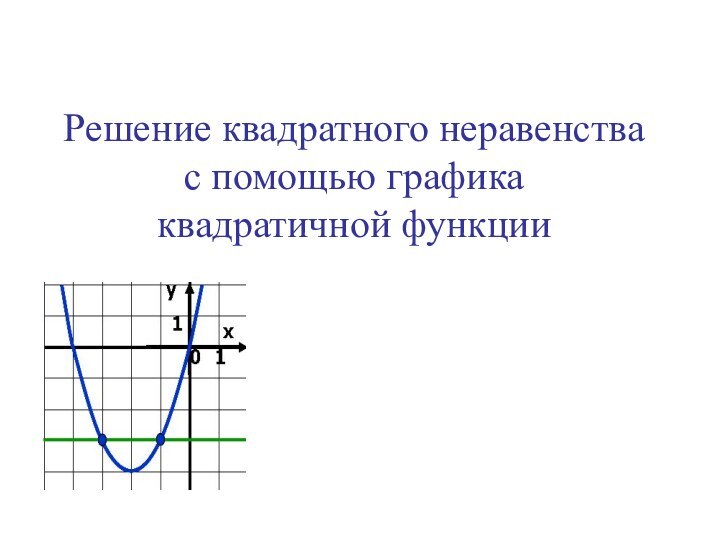
Алгоритм решения

если х
4. у↓, если х
у↑, если х
5.

унаим= -8, если х= -1

унаиб – не существует.

6. Е(y):

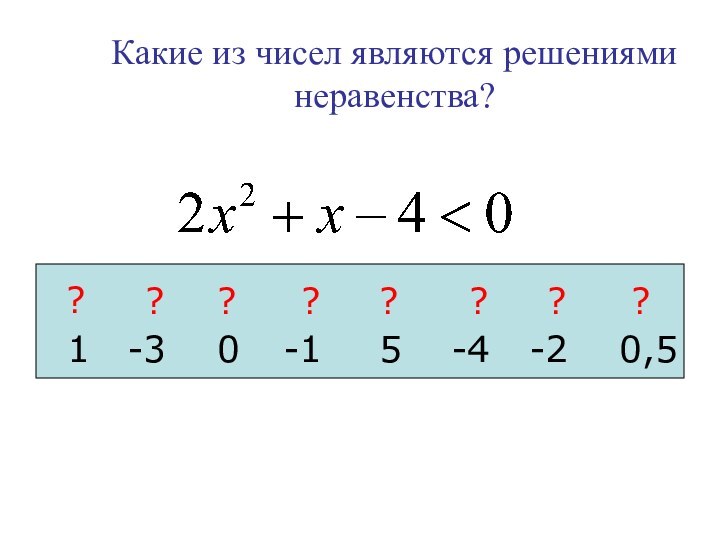
Проверь себя:

у<0, если х

степени, а правая- нуль, называется неравенством второй степени.
Все квадратные

неравенства могут быть приведены к одному из следующих видов:
1) ах2+bx+c>0; 2) ах2+bx+c<0;
3) ах2+bx+c≥0; 4) ах2+bx+c≤0.

второй степени:
1) 6х 2-13х>0;

2) x 2-3x-14>0;

3) (5+x)(x-4)>7; 4) ;

5)

6) 8x2 >0; 7) (x-5)2 -25>0;

и знак коэффициента а, если график соответствующей квадратичной функции

расположен следующим образом:

е

а

б

в

г

д

указанным образом:
Ι вариант.




ΙІ вариант.
в
б
а
а
в
б

указанным образом:
Ι вариант

f(x)>0 при xЄR
f(x)<0 _________


ΙІ вариант

f(x)>0 при xЄ(-∞;1)U(2,5;+∞);
f(x)<0 при xЄ(1;2,5)

а

а

указанным образом:

Ι вариант

f(x)>0 при xЄ(-∞;-3)U(-3;+∞)
f(x)<0__________

ΙІ вариант


f(x)>0 при xЄ(-∞;0,5)U(0,5;+∞)
f(x)<0 __________

б

б

указанным образом
Ι вариант

f(x)>0 при xЄ(-∞;-4)U(3;+∞);
f(x)<0 при xЄ(-4;3)

f(x)>0__________;
f(x)<0 при xЄR
ΙІ вариант

в

в

функцию
y=5х2+9х-2
3. Графиком функции является парабола, ветви которой направлены

вверх.
4. 5х2+9х-2=0

х1=-2; х2=
5.

-2

0

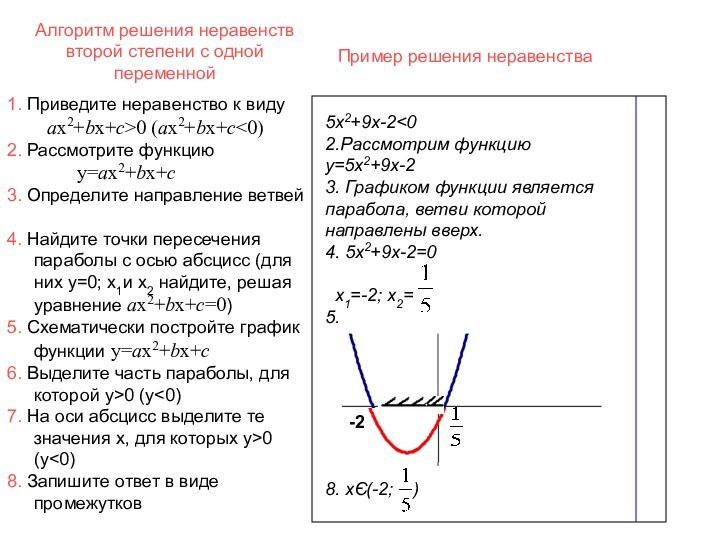
1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей


4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х1и х2 найдите, решая уравнение ax2+bx+c=0)
5. Схематически постройте график функции y=ax2+bx+c
6. Выделите часть параболы, для которой y>0 (y<0)

Пример решения неравенства

функцию
y=5х2+9х-2
3. Графиком функции является парабола, ветви которой направлены

вверх.
4. 5х2+9х-2=0

х1=-2; х2=
5.

-2

0

1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей


4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х1и х2 найдите, решая уравнение ax2+bx+c=0)
5. Схематически постройте график функции y=ax2+bx+c
6. Выделите часть параболы, для которой y>0 (y<0)
7. На оси абсцисс выделите те значения х, для которых y>0 (y<0)

Пример решения неравенства

функцию
y=5х2+9х-2
3. Графиком функции является парабола, ветви которой направлены

вверх.
4. 5х2+9х-2=0

х1=-2; х2=
5.







8. хЄ(-2; )

-2

0

1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей

4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х1и х2 найдите, решая уравнение ax2+bx+c=0)
5. Схематически постройте график функции y=ax2+bx+c
6. Выделите часть параболы, для которой y>0 (y<0)
7. На оси абсцисс выделите те значения х, для которых y>0 (y<0)
8. Запишите ответ в виде промежутков

Пример решения неравенства

в таблице 2 - решение неравенства 2:
1.
2.
Таблица 1
а
в
с
d
а
в
с
d
Таблица

2

в таблице 2- решение неравенства 2:
1.
2.
Таблица 1
а
в
с
d
а
в
с
d
Таблица 2

в таблице 2- решение неравенства 2:
1.
2.
Таблица 1
а
в
с
d
а
в
с
d
Таблица 2

в таблице 2- решение неравенства 2:
1.
2.
Таблица 1
а
в
с
d
а
в
с
d
Таблица 2

систематизировать знания о применении квадратичной функции. Математика- это содержательное,

увлекательное и доступное поле деятельности, дающее ученику богатую пищу для ума. Свойства квадратичной функции лежат в основе решения квадратных неравенств. Многие физические зависимости выражаются квадратичной функцией; например, камень, брошенный вверх со скоростьюv0, находится в момент времени t на расстоянии
s(t)=-q\2t2+v0t
от земной поверхности (здесь q- ускорение силы тяжести);
количество тепла Q, выделяемое при прохождении тока в проводнике с сопротивлением R, выражается через силу тока I формулой
Q=RI2.
Знания свойств квадратичной функции позволяют рассчитать дальность полета тела, брошенного вертикально вверх или под некоторым углом. Этим пользуются в оборонной промышленности.

предложений, которое больше других соответствует вашему состоянию.
“Выполнять

задания и решать задачи мне трудно, так как …”
“Выполнять задания и решать задачи мне легко, так как …”
“Выполнять задания и решать задачи для меня занятие приятное и интересное, потому что…”