- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Индексный метод
Содержание
- 2. Вопросы для рассмотрения:Понятие статистического индекса.Классификация статистических индексов.Расчет статистических индексов.
- 3. 1. Понятие статистического индексаСтатистический индекс (J)– это
- 4. Сущность индексаИндекс – это относительная величи на
- 5. Задачи, решаемые с помощью статистических индексов:Определение средних
- 6. Задачи, решаемые с помощью статистических индексов:Оценка средней
- 7. Задачи, решаемые с помощью статистических индексов:Установка среднего
- 8. 2. Классификация статистических индексов1.В зависимости от степени охвата обобщаемых единиц изучаемой совокупности индексы подразделяются на:индивидуальные (элементарные);групповые;общие.
- 9. Индивидуальные индексы -индексы, характеризующие изменения отдельных единиц
- 10. Групповые индексы -индексы, охватывающие часть элементов сложного явления.Пример: индексы цен по группам продовольственных и непродовольственных товаров.
- 11. Общие индексы -индексы, выражающие сводные (обобщающие) результаты
- 12. Свойства общих индексов:синтетические свойства: посредством индексного метода
- 13. Классификация индексов По экономическому назначению:динамические – индексы,
- 14. Классификация индексовПо базе сравнения:базисные индексы – индексы
- 15. Классификация индексовПо базе сравнения:цепные индексы – индексы,
- 16. Классификация индексовПо виду весов:индексы с постоянными весами
- 17. Классификация индексовПо форме построения:индивидуальные;агрегатные;средние.
- 18. Классификация индексовПо объекту исследования:производительность труда;себестоимость продукции, услуг;объем продукции;зарплата и др.
- 19. Классификация индексовПо составу явления:постоянные;переменные.
- 20. Основные категории индексного отношения:Индексируемая величина – значение
- 21. Основные категории индексного отношения:Соизмерители – специальные сомножители
- 22. Основные категории индексного отношения:Свойства соизмерителей:необходимы для перехода
- 23. Соизмерители индексируемых величин -экономические показатели:цена (p);количество (физический
- 24. Классификация индексовАгрегатный индекс – сложный относительный показатель,
- 25. Виды агрегатных индексов:Индекс Пааше – характеризует влияние
- 26. Виды агрегатных индексов:Индекс Ласпейреса –характеризует влияние изменения
- 27. 3.Расчет статистических индексовРасчет индивидуальных индексов:цен: Jp
- 28. Расчет индексов:Расчет индекса товарооборота:
- 29. Расчет агрегатных индексов:Индекс Пааше:
- 30. Пример расчета статистических индексов. Индексный факторный
- 31. Пример расчета статистических индексов
- 32. Пример расчета статистических индексовЗадание :Определить динамику цен,
- 33. Пример расчета статистических индексов1. Индивидуальные индексы цен
- 34. Расчет индивидуальных индексов ценJpн = (663/ 470)
- 35. Пример расчета статистических индексов2. Индивидуальные индексы физического
- 36. Расчет индивидуальных индексов физического объема: Jgн =(243/258)
- 37. Пример расчета статистических индексов3. Индивидуальные индексы товарооборота
- 38. Расчет индивидуальных индексов товарооборота:
- 39. Пример расчета статистических индексов1.Агрегатный индекс объема товарооборота
- 40. Расчет агрегатного индекса товарооборота:
- 41. Расчет агрегатного индекса товарооборота:Абсолютное изменение товарооборота в
- 42. Пример расчета статистических индексов2. Агрегатный индекс цен
- 43. Расчет агрегатного индекса цен:
- 44. Расчет агрегатного индекса цен:Абсолютное изменение товарооборота в
- 45. Пример расчета статистических индексов3. Агрегатный индекс физического
- 46. Расчет агрегатного индекса физического объема:
- 47. Расчет агрегатного индекса физического объема:Абсолютное изменение товарооборота
- 48. Скачать презентацию
- 49. Похожие презентации
Вопросы для рассмотрения:Понятие статистического индекса.Классификация статистических индексов.Расчет статистических индексов.















































Слайд 2
Вопросы для рассмотрения:
Понятие статистического индекса.
Классификация статистических индексов.
Расчет статистических
индексов.
Слайд 3
1. Понятие статистического индекса
Статистический индекс (J)– это относительный
показатель, вариант соотношения величин какого либо явления во времени,
пространстве или сравнение фактических данных с эталоном (планом).
Слайд 4
Сущность индекса
Индекс – это относительная величи на сравнения
сложных совокупностей и отдельных их единиц.
При этом под
сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию.
Слайд 5
Задачи, решаемые с помощью статистических индексов:
Определение средних изменений
сложных, непосредственно несоизмеримых совокупностей во времени. Здесь индексы выступают
в виде показателей динамики;При изучении динамики социально-экономических явлений сравниваемая величина (числитель индексного отношения) принимается за текущий (или отчетный) период, а величина, с которой производится сравнение – за базисный период.
Слайд 6
Задачи, решаемые с помощью статистических индексов:
Оценка средней степени
выполнения плана по совокупности в целом или ее части,
при которой индексы определяются в виде показателей выполнения плана;
Слайд 7
Задачи, решаемые с помощью статистических индексов:
Установка среднего соотношения
сложных явлений в пространстве. Индексы – показатели сравнения;
Определение роли
отдельных факторов в общем изменении сложных явлений во времени или пространстве. Индексы – аналитический инструмент.
Слайд 8
2. Классификация статистических индексов
1.В зависимости от степени охвата
обобщаемых единиц изучаемой совокупности индексы подразделяются на:
индивидуальные (элементарные);
групповые;
общие.
Слайд 9
Индивидуальные индексы -
индексы, характеризующие изменения отдельных единиц статистической
совокупности.
В этом случае индексируемый признак в отчетном периоде сопоставляется
с базисным уровнем этого же признака.Пример: если при изучении оптовой реализации продовольственных товаров определяются изменения в продаже отдельных товарных разновидностей, то получают индивидуальные (однотоварные индексы).
Слайд 10
Групповые индексы -
индексы, охватывающие часть элементов сложного явления.
Пример:
индексы цен по группам продовольственных и непродовольственных товаров.
Слайд 11
Общие индексы -
индексы, выражающие сводные (обобщающие) результаты совместного
изменения всех единиц, образующих статистическую совокупность.
Пример: показатель изменения объема
реализации товарной массы продуктов питания по отдельным периодам будет общим индексом физического объема товарооборота.
Слайд 12
Свойства общих индексов:
синтетические свойства: посредством индексного метода производится
соединение (агрегирование) в целом разнородных единиц статистической совокупности;
аналитические свойства:
посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.
Слайд 13
Классификация индексов
По экономическому назначению:
динамические – индексы, отражающие
изменение состояния во времени;
территориальные – индексы, отражающие изменение состояния
явления в зависимости от месторасположения.
Слайд 14
Классификация индексов
По базе сравнения:
базисные индексы – индексы с
постоянной базой сравнения ( в знаменателе всех индексов находится
индексируемая величина базисного периода).Эти индексы характеризуют изменение явлений за длительный промежуток времени по отношению к какой-либо одной отправной точке.
Слайд 15
Классификация индексов
По базе сравнения:
цепные индексы – индексы, сопоставляемые
с разной базой сравнения и характеризующие текущие изменения явлений.
Слайд 16
Классификация индексов
По виду весов:
индексы с постоянными весами –
индексы, вычисленные с весами, не меняющимися при переходе
от одного индекса к другому;индексы с переменными весами – индексы, вычисленные с весами, меняющимися при переходе от одного индекса к другому.
Слайд 18
Классификация индексов
По объекту исследования:
производительность труда;
себестоимость продукции, услуг;
объем продукции;
зарплата
и др.
Слайд 20
Основные категории индексного отношения:
Индексируемая величина – значение признака
статистической совокупности, изменение которой является объектом изучения с помощью
индексного метода.Вес индекса – величина, служащая для целей соизмерения индексируемых величин.
Слайд 21
Основные категории индексного отношения:
Соизмерители – специальные сомножители индексируемых
величин, с помощью которых достигается сопоставимость разнородных единиц в
сложных статистических совокупностях.
Слайд 22
Основные категории индексного отношения:
Свойства соизмерителей:
необходимы для перехода от
натуральных измерителей разнородных единиц статистической совокупности к однородным показателям;
остаются
постоянными величинами при изменении индексируемой величины в числителе и знаменателе общего индекса.
Слайд 23
Соизмерители индексируемых величин -
экономические показатели:
цена (p);
количество (физический объем)
(g);
трудоемкость (t);
себестоимость (z).
Произведение каждой индексируемой величины на соизмеритель образует
в индексном отношении определенные экономические категории.
Слайд 24
Классификация индексов
Агрегатный индекс – сложный относительный показатель, который
характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов.
Отличительная
особенность агрегатного индекса – в числителе и знаменателе дроби участвует сумма показателей.
Слайд 25
Виды агрегатных индексов:
Индекс Пааше – характеризует влияние изменения
цен на стоимость товаров, реализованных в отчетном периоде, и
показывает насколько товары в текущем периоде стали дороже (дешевле) по сравнению с базисным.
Слайд 26
Виды агрегатных индексов:
Индекс Ласпейреса –характеризует влияние изменения цен
на стоимость количества товаров, реализованных в базисном периоде, и
показывает, во сколько раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетный период.
Слайд 27
3.Расчет статистических индексов
Расчет индивидуальных индексов:
цен: Jp =
p1 / p0 ;
физического объема: Jg= g1 /
g0;себестоимости: Jz=z1 / z0 ;
трудоемкости: Jt = t1 / t0.
Слайд 28
Расчет индексов:
Расчет индекса товарооборота:
p1 g1
х 100 %Jpg = p0 g0 , где
P1 – цена за единицу продукта в отчетном периоде;
P0 – цена за единицу продукта в базисном периоде;
g1- количество проданного товара в отчетном периоде;
g0 - количество проданного товара в базисном периоде.
Слайд 29
Расчет агрегатных индексов:
Индекс Пааше:
∑p1
g1Jp = ∑p0 g1 .
Индекс Ласпейреса:
∑p1 g0
Jp = ∑p0 g0 .
Слайд 30
Пример расчета статистических индексов.
Индексный факторный анализ
Имеются следующие
данные о ценах внешней торговли на некоторые виды товаров,
а также объеме их экспорта:
Слайд 32
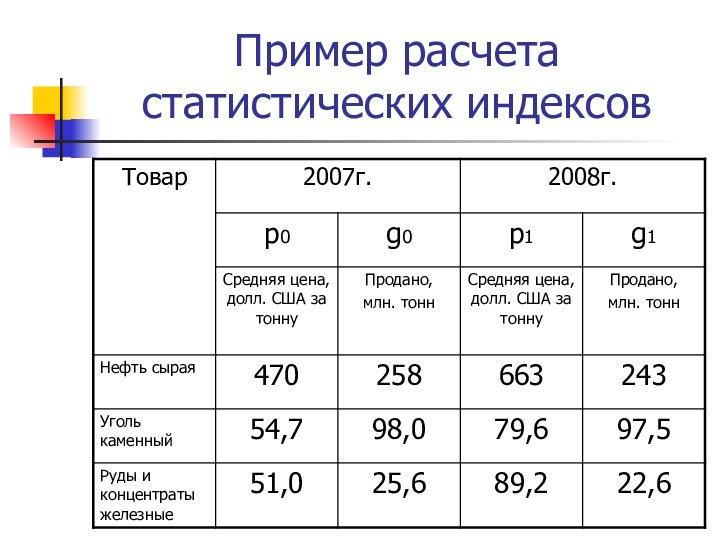
Пример расчета статистических индексов
Задание :
Определить динамику цен, объемов
продажи, стоимости проданных товаров, рассчитав:
Индивидуальные индексы цен, физического объема,
товарооборота каждого вида товаров;Агрегатные индексы товарооборота, цен, физического объема трех видов товаров;
Абсолютное изменение объема товарооборота за счет влияния факторов цены и количества проданных товаров.
Слайд 33
Пример расчета статистических индексов
1. Индивидуальные индексы цен рассчитываются
по формуле:
Jpi =p1 х 100 %.p0
Слайд 34
Расчет индивидуальных индексов цен
Jpн = (663/ 470) х
100 % = 141,1%
Jpу =(79,6/54,7) х 100 % =
145,5 %Jpр.к. =(89,2/51,0) х 100 % = 174,9%
Слайд 35
Пример расчета статистических индексов
2. Индивидуальные индексы физического объема
рассчитываются по формуле:
Jgi
= g1 • 100 %g0
Слайд 36
Расчет индивидуальных индексов физического объема:
Jgн =(243/258) х 100
% = 94,2%
Jgу = (97,5/98,0) х 100 % =
99,5%Jgр.к.= (22,6/25,6) х 100% = 88,3 %
Слайд 37
Пример расчета статистических индексов
3. Индивидуальные индексы товарооборота (стоимости
проданных товаров) рассчитываются по формуле:
p1 g1 х 100 %Jpg = p0 g0
Слайд 38
Расчет индивидуальных индексов товарооборота:
( 663 х 243) х 100%
Jpgн
= (470 х 258) = 132,9%(79,6х 97,5) х 100%
Jpgу = (54,7х98,0) =144,8%
(89,2х22,6) х 100%
Jpgр.к. = (51,0х25,6) =154,4%
Слайд 39
Пример расчета статистических индексов
1.Агрегатный индекс объема товарооборота рассчитывается
по формуле:
∑p1 g1 х 100%J ∑pg = ∑p0 g0
Слайд 40
Расчет агрегатного индекса товарооборота:
∑p1 g1 х
100%J ∑pg = ∑p0 g0 =
= 663 х 243 + 79,6 х 97,5 + 89,2 х 22,6 х 100%=
470 х 258 + 54,7 х 98,0 + 51,0 х 25,6
170885,92 х 100% = 90,93%
= 187922
Слайд 41
Расчет агрегатного индекса товарооборота:
Абсолютное изменение товарооборота в 2008г.
по сравнению с 2007г. рассчитывается по формуле:
∑p1 g1 -
∑p0 g0 = 170885,92 – 187922 = = - 17036,08 млн. долл. США
Таким образом, товарооборот уменьшился на 9,07% или на 17036,08 млн. долл. США.
Слайд 42
Пример расчета статистических индексов
2. Агрегатный индекс цен рассчитывается
по формуле:
∑p1 g1 х 100%J ∑p = ∑p0 g1
Слайд 43
Расчет агрегатного индекса цен:
∑p1 g1 х 100% =
J ∑p = ∑p0 g1
= 170885,92 х 100%=
470 х 243 + 54,7 х 97,5 + 51,0 х 22,6
= 170885,92 х 100% = 141,58 %
120695,85
Слайд 44
Расчет агрегатного индекса цен:
Абсолютное изменение товарооборота в 2008г.
по сравнению с 2007г. за счет изменения цен рассчитывается
по формуле:∑p1 g1 - ∑p0 g1 = 170885,92 – 120695,85 =
= 50190,07 млн. долл. США
Таким образом, за счет роста цен на 41,58% товарооборот возрос на 50190,07 млн. долл. США.
Слайд 45
Пример расчета статистических индексов
3. Агрегатный индекс физического объема
товарооборота рассчитывается по формуле:
∑p0 g1 х 100%J ∑g = ∑p0 g0
Слайд 46
Расчет агрегатного индекса физического объема:
∑p0 g1
х 100% =J ∑g = ∑p0 g0
= 120695,85 х 100% = 64,22%
187922
Слайд 47
Расчет агрегатного индекса физического объема:
Абсолютное изменение товарооборота в
2008г. по сравнению с 2007г. за счет изменения количества
проданных товаров рассчитывается по формуле:∑p0 g1 - ∑p0 g0 = 120695,85 – 187922 =
= - 67226,15 млн. долл. США
Таким образом, за счет уменьшения объема продажи товаров на 35,78 % товарооборот уменьшился на 67226,15 млн. долл. США.





























