Презентация на тему Показательные уравнения и неравенства

уравнений и неравенств
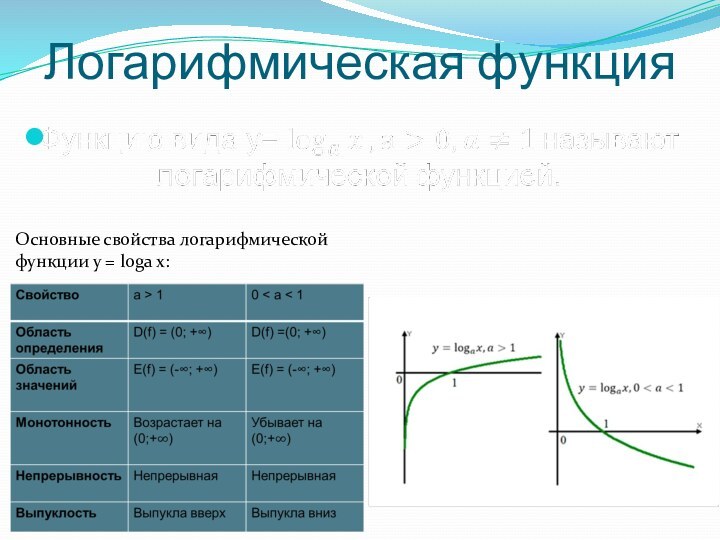
Логарифмических уравнений их функция
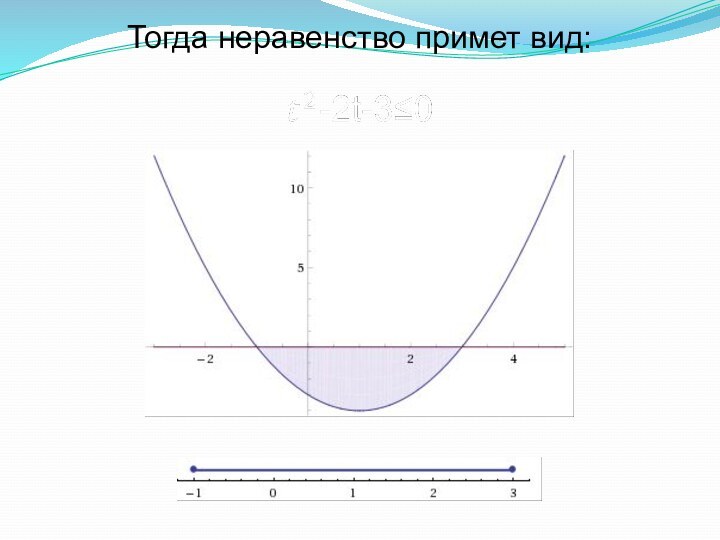
Логарифмические неравенства
Способы решения логарифмических

уравнений и неравенств
Примеры для самостоятельного решения

где a > 0 и a ≠ 1, называют

показательной функцией.

Основные свойства показательной функции y = ax:

находится только в показателях каких-либо степеней.
Для решения показательных уравнений

требуется знать и уметь использовать следующую несложную теорему:
Показательное уравнение af(x) = ag(x) (где a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).

и аналитические.
1. Построить графики двух функций (левая и правая части

уравнения);
2. Найти абсциссы точек пересечения графиков;
3. Записать ответ.
Рассмотрим графический способ решения на примере уравнения 2x = 4 Построим графики функций y = 2x, y = 4 и найдем абсциссу точки пересечения графиков: x = 2.








Ответ: x = 2

содержится только в показателях каких-либо степеней.
Для решения показательных неравенств

требуется знание следующей теоремы:

Если a > 1, то неравенство af(x) > ag(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 < a < 1, то показательное неравенство af(x) > ag(x) равносильно неравенству противоположного смысла: f(x) < g(x).

те же приемы, что при решении показательных уравнений.
Будьте внимательны:

показательная функция в зависимости от основания может быть возрастающей (а>1) или убывающей (а>1)
Пример:
Неравенства, сводящиеся к простейшим. Решаются приведением обеих частей неравенства к степени с одинаковым основанием.
а)2x2> 2 x+2.
Решение:
2x2> 2 x+2;
х2 > х+2, т.к. функция y =2t возрастает,
х2 – х–2 > 0;
x < – 1; x > 2.
Ответ:

x:

4. Логарифмирование обеих частей уравнения.
5. Приведение к одному основанию.
6.

Функционально-графический метод.

g(x) > 0, то:
при a > 1 логарифмическое неравенство

log a f(x) > log a g(x) равносильно неравенству того же смысла: f(x) > g(x);
при 0 < a < 1 логарифмическое неравенство log a f(x) > log a g(x) равносильно неравенству противоположного смысла: f(x) < g(x).