Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Интерполяция функций

Содержание

Интерполяция - это вычисление значений y (x) во всей области определения аргумента по заданному дискретному множеству точек, т.е. переход от дискретной функции к непрерывной.
Интерполяция функций Интерполяция - это вычисление значений y (x) во всей области определения аргумента  x0, x1,..., xn - узлы интерполяцииЗадача интерполирования: найти значение функции в точке xk, принадлежащей Линейная интерполяция.Линейная интерполяция - строится ломаная, которая проходит через точки (Xi;Yi), i=0,1,2,...,n, Параболическая интерполяцияПусть искомая функция полином:Потребуем, чтобы он проходил через заданные точки Составляем систему линейных уравнений и решаем ее любым методом: Интерполяционный полином ЛагранжаПолином степени N-1, проходящий через N точек.Требует большого объема вычислений.Если Интерполяция методом НьютонаПри равноотстоящих узлах метод Ньютона, более простой метод, нежели метод Лагранжа Вычисляем разности I-го порядка, через значение функции в соседних точках;Вычисляем разности II-го Интерполяционный полином n-й степени имеет вид Коэффициенты b определяются из условия: полином должен проходить через все заданные точки.Коэффициент Достоинства метода Ньютона: - более простые вычисления; - можно добавить
Слайды презентации

Слайд 2 Интерполяция - это вычисление значений y (x) во

Интерполяция - это вычисление значений y (x) во всей области определения

всей области определения аргумента по заданному дискретному множеству точек,

т.е. переход от дискретной функции к непрерывной.

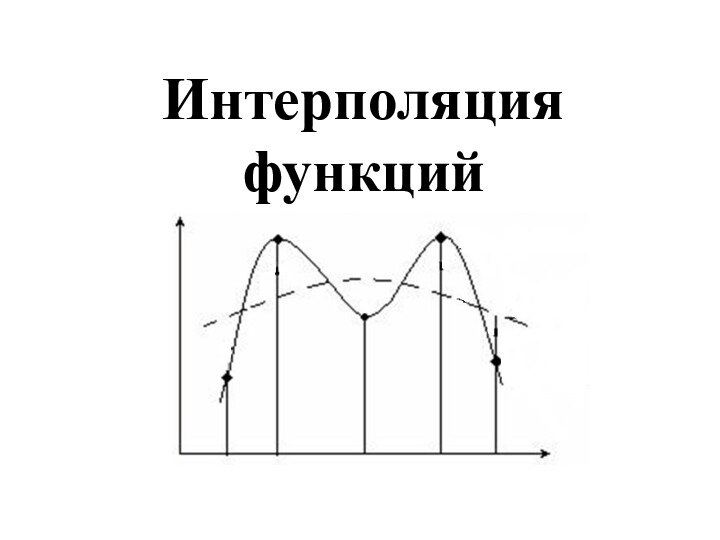
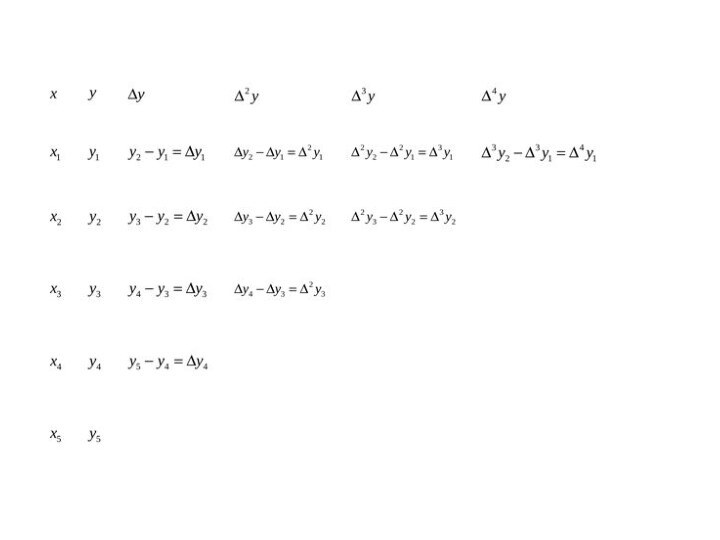
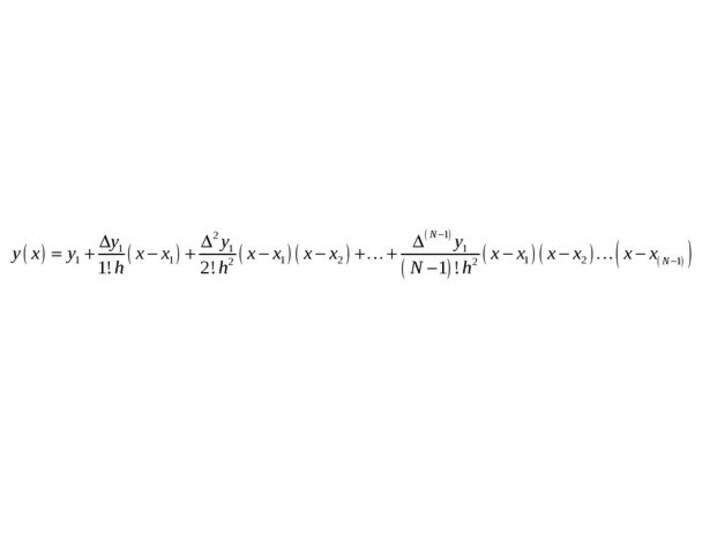
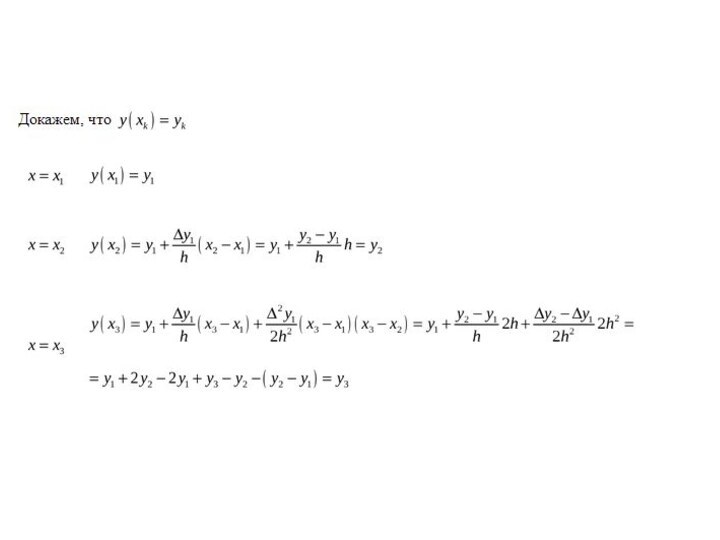
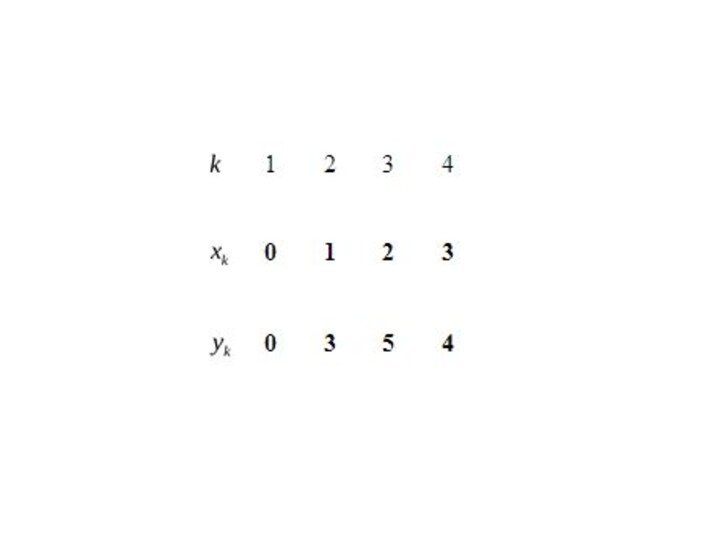
Слайд 3  x0, x1,..., xn - узлы интерполяции





Задача интерполирования: найти значение

 x0, x1,..., xn - узлы интерполяцииЗадача интерполирования: найти значение функции в точке xk,

функции в точке xk, принадлежащей отрезку [x0;xn], но при этом xk не

совпадает ни с одним узлом интерполяции (xk не равно x0, x1,...,xn.)

Слайд 4 Линейная интерполяция.

Линейная интерполяция - строится ломаная, которая проходит

Линейная интерполяция.Линейная интерполяция - строится ломаная, которая проходит через точки (Xi;Yi),

через точки (Xi;Yi), i=0,1,2,...,n, т.е. совпадающая с искомой функцией

в узлах интерполирования и линейная на каждом участке(Xi;Xi+1) при i=0,1,2,...,n-1.

Очевидно, что при Xi<=X<=Xi+1 значения функции будут вычисляться по формуле:
ϕ(X)=Yi+(X - Xi) (Yi+1 - Yi)/(Xi+1 - Xi).

Слайд 5 Параболическая интерполяция
Пусть искомая функция полином:


Потребуем, чтобы он проходил

Параболическая интерполяцияПусть искомая функция полином:Потребуем, чтобы он проходил через заданные точки

через заданные точки


Слайд 6

Слайд 7 Составляем систему линейных уравнений и решаем ее любым

Составляем систему линейных уравнений и решаем ее любым методом:

методом:

Слайд 8

Слайд 9

Слайд 10 Интерполяционный полином Лагранжа
Полином степени N-1, проходящий через N

Интерполяционный полином ЛагранжаПолином степени N-1, проходящий через N точек.Требует большого объема

точек.
Требует большого объема вычислений.
Если узлы полинома равноотстоящие – вычисления

упрощаются.
При изменении количества точек – полиномы L рассчитываются заново

Слайд 11

Слайд 12

Слайд 13 Интерполяция методом Ньютона
При равноотстоящих узлах метод Ньютона, более простой

Интерполяция методом НьютонаПри равноотстоящих узлах метод Ньютона, более простой метод, нежели метод Лагранжа

метод, нежели метод Лагранжа

Слайд 14 Вычисляем разности I-го порядка, через значение функции в

Вычисляем разности I-го порядка, через значение функции в соседних точках;Вычисляем разности

соседних точках;

Вычисляем разности II-го порядка, через разности первого порядка

в соседних точках;


Вычисляем разности n-ого порядка

Слайд 15

Слайд 16 Интерполяционный полином n-й степени имеет вид

Интерполяционный полином n-й степени имеет вид

Слайд 17 Коэффициенты b определяются из условия:
полином должен проходить

Коэффициенты b определяются из условия: полином должен проходить через все заданные

через все заданные точки.

Коэффициент b0 оцениваем через значение y(x1)

Коэффициент

b1 оцениваем через первую конечную разность Δy1


Коэффициент b2 оцениваем через вторую конечную разность Δy2




 

Слайд 18

Слайд 19

Слайд 20 Достоинства метода Ньютона: - более простые вычисления; - можно добавить

Достоинства метода Ньютона: - более простые вычисления; - можно добавить точки

точки и уточнить интерполяционный полином, не меняя предыдущих вычислений. 

  • Имя файла: interpolyatsiya-funktsiy.pptx
  • Количество просмотров: 116
  • Количество скачиваний: 1
- Предыдущая Математика в жизни человека
Следующая - Організація баз даних та знань. Системи баз даних. Основні поняття й архітектур. Основні поняття баз даних

Похожие презентации

Устный счет: сложение и вычитание Устный счет: сложение и вычитание 133
устный счёт 1-2 класс презентация к уроку по математике (1, 2 класс) устный счёт 1-2 класс презентация к уроку по математике (1, 2 класс) 113
Презентация урока по теме Координатная плоскость Презентация урока по теме Координатная плоскость 111
Конспект урока математики 3 класс Измерение ёмкости (УМК Планета знаний) план-конспект урока по математике (3 класс) Конспект урока математики 3 класс Измерение ёмкости (УМК Планета знаний) план-конспект урока по математике (3 класс) 134
Владимир Модестович Брадис Владимир Модестович Брадис 108
График функции и его перемещение в координатной плоскости График функции и его перемещение в координатной плоскости 97
Урок математики :Правильные и неправильные дроби план-конспект урока по математике (4 класс) Урок математики :Правильные и неправильные дроби план-конспект урока по математике (4 класс) 174
Формирование коммуникативной компетенции у младших школьников ( анализ учебника Математика 1 класса Н.Б. Истомина) статья по математике (1 класс) по теме Формирование коммуникативной компетенции у младших школьников ( анализ учебника Математика 1 класса Н.Б. Истомина) статья по математике (1 класс) по теме 125
Презентация для урока математики Решение простых задач на увеличение и уменьшение числа на несколько единиц, 1 класс презентация к уроку по математике (1 класс) Презентация для урока математики Решение простых задач на увеличение и уменьшение числа на несколько единиц, 1 класс презентация к уроку по математике (1 класс) 119
Арифметическая прогрессия в древности Арифметическая прогрессия в древности 129
ПРЕЗЕНТАЦИЯ ПО МАТЕМАТИКИ ПО ТЕМЕ Простые и составные числа ПРЕЗЕНТАЦИЯ ПО МАТЕМАТИКИ ПО ТЕМЕ Простые и составные числа 148
Фигуры Фигуры 106
Презентация по математике на тему Уравнение(5 класс) Презентация по математике на тему Уравнение(5 класс) 99
Презентация по математике на тему: Площадь прямоугольника и площадь квадрата Презентация по математике на тему: Площадь прямоугольника и площадь квадрата 123
Устный счёт до 20 Устный счёт до 20 149
Дидактическая игра Собери поезд методическая разработка по математике (младшая группа) Дидактическая игра Собери поезд методическая разработка по математике (младшая группа) 137
Решение иррациональных уравнений Решение иррациональных уравнений 124
Презентация по математике на тему Задачи на проценты. Презентация по математике на тему Задачи на проценты. 151
меры длины меры длины 110
Веселый счет Веселый счет 122
Конспект урока русского языка в 3 классе план-конспект урока по математике Конспект урока русского языка в 3 классе план-конспект урока по математике 102
Математика әлеміне саяхат Математика әлеміне саяхат 137
Презентация по математике на тему Деление суммы на число Презентация по математике на тему Деление суммы на число 125
Леонтий Филиппович Магницкий Леонтий Филиппович Магницкий 149
Играем в прятки с овощами Играем в прятки с овощами 106
Распределительное свойство умножения Распределительное свойство умножения 98
Умножение многочленов Умножение многочленов 102
Сфера и шар Сфера и шар 163
Четырёхзначные числа Четырёхзначные числа 108
pryamaya luch otrezok pryamaya luch otrezok 105