Презентация на тему Математическое моделирование

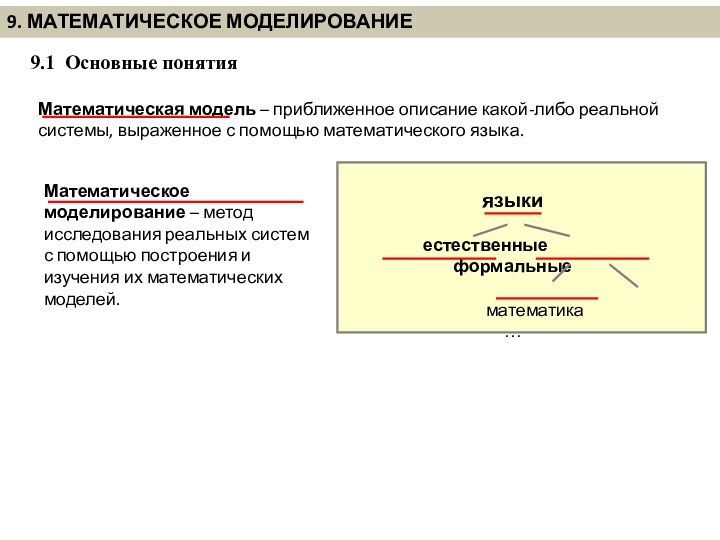
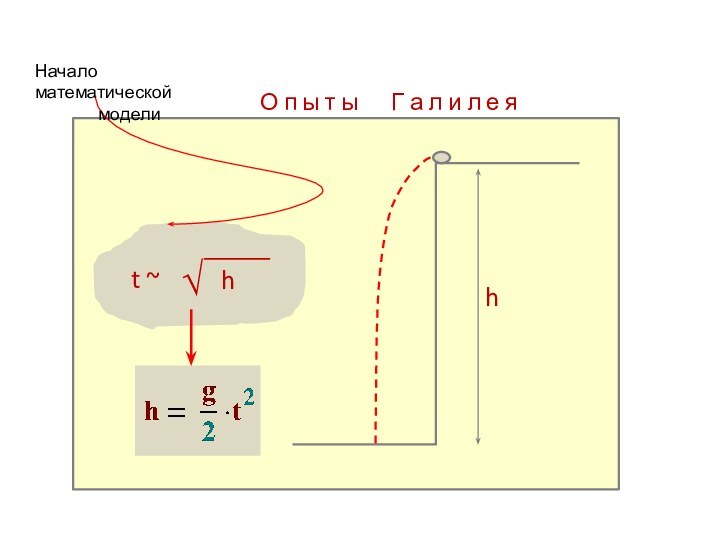
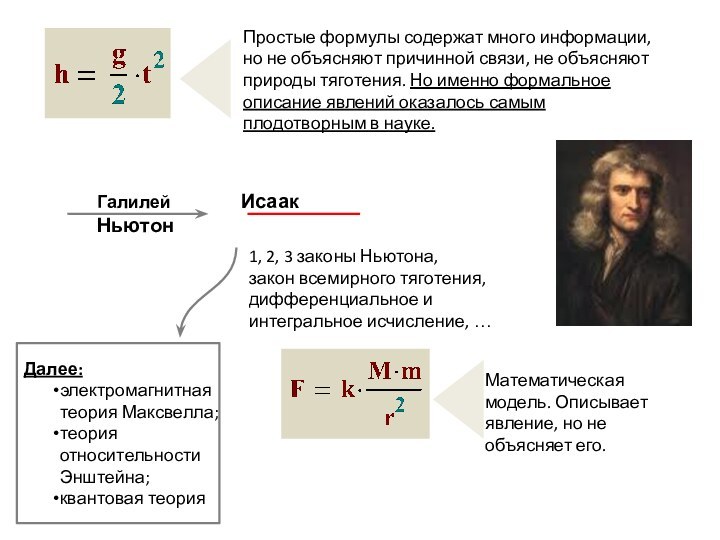
Египет), но широко – со времен Галилея.

До Галилея в

науке господствовал подход Аристотеля. Например:
В основе всего лежат 4 элемента (сущности):
Земля;
Огонь;
Воздух;
Вода.

Их свойства присущи всем вещам. Под действием притяжения (любовь) и отталкивания (ненависть) сущности могут комбинироваться. Такими комбинациями объясняются все явления в мире.
(ср. с китайским Янь-Инь)

А р и с т о т е л ь

картина мироздания. Для хорошего согласования с экспериментом модель Птолемея

была сильно усложнена – 77 кругов, эпициклы, деференты, …
Господствовала в науке около 1.5 тыс. лет – до Коперника, который взялся ее упростить.

Флоренция
Дата смерти:
8 января 1642 (77 лет)
Научная сфера:
философ,

физик, астроном,
математик

Начиная с XVII в. математическое моделирование занимает главенствующее положение в науке. Основоположники – Рене Декарт и Галилео Галилей.

Галилео Галилей.
При сотворении мира Бог вложил в него строгую математическую необходимость. Поэтому математическое знание не только истинно, но и священно.

Методология Галилея.
Камень падает вниз. Почему? – есть множество гипотез.
Но не следует путаться в этих объяснениях, а проводить, где это возможно, количественные описания.

Физические знания следует отделять от причинности!

а л и л е я
Начало математической
модели

причинной связи, не объясняют природы тяготения. Но именно формальное

описание явлений оказалось самым плодотворным в науке.

Галилей Исаак Ньютон

1, 2, 3 законы Ньютона,
закон всемирного тяготения, дифференциальное и интегральное исчисление, …

Математическая модель. Описывает явление, но не объясняет его.

Далее:
электромагнитная теория Максвелла;
теория относительности Энштейна;
квантовая теория

анализа исследуемого явления или объекта.
По результатам предварительных оценок, экспериментов,

интуитивных предположений все факторы, влияющие на реальную систему, делятся на две группы:
существенные;
несущественные.

Несущественными факторами пренебрегаем. Одновременно формулируются допущения, которые определяют границы применимости модели.

(на математическом языке). Обычно это алгебраические, дифференциальные или интегральные

уравнения.

Сколько можно
построить
математических
моделей

?

Много. Например, различной степени сложности.

Проблема выбора модели:

Слишком простые и слишком сложные модели на практике бесполезны!

?

модели Птолемея-Коперника

допущения)
математическая модель
решение математической модели
анализ результатов
оценка адекватности
да
н е т
комп.моделирование
разработка численного

алгоритма;

компьютерная программа;

отладка и тестирование программы;

расчет на компьютере

метода. Для этого проводится расчет некоторых вариантов задачи, для

которых имеются известные аналитические решения или надежные экспериментальные данные.

Например,

- аналитического решения нет

Тестовые варианты:
а)


б)

есть аналитические
решения

Оценка адекватности. Полученные результаты обрабатываются и анализируются. После этого делаются выводы:
математическая модель удовлетворяет поставленным требованиям;
модель требует уточнений – модифицируется (как правило, усложняется) и проводится новый цикл исследования.

– N жителей. В некоторый момент времени t0 автобусом

(поездом, самолетом, пешком,...) прибыло x0 больных свиным гриппом. Построить модель распространения эпидемии и провести ее исследование.

Основные допущения:
иммунитета к болезни нет;
летальных исходов нет;
больные равномерно распределены среди здоровых;
у всех болезнь протекает одинаково.

больные

N жителей

x0

Математическая модель

Введем обозначения: x – количество больных, t – время.

Тогда количество вновь заболевших (скорость распространения

эпидемии) будет .

справедливы:

1) 

2) 

(1)

количество
здоровых

Здесь k – некоторый коэффициент
(контактность)

Введем параметр

больных нет

все больны

(2)

(задача Коши)

безразмерным переменным. Для этого введем некоторые характерные значения (масштабы)

: t* - для времени, x * - для количества больных.

В нашей задаче можно выбрать x *= N, t* = 1/kN.

Тогда задача (2) в безразмерной форме будет

(3)

Здесь единственный параметр

в начальный момент больных нет;

все уже больны.

предельные
значения

 = 0   0 ,

 = 1   1

Рассмотрим два частных случая:

MC: Demo
Мат Моделирование

MC: Demo
Мат Моделирование

модели) эпидемия затухает на бесконечности.
А как практически?
Когда можно

считать, что эпидемия пошла на спад?