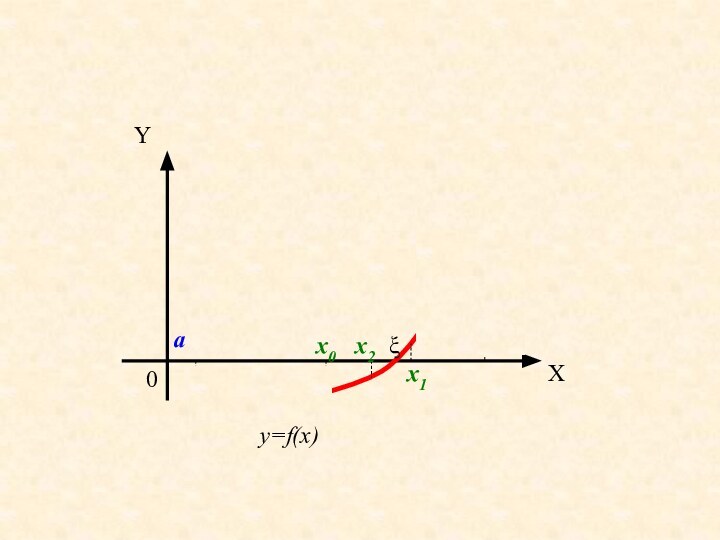
f (x)=0
(1)Задача нахождения корней уравнения (1) обычно решается в два этапа.
На первом этапе изучается расположение корней и проводится их разделение, то есть выделяются области, содержащие только один корень.
На втором этапе, используя начальное приближение, строится итерационный процесс для уточнений корня.


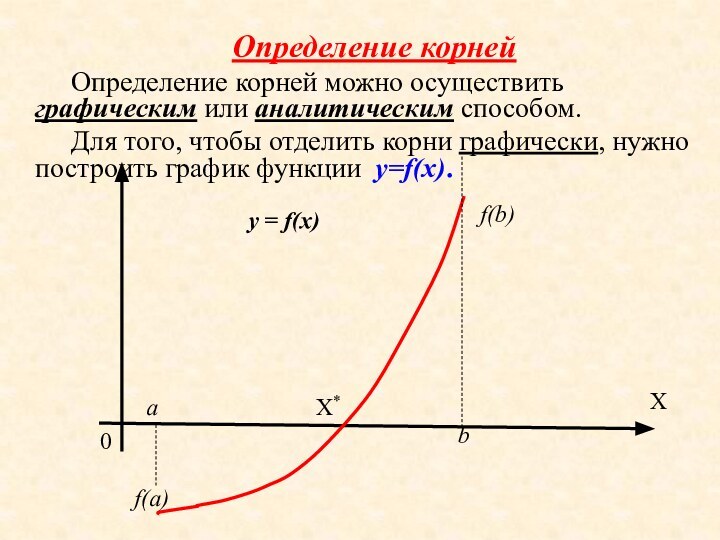

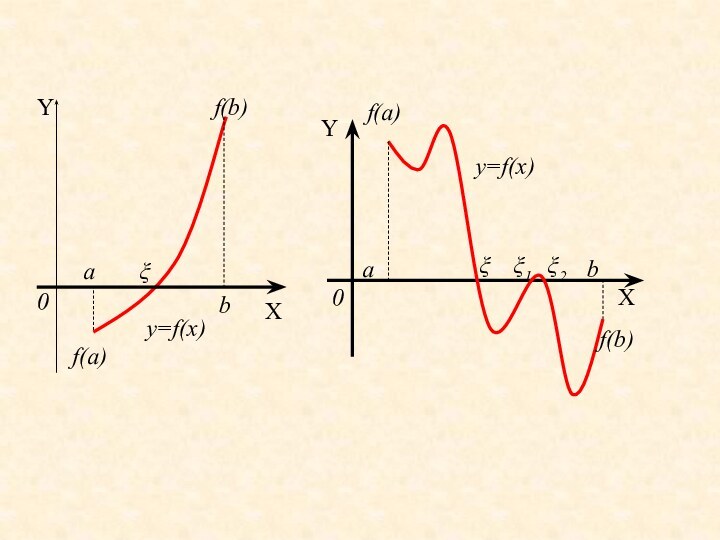
![Исследование математических моделей Метод половинного деления Предположим что в интервале [a, b] расположен один](/img/tmb/14/1301673/cea92c7609fb141e44e2af6af051a524-720x.jpg)