- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория вероятностей
Содержание
- 2. Вероятность события В различных областях
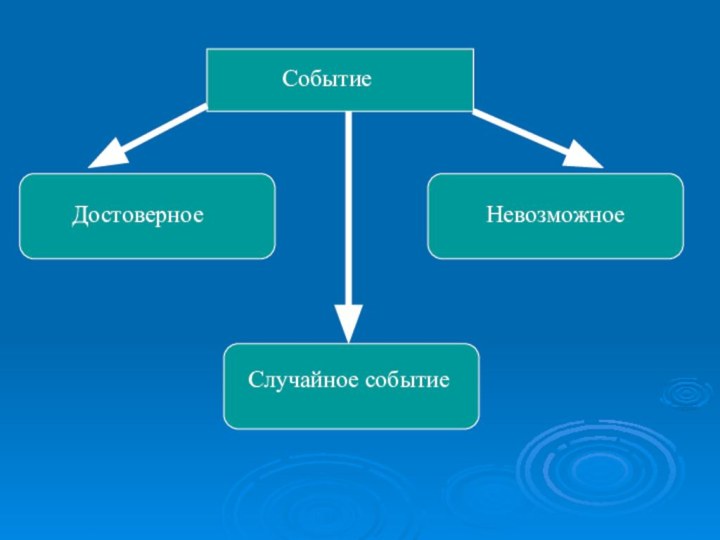
- 3. СобытиеДостоверноеСлучайное событиеНевозможное
- 4. Определения: Случайным называется событие, которое может произойти или
- 5. Пример:
- 6. Определение: Достоверным называется событие, обязательно появляющееся в результате
- 7. Определение: Невозможным называется событие, которое не может произойти
- 8. Совместные и несовместные событияСобытияСовместныеНесовместныеНесколько событий называются совместными,
- 9. Пример совместных событий Событие А –
- 10. Пример несовместных событий Событие А –
- 11. ОПРЕДЕЛЕНИЕ События называются единственно возможными,
- 12. Равновозможные событияОпределение Несколько событий называются равновозможными, если в
- 13. Полная группа событий. Противоположные событияОпределения События образуют полную группу
- 14. Алгебра событий Суммой событий
- 15. Вероятность события Вероятность является количественной мерой возможности появления
- 16. Пример Рассматриваемое событие А – четное число очков
- 17. Вероятность события Относительной частотой появления события А называется
- 18. Статистическое определение вероятности события При очень большом числе
- 19. Свойства вероятности 1. Вероятность достоверного события равна 1. 2.
- 20. Пример Структура занятых в региональном отделении крупного банка
- 21. Решение а) Событие А – случайно выбранный
- 22. Решение б) Событие В – случайно выбранный
- 23. Решение в) Событие С – случайно выбранный
- 24. Теорема сложения вероятностей несовместных событий Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий
- 25. Условная вероятностьОпределение Вероятность события А, вычисленная при условии,
- 26. Теорема умножения вероятностей Вероятность произведения двух событий равна
- 27. Независимые и зависимые событияОпределение События А и В
- 28. Теорема сложения вероятностей совместных событий Вероятность суммы двух
- 29. Вероятность появления хотя бы одного события Если события
- 30. Пример Студент пришел на экзамен, выучив 15 вопросов
- 31. Скачать презентацию
- 32. Похожие презентации
Вероятность события В различных областях человеческой деятельности приходится иметь дело с событиями, которые невозможно точно предсказать. Поэтому приходится прогнозировать исход такой деятельности на основе собственного или чужого опыта, либо на основе интуиции, опирающейся на опытные




























Слайд 2
Вероятность события
В различных областях человеческой деятельности
приходится иметь дело с событиями, которые невозможно точно предсказать.
приходится прогнозировать исход такой деятельности на основе собственного или чужого опыта, либо на основе интуиции, опирающейся на опытные данные.
Слайд 4
Определения:
Случайным называется событие, которое может произойти или не
произойти в результате некоторого испытания
Испытание (опыт, эксперимент) – это
процесс, включающий определенные условия и приводящий к одному из нескольких возможных исходов.Исходом испытания может быть результат наблюдения или измерения.
Единичный, отдельный исход испытания называется элементарным событием
Слайд 6
Определение:
Достоверным называется событие, обязательно появляющееся в результате опыта.
Достоверные события обозначаются
символом -
Пример:Извлечение из урны, содержащей только белые шары, белого шара.
Слайд 7
Определение:
Невозможным называется событие, которое не может произойти в
результате опыта.
Невозможные события обозначаются
символом
- Пример:
Извлечение из урны, содержащей только белые шары, черного шара.
Достоверные и невозможные события не являются случайными.
Слайд 8
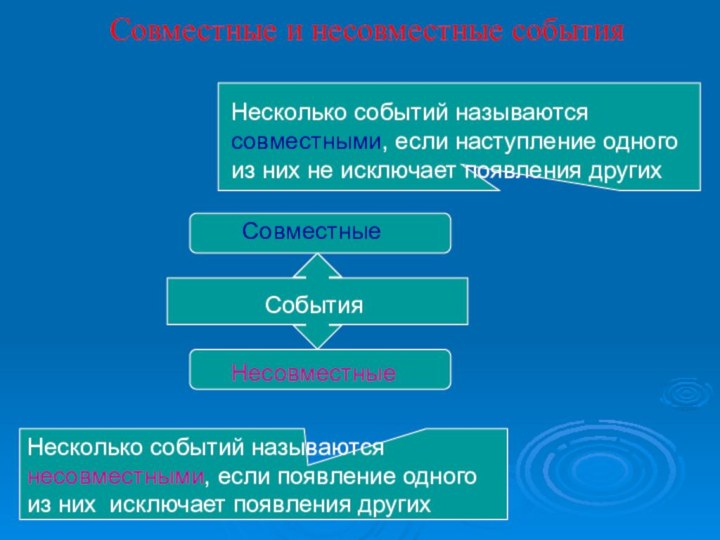
Совместные и несовместные события
События
Совместные
Несовместные
Несколько событий называются совместными, если
наступление одного из них не исключает появления других
Несколько событий
называются несовместными, если появление одного из них исключает появления других
Слайд 9
Пример совместных событий
Событие А – в
магазин вошел покупатель старше 60 лет
Событие В
– в магазин вошла женщинаСобытия А и В совместны, так как в магазин может войти женщина старше 60 лет
Слайд 10
Пример несовместных событий
Событие А – выигрыш
одной партии в шахматы
Событие В – проигрыш
одной партии в шахматыСобытие С – ничейный исход одной партии в шахматы
События А , В и С несовместны
Слайд 11
ОПРЕДЕЛЕНИЕ
События называются единственно возможными, если
в результате испытания хотя бы одно из них произойдет
ПРИМЕР
Фирма
рекламирует свой товар по радио и в газете.Единственно возможные события:
Потребитель услышит о товаре по радио;
Потребитель прочитает о товаре в газете;
Потребитель получит информацию о товаре по радио и в газете;
Потребитель не слышал о товаре по радио и не читал в газете.
Слайд 12
Равновозможные события
Определение
Несколько событий называются равновозможными, если в результате
испытания ни одно из них не имеет объективно большую
возможность появления, чем другие.Пример
При бросании игральной кости появление каждой из ее граней – события равновозможные.
Слайд 13
Полная группа событий. Противоположные события
Определения
События
образуют полную группу событий,
если хотя бы одно из них обязательно произойдет в
опыте.Два единственно возможных события, образующих полную группу, называются противоположными
Пример:
А
А
А – событие
А – противоположное событие
Полная группа событий
Слайд 14
Алгебра событий
Суммой событий
называется событие, состоящее в появлении хотя бы одного из этих событий
Произведением событий называется событие, состоящее в одновременном появлении всех этих событий
Слайд 15
Вероятность события
Вероятность является количественной мерой возможности появления события
Классическое
определение
Вероятностью события А называют отношение числа благоприятствующих элементарных исходов
(m ) к общему числу равновозможных элементарных исходов, образующих полную группу (n).
Слайд 16
Пример
Рассматриваемое событие А – четное число очков на
выпавшей грани игральной кости
Общее число исходов (число граней) –
6Число благоприятствующих исходов (грани содержащие 2,4,6 очков) – 3
..
.
Слайд 17
Вероятность события
Относительной частотой появления события А называется отношение
числа испытаний m1, при которых событие появилось, к общему
числу произведенных испытаний n1.Статистическое определение
Вероятностью события А называется число, относительно которого устанавливается относительная частота W(A) при неограниченном увеличении числа опытов
Слайд 18
Статистическое определение вероятности события
При очень большом числе испытаний
статистическая вероятность приближенно равна классической.
В практических задачах за вероятность
события принимается относительная частота при достаточно большом числе испытаний.
Слайд 19
Свойства вероятности
1. Вероятность достоверного события равна 1.
2. Вероятность
невозможного события равна 0.
3. Вероятность случайного события есть положительное
число, заключенное между 0 и 1.4. Сумма вероятностей противоположных событий равна 1.
Слайд 20
Пример
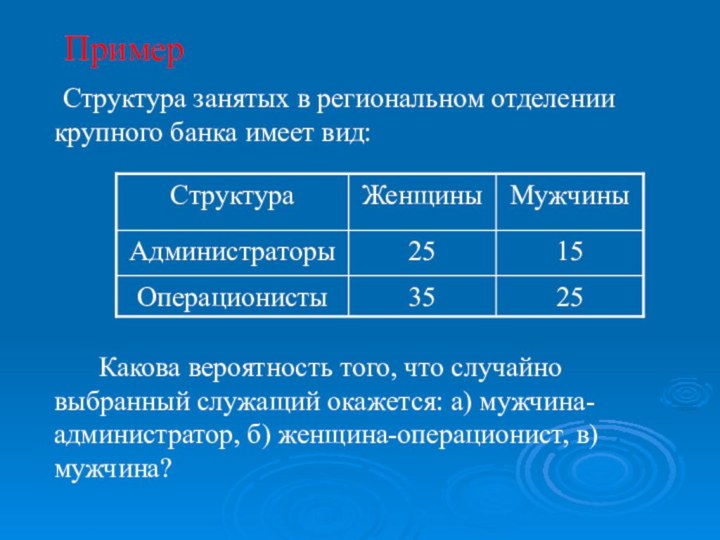
Структура занятых в региональном отделении крупного банка имеет
вид:
Какова вероятность того, что случайно выбранный служащий окажется: а)
мужчина-администратор, б) женщина-операционист, в)мужчина?
Слайд 21
Решение
а) Событие А – случайно выбранный служащий
– мужчина-администратор.
Вычислим вероятность события А, используя классическое определение вероятности:
Общее
число исходов это численность работающих в банке служащих n=100.Число благоприятствующих исходов это численность мужчин-администраторов m=15.
Тогда вероятность события А равна:
Слайд 22
Решение
б) Событие В – случайно выбранный служащий
– женщина-операционист.
Общее число исходов это численность работающих в банке
служащих n=100.Число благоприятствующих исходов это численность женщин-операционисток m=35.
Тогда вероятность события в равна:
Слайд 23
Решение
в) Событие С – случайно выбранный служащий
– мужчина.
Общее число исходов это численность работающих в банке
служащих n=100.Число благоприятствующих исходов это численность мужчин m=40.
Тогда вероятность события в равна:
Слайд 24
Теорема сложения вероятностей несовместных событий
Вероятность суммы конечного числа
несовместных событий
равна сумме вероятностей этих событий
Слайд 25
Условная вероятность
Определение
Вероятность события А, вычисленная при условии, что
имело место другое событие В, называется условной вероятностью события
АЕсли вероятность события А рассматривается при условии, что произошли два других события В и С, используется условная вероятность относительно произведения событий В и С
Слайд 26
Теорема умножения вероятностей
Вероятность произведения двух событий равна произведению
вероятности одного из них на условную вероятность другого, вычисленную
при условии, что первое имело местоПример: В магазине 35 компьютеров, 5 из них с дефектами. Найти вероятность того, два наугад взятых компьютера без дефектов.
Решение: А – первый наугад взятый компьютер без дефекта
В - второй наугад взятый компьютер без дефекта, при условии, что первый компьютер без дефекта
Слайд 27
Независимые и зависимые события
Определение
События А и В называются
независимыми, если при наступлении события А вероятность события В
не меняется.Для независимых событий
События А и В называются зависимыми, если вероятность каждого из них зависит от того произошло или нет другое событие.
Слайд 28
Теорема сложения вероятностей совместных событий
Вероятность суммы двух совместных
событий А и В равна сумме вероятностей этих событий
без вероятности их совместного наступления
Слайд 29
Вероятность появления хотя бы одного события
Если события
независимы в совокупности, тогда вероятность появления события А, состоящего в появлении хотя бы одного из событий равна:
Слайд 30
Пример
Студент пришел на экзамен, выучив 15 вопросов из
25. Экзаменатор задал студенту 3 вопроса. Какова вероятность того,
что студент ответит на все 3 вопроса?Решение:
Событие А – студент знает все 3 вопроса- заключается в совместном наступлении событий:
- студент знает 1-й вопрос;
- студент знает 2-й вопрос;
- студент знает 3-й вопрос.
События , , - зависимые