- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Комбинаторика и её применение
Содержание
- 2. Проблемный вопрос: Может ли нам комбинаторика помочь в реальной жизни?
- 3. Цель: продолжить знакомство с наукой комбинаторика
- 4. Гипотеза: Решение комбинаторных задач развивает творческие
- 5. Устный счет1. Сколько двузначных чисел можно составить,
- 6. 147 14, 17, 41,
- 7. Устный счет2. Сколько различных трехзначных чисел можно
- 8. 3 7 8 78 87 3
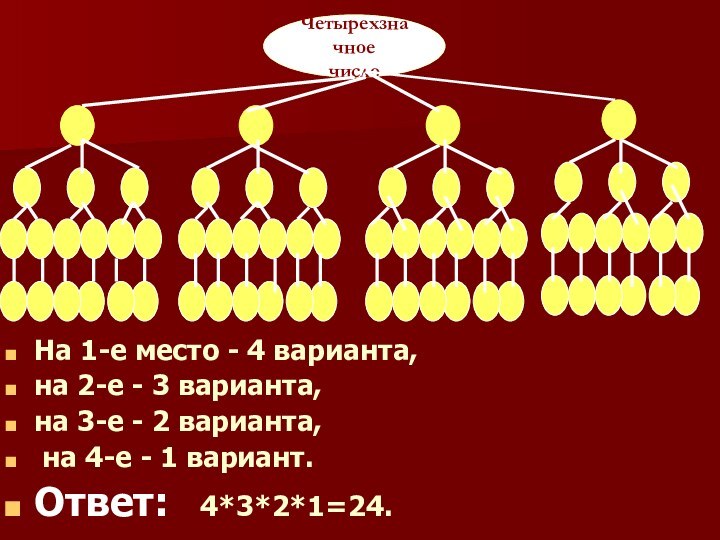
- 9. Устный счет3. Сколько четырехзначных чисел можно составить из 4 цифр?
- 10. На 1-е место - 4 варианта, на
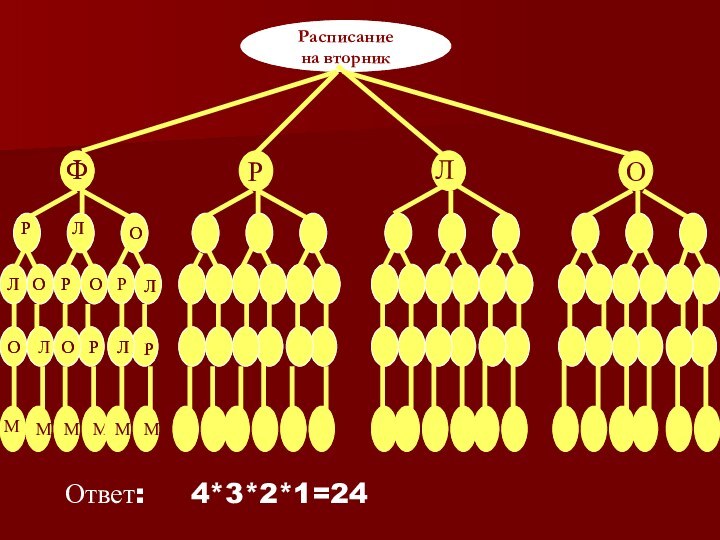
- 11. Задача № 1 В 6 классе во
- 12. ОРЛОРЛОММММММОтвет: 4*3*2*1=24Расписаниена вторник
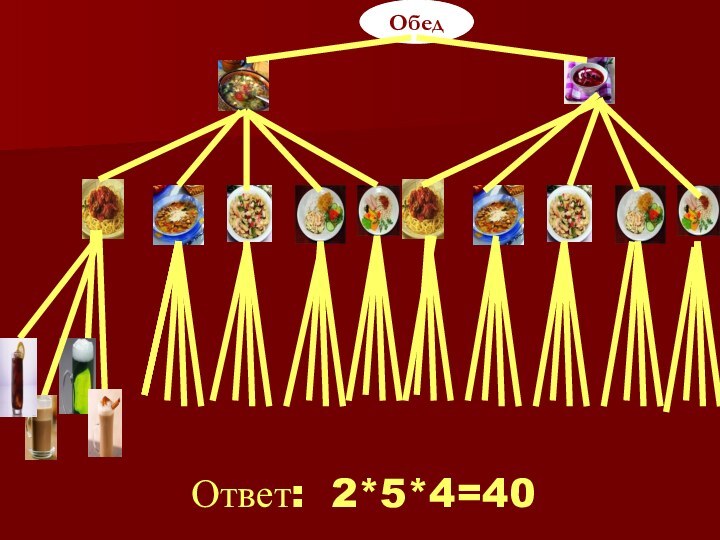
- 13. Задача № 2 В школьной
- 14. Ответ: 2*5*4=40Обед
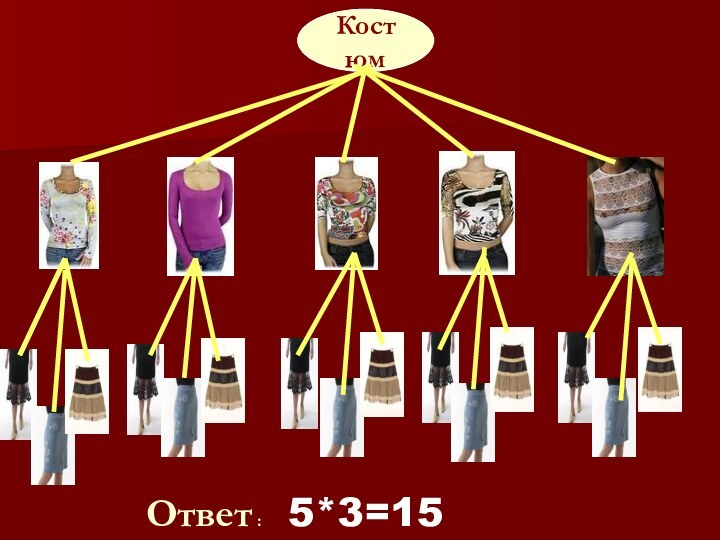
- 15. Задача № 3У Светланы 3 юбки и
- 16. Ответ : 5*3=15Костюм
- 17. Задача 4На полке лежат 3 книги. Сколькими способами можно расставить на полке эти книги ?
- 18. Решение Обозначим книги буквами А, В, С.
- 19. Опыт с листом бумаги Дима
- 20. Ответ
- 21. Самостоятельная работаВариант I В
- 22. Ответы самостоятельной работыВариант IРешение: Золотую медаль может
- 23. Области применения
- 24. Области применения
- 25. Вывод:Комбинаторика повсюду.Комбинаторика везде.Комбинаторика вокруг нас.
- 26. Без знания прошлого нет настоящего, нет
- 27. Домашнее задание:придумать свою комбинаторную задачу и решить
- 28. Скачать презентацию
- 29. Похожие презентации
Проблемный вопрос: Может ли нам комбинаторика помочь в реальной жизни?





















Слайд 3
Цель:
продолжить знакомство с наукой комбинаторика
Задача:
научиться находить все возможные комбинации для решения комбинаторных задач
Слайд 4
Гипотеза:
Решение комбинаторных задач развивает творческие способности,
помогает при решении олимпиадных задач, задач из ЕГЭ.
Слайд 5
Устный счет
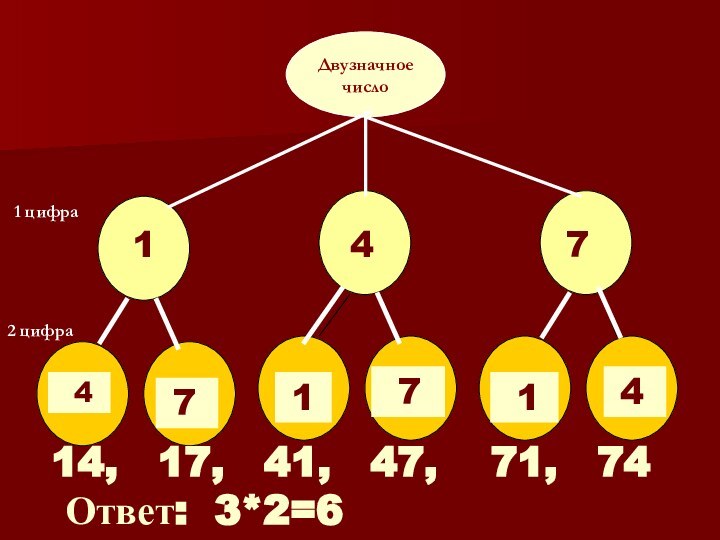
1. Сколько двузначных чисел можно составить, используя
цифры 1, 4 и 7 (цифры в числе не
повторяются)?
Слайд 7
Устный счет
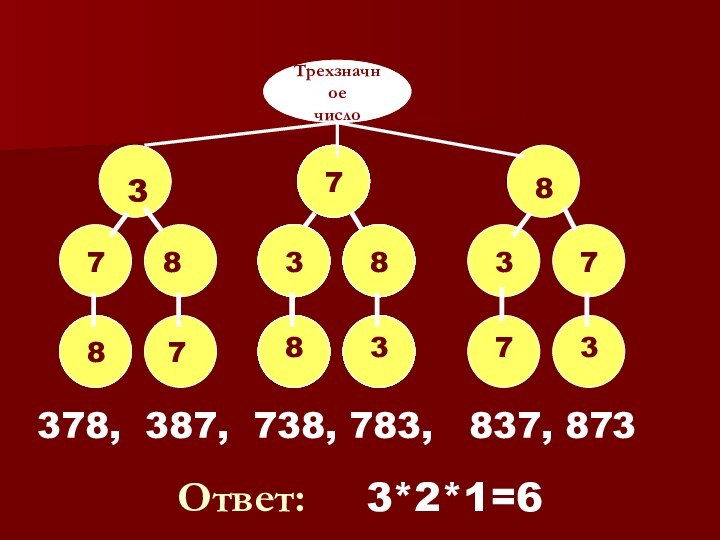
2. Сколько различных трехзначных чисел можно составить
из цифр 3, 7 и 8
(цифры не повторяются)?
Слайд 10
На 1-е место - 4 варианта,
на 2-е
- 3 варианта,
на 3-е - 2 варианта,
на
4-е - 1 вариант.Ответ: 4*3*2*1=24.
Четырехзначное
число
Слайд 11
Задача № 1
В 6 классе во вторник
5 уроков: физкультура, русский язык, литература, обществознание и математика.
Сколько можно составить вариантов расписания на день, зная точно, что математика – последний урок?
Слайд 13
Задача № 2
В школьной столовой
имеются 2 первых, 5 вторых и 4 третьих блюд.
Сколькими способами ученик может выбрать обед, состоящий из первых, вторых и третьих блюд?
Слайд 15
Задача № 3
У Светланы 3 юбки и 5
кофт, удачно сочетающихся по цвету. Сколько различных комбинаций одежды
имеется у Светланы?
Слайд 18
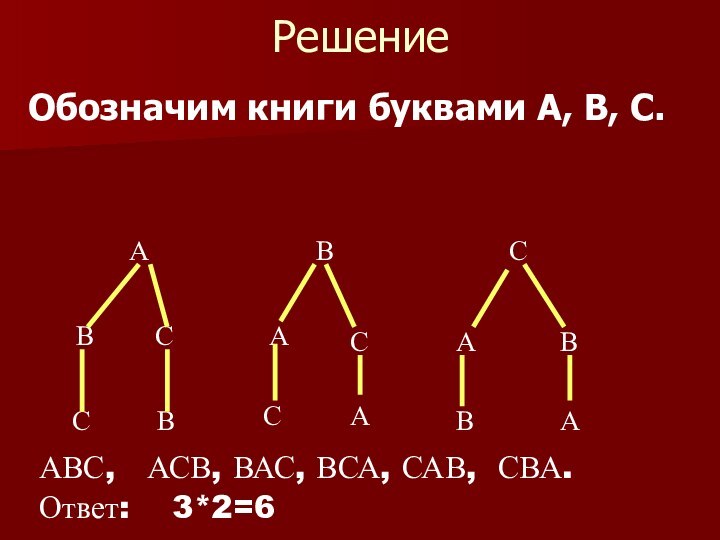
Решение
Обозначим книги буквами А, В, С.
А
В
С
В
С
А
С
А
В
АВС, АСВ, ВАС, ВСА,
САВ, СВА.Ответ: 3*2=6
С
В
С
А
В
А
Слайд 19
Опыт с листом бумаги
Дима сложил квадратный
листок бумаги пополам, потом еще раз и еще раз.
В центре того, что получилось, он проделал дырку, а потом снова развернул лист.Сколько дырок он увидел?
(A)2; (B) 3; (C) 4; (D) 6; (E) 8;
Слайд 20
Ответ
Каждое
складывание увеличивает толщину (в слоях) бумаги в два раза.
Дима складывал бумагу три раза и получил толщину 2 · 2 · 2 = 8.Дырки получатся на каждом листе. Итого 8 дырок.
Верен ответ (Е).
Слайд 21
Самостоятельная работа
Вариант I
В розыгрыше
первенства страны по футболу принимает участие 16 команд. Сколькими
способами могут быть распределены золотая и серебряная медали?Выберите букву правильного ответа.
А) 256 Б) 31
В) 240 Г) 16
Вариант II
В классе 25 учащихся, сколькими способами можно выбрать старосту класса и его заместителя?
Выберите букву правильного ответа.
А) 25 Б)600
В) 49 Г) 625
Слайд 22
Ответы самостоятельной работы
Вариант I
Решение: Золотую медаль может получить
одна из 16 команд. После того как определен владелец
золотой медали, серебряную медаль может иметь одна из 15 команд. Следовательно, общее число способов, которыми могут быть распределены золотая и серебряная медали, равно16 . 15 = 240.
Ответ: В
Вариант II
Решение: Староста класса может быть выбран 1 из 25 человек, значит существует 25 способов выбора старосты и 24 способа выбора его заместителя. Существует 25 . 24 = 600 способов выбора старосты класса и его заместителя.
Ответ : Б
Слайд 23 Области применения
комбинаторики:
учебные заведения ( составление расписаний)
сфера
общественного питания (составление меню)лингвистика (рассмотрение вариантов комбинаций букв)
спортивные соревнования (расчёт количества игр между участниками)
агротехника (размещение посевов на нескольких полях)
география (раскраска карт)
биология (расшифровка кода ДНК)
Слайд 24 Области применения
комбинаторики:
химия (анализ возможных связей между
химическими элементами)экономика (анализ вариантов купли-продажи акций) азартные игры (подсчёт частоты выигрышей)
криптография (разработка методов шифрования)
доставка почты (рассмотрение вариантов пересылки)
военное дело (расположение подразделений)