Презентация на тему Координатный метод в пространстве

проведены три попарно перпендикулярные прямые, на каждом из них

выбрано направление(оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
Рассмотрим рисунок

РИСУНОК
Прямые с выбранными на них направлениями

называются осями координат, а их общая точка – началом координат.
Плоскости, проходящие соответственно через оси координат Ох и Оy, Oу и Оz, Oz и Ox, называются координатными плоскостями и обозначаются Oxy, Oхz , Ozх.

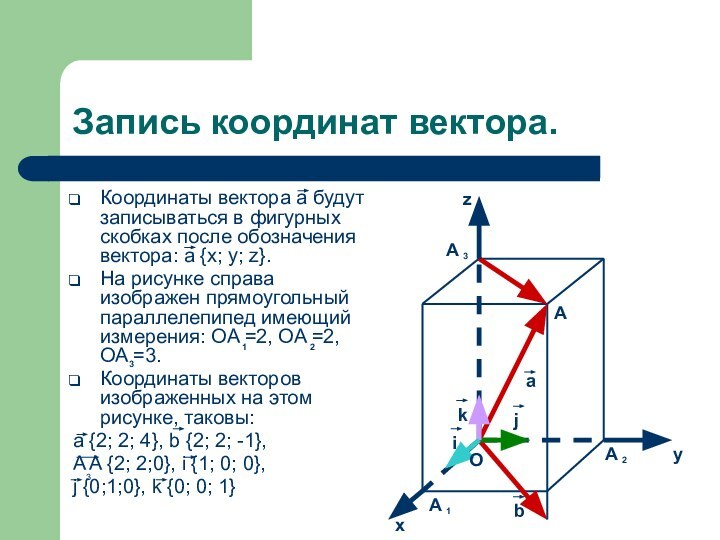
Ось Аппликат

Ось абсцисс

Ось ординат

y

z

O

x

из осей координат на два луча. Луч, направление которого

совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью.

M пространства сопоставляется тройка чисел, которые называются её координатами.
y
z
x
M
1
M
2
M
3
M
O

лежит на координатной плоскости или на оси координат, то

некоторые её координаты равны нулю. Так, если M принадлежит Oxy, то аппликата точка M равна нулю: z=0. Аналогично если M принадлежит Oхz, то y=0, а если M принадлежит Oyz, то x=0. Если M принадлежит Ox, то ордината и аппликата точки M равна нулю: y=0 и z=0. Если M принадлежит Oy, то x=0 и z=0; если M принадлежит Oz, то x=0 и y=0. Все три координаты начала координат равны нулю: О (0;0;0). Напиши координаты для точек A, B, C, D, E, F на рисунке следующего слайда.

4),
E(0; 5; 0),
F(0; 0; -2).
Сравни свои ответы.

начала координат единичный вектор, т.е. вектор, длина которого равна

единицы.

j

k

i

y

z

x

O

по координатным векторам, т.е. представить в виде

а = xi + yj + zk
Причем коэффициенты разложения x, y, z определяются единственным образом.

фигурных скобках после обозначения вектора: а {x; y; z}.

На рисунке справа изображен прямоугольный параллелепипед имеющий измерения: OA =2, OA =2, OA =3.
Координаты векторов изображенных на этом рисунке, таковы:
a {2; 2; 4}, b {2; 2; -1},
A A {2; 2;0}, i {1; 0; 0},
j {0;1;0}, k {0; 0; 1}

A

A

A

A

O

y

x

z

a

j

i

k

b

3

2

1

1

2

3

3

можно представить в виде 0 = 0i + 0j

+ 0k, то все координаты нулевого вектора равны нулю.
Координаты равных векторов соответственно равны, т.е. если векторы
a {x ; y ; z } и b {x ; y ; z } равны, то x =x , y =y и z =z .

1

1

1

2

2

2

1

2

1

2

1

2

число.
Каждая координата суммы двух или более векторов равна сумме

соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a + b имеет координаты
{x +x ; y +y ; z +z }

1

2

1

2

1

2

2

2

2

1

1

1

соответствующих координат этих векторов. Если a {x ; y

; z } и b {x ; y ; z } – данные векторы, то вектор a – b имеет координаты
{x –x ; y –y ; z –z }

1

2

1

2

1

2

1

2

1

1

2

2

произведение соответствующей координаты вектора на это число. Если a

{x; y; z } – данный вектор, α - данное число, то вектор αa имеет координаты
{ x; y; z}

α

α

α

которого совпадает с данной точкой, а начало – с

началом координат, называется радиус-вектором данной точки.
Координаты любой точки равны соответствующим координатам её радиус-вектора.
Каждая координата вектора равна разности соответствующих координат его конца и начала.

полусумме соответствующих координат его концов.
Длина вектора a {x; y;

z} вычисляется по формуле
|a| = √x² + y² + z²

y ; z ) и
M (x ; y

; z ) вычисляется по формуле

d = √(x – x )² + (y – y )² + (z – z )²

1

2

2

2

2

1

1

1

2

1

2

1

2

1

середины отрезков AC, OC и CB.
Найти по рисунку справа

координаты векторов AC, CB, AB.

P

B

y

N

j

i

k

M

O

C

A

x

z

2k, AC {-4; 0; 2}
CB = CO + OB

= 2k + 9j, CB {0; 9; 2}
AB = AO + OB = -4i + 9j, AB {-4; 7; 0}