Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Кривые второгопорядка

Содержание

2. Кривой второго порядка называется линия,
3. Окружность Окружностью называетсяся множество точек плоскости,
4. Эллипс Эллипсом называется геометрическое место точек
7. Уравнение эллипса
8. Эллипс
9. Оси симметрии эллипса называются его
10. Точки пересечения эллипса с осями
11. Отношение
12. Замечание Если
13. Гипербола Гиперболой называется геометрическое место точек,
14. XYYMУ
15. Уравнение гиперболы
16. Гипербола
17. Из уравнения гиперболы видно, что
18. Основной прямоугольник гиперболы Прямоугольник,
19. Для гиперболы Фокусы гиперболы :
20. Оси и полуоси гиперболы Принято говорить:
21. Асимптоты Гипербола имеет две асимптоты, т.
22. Отношение называется эксцентриситетом гиперболы
23. Замечание Для гиперболы
24. Парабола Параболой называется геометрическое место
25. Если расположить ось Ох перпендикулярно
26. Парабола
27. Фокус параболы -
28. Парабола
29. Фокус этой параболы
30. Самостоятельно изучить параболы
31. Общее уравнение кривой второго порядка
32. Пример Привести уравнение 2х²+3у²-16х-64=0 кривой второго
33. Для того чтобы привести уравнение
34. Это каноническое уравнение эллипса. Полуоси этого
35. Пример Составить каноническое уравнение гиперболы, зная,
36. Тогда малая полуось Уравнение гиперболы имеет вид
37. Пример Составить уравнение гиперболы, если расстояние
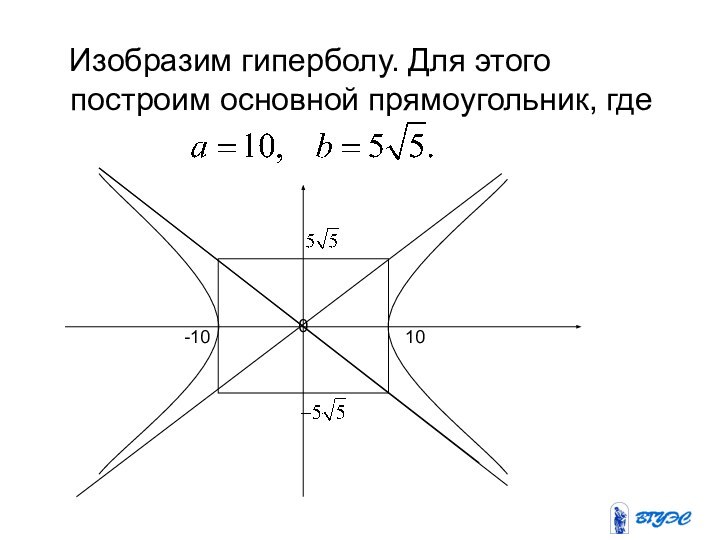
38. Изобразим гиперболу. Для этого построим основной прямоугольник, где 0-1010
39. Скачать презентацию
40. Похожие презентации

Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих координат х и у.

Окружность Окружностью называетсяся множество точек плоскости, равноудаленных от одной и той

Эллипс Эллипсом называется геометрическое место точек (плоскости), сумма расстояний которых от

Оси симметрии эллипса называются его осями, точка их пересечения- центром

Точки пересечения эллипса с осями координат называются вершинами эллипса. Это

Гипербола Гиперболой называется геометрическое место точек, разность расстояний которых от двух

Из уравнения гиперболы видно, что точек пересечения с осью Оу

Основной прямоугольник гиперболы Прямоугольник, проходящий через точки

Оси и полуоси гиперболы Принято говорить:

Асимптоты Гипербола имеет две асимптоты, т. е. прямые, к которым приближаются

Отношение называется эксцентриситетом гиперболы и является мерой ее «сплюснутости»,

Парабола Параболой называется геометрическое место точек, равноудаленных от данной точки

Если расположить ось Ох перпендикулярно директрисе и провести ее через

Общее уравнение кривой второго порядка Уравнение кривой второго порядка может

Пример Привести уравнение 2х²+3у²-16х-64=0 кривой второго порядка к каноническому виду

Для того чтобы привести уравнение кривой к каноническому виду, выделим

Это каноническое уравнение эллипса. Полуоси этого эллипса соответственно равны:

Пример Составить каноническое уравнение гиперболы, зная, что расстояние между ее фокусами

Тогда малая полуось Уравнение гиперболы имеет вид

Пример Составить уравнение гиперболы, если расстояние между вершинами ее равно 20,

Изобразим гиперболу. Для этого построим основной прямоугольник, где 0-1010

Пример Парабола симметрична относительно оси Ох, проходит через точку А(4;-1), а

Слайды презентации

Слайд 2 Кривой второго порядка называется линия, определяемая

уравнением второй степени относительно текущих координат х и у.

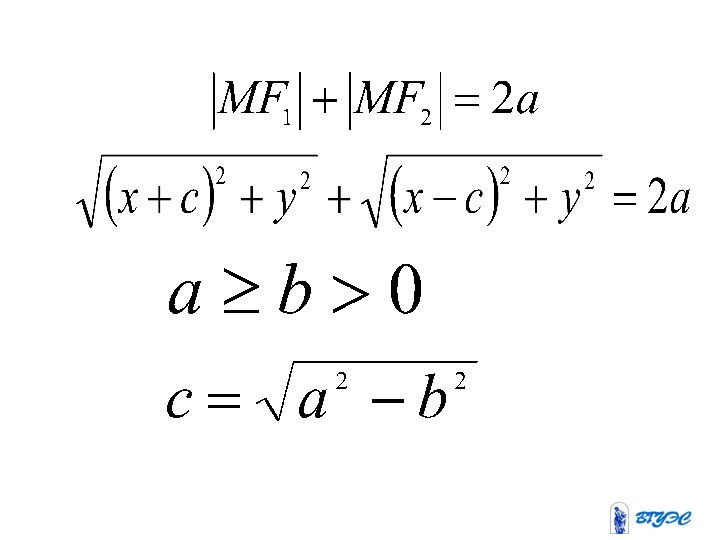
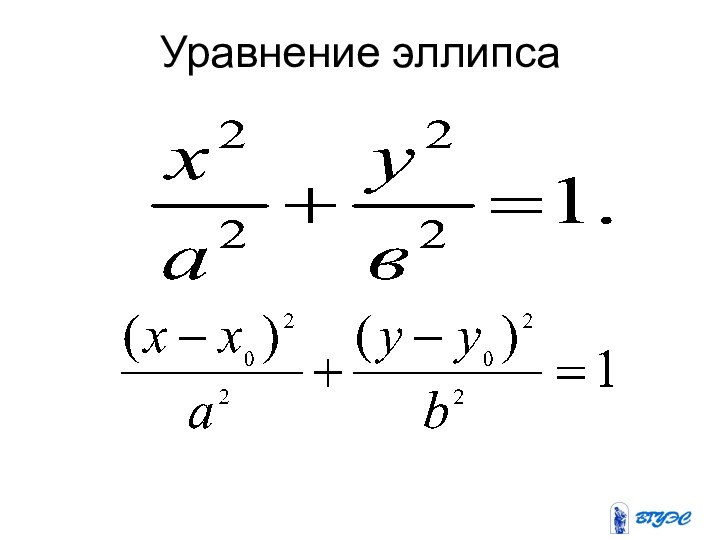
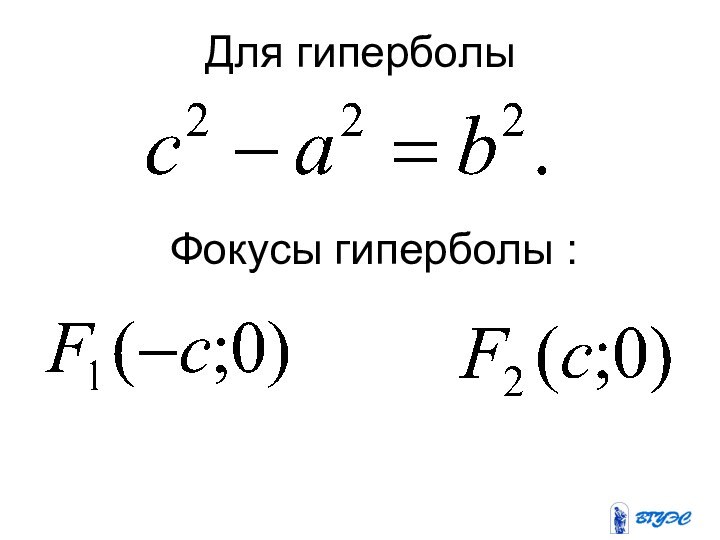
Слайд 3 Окружность
Окружностью называетсяся множество точек плоскости, равноудаленных

от одной и той же точки плоскости, называемой центром

окружности.
Уравнение окружности

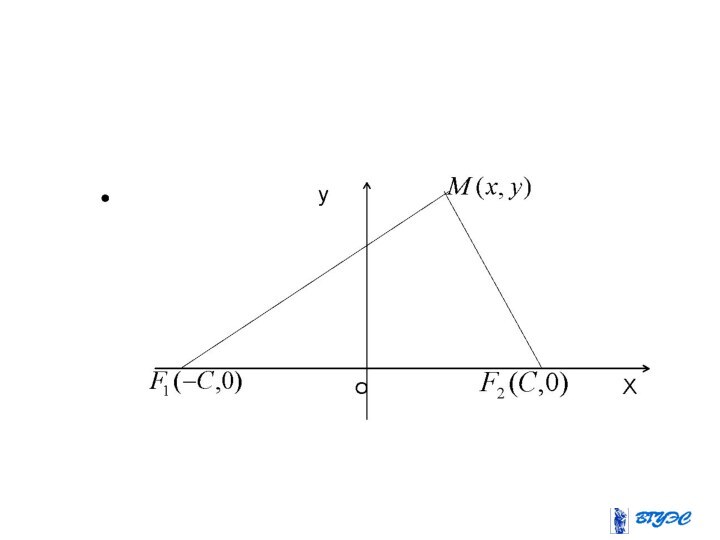
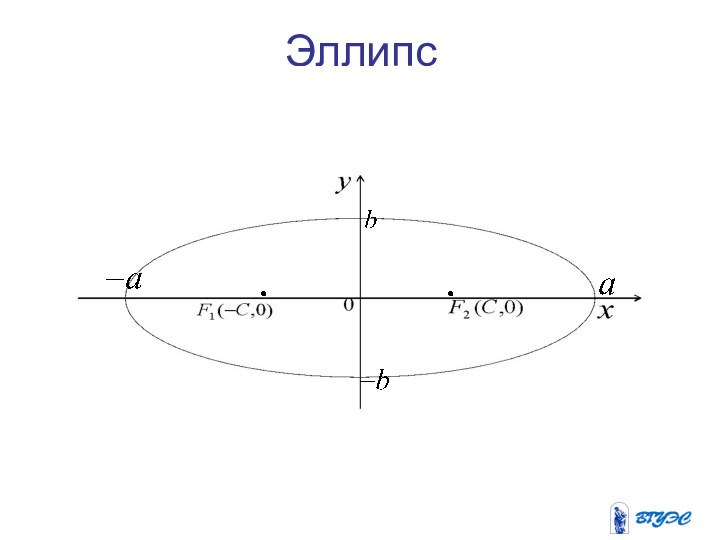
Слайд 4 Эллипс
Эллипсом называется геометрическое место точек (плоскости),

сумма расстояний которых от двух данных точек, называемых фокусами

этого эллипса, есть величина постоянная.

Слайд 7 Уравнение эллипса

Слайд 8 Эллипс

Слайд 9 Оси симметрии эллипса называются его осями,

точка их пересечения- центром эллипса, ось, на которой находятся

фокусы (в данном случае это ось абсцисс) называется фокальной осью.

Слайд 10 Точки пересечения эллипса с осями координат

называются вершинами эллипса. Это точки с координатами

Числа называются полуосями эллипса.

Слайд 11 Отношение

,

называется эксцентриситетом эллипса и характеризует его форму, ничего не говоря о его размерах. Чем меньше эксцентриситет, тем меньше подкоренное выражение в числителе дроби, тем меньше малая полуось отличается от большой и , значит, тем меньше эллипс вытянут вдоль фокальной оси.

Слайд 12 Замечание

Если

,то фокальной осью является

Фокусы :

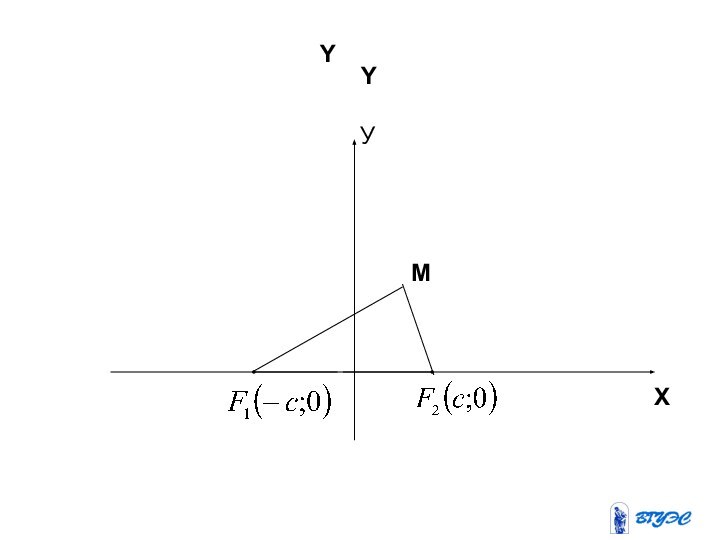
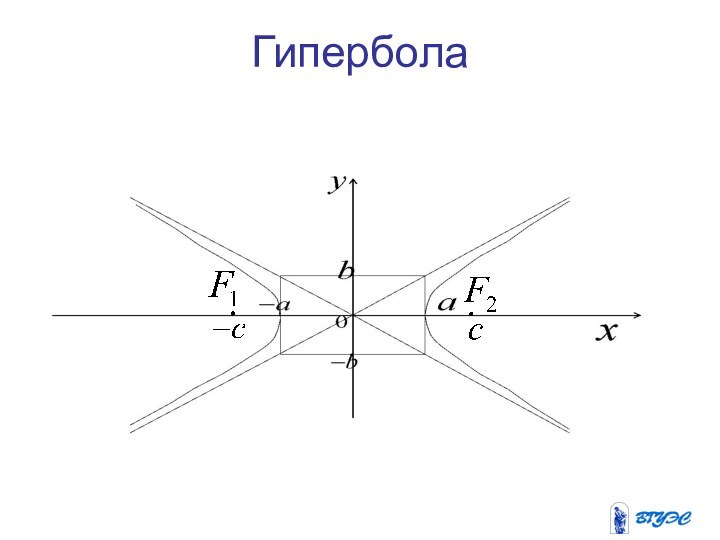
Слайд 13 Гипербола
Гиперболой называется геометрическое место точек, разность расстояний

которых от двух данных точек плоскости, называемых фокусами, есть

величина постоянная.

Слайд 14 X
Y
Y
M
У

Слайд 15 Уравнение гиперболы

Слайд 16 Гипербола

Слайд 17 Из уравнения гиперболы видно, что точек

пересечения с осью Оу нет. Ось Ох называют действительной

осью, а ось Оу – мнимой осью гиперболы. Гипербола имеет две вершины, лежащие на фокальной оси. Это точки

и

Слайд 18 Основной прямоугольник гиперболы

Прямоугольник, проходящий через

Основной прямоугольник гиперболы Прямоугольник, проходящий через точки со сторонами,

точки

со сторонами, параллельными осям

координат, называется основным прямоугольником гиперболы.

Слайд 19 Для гиперболы

Фокусы гиперболы :

Слайд 20 Оси и полуоси гиперболы

Принято говорить:

Оси и полуоси гиперболы Принято говорить: и

и -

действительная и мнимая оси

и - действительная и мнимая
полуоси
- фокальная ось

Слайд 21 Асимптоты
Гипербола имеет две асимптоты, т.

Асимптоты Гипербола имеет две асимптоты, т. е. прямые, к которым

е. прямые, к которым приближаются точки этой кривой при

неограниченном их удалении от начала координат вдоль по гиперболе в бесконечность. Их уравнения

Слайд 22 Отношение

называется эксцентриситетом гиперболы

и является мерой ее «сплюснутости», т. е. чем меньше

эксцентриситет, тем меньше отношение полуосей гиперболы, а, значит, тем сильнее вытянут ее основной прямоугольник

Слайд 23 Замечание

Для гиперболы

-мнимая ось ,а -действительная

ось

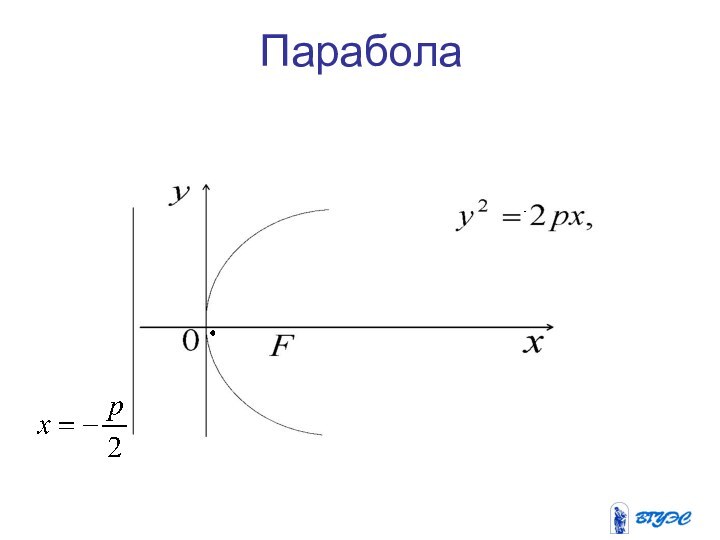
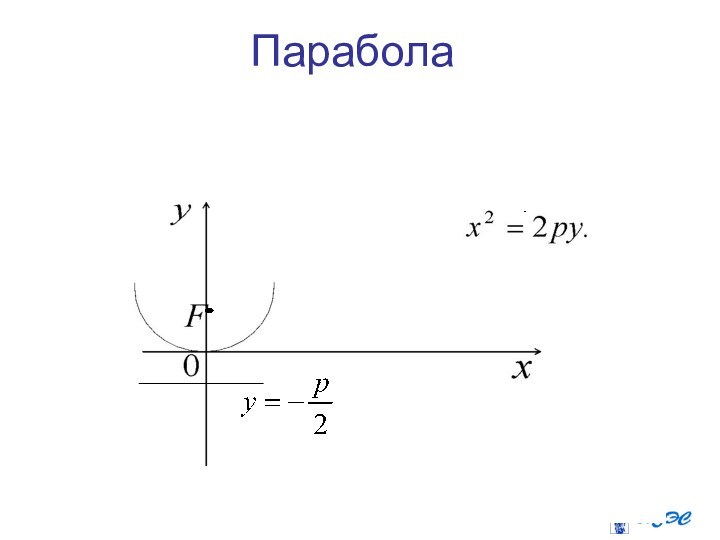
Слайд 24 Парабола
Параболой называется геометрическое место точек, равноудаленных

от данной точки плоскости, называемой фокусом, и данной прямой,

называемой директрисой.

Слайд 25 Если расположить ось Ох перпендикулярно директрисе

и провести ее через фокус в направлении от директрисы

к фокусу, обозначив при этом расстояние от фокуса до директрисы р, то можно показать, что в этом случае уравнение параболы будет иметь вид:
а если через фокус провести ось Оу, то уравнение имеет вид:

Слайд 26 Парабола

Слайд 27 Фокус параболы -

, вершина параболы

– в точке директриса параболы это прямая

Слайд 28 Парабола

Слайд 29 Фокус этой параболы

вершина

такой параболы находится в точке , директриса параболы- это прямая

Слайд 30 Самостоятельно изучить параболы

Слайд 31 Общее уравнение кривой второго порядка
Уравнение

кривой второго порядка может иметь вид

В простейшем случае при В=0 можно определить тип кривой, определяемой общим уравнением, выделяя полные квадраты переменных и сводя общее уравнение к каноническому уравнению той или иной кривой.

Слайд 32 Пример
Привести уравнение 2х²+3у²-16х-64=0 кривой второго

порядка
к каноническому виду и найти ее центр,

полуоси, эксцентриситет, и, если кривая имеет асимптоты, уравнения асимптот.

Слайд 33 Для того чтобы привести уравнение кривой

к каноническому виду, выделим полный квадрат переменной х. Для

этого произведем преобразования:
2(х²-8х)+3у²-64=0;
2(х²-8х+16-16)+3у²-64=0.
2((х-4)²-16)+3у²-64=0;
2(х-4)²+3у²-32-64=0; 2(х-4)²+3у²=96. Разделим теперь обе части уравнения на 96 и получим уравнение