Презентация на тему Квадратичная функция 9 класс

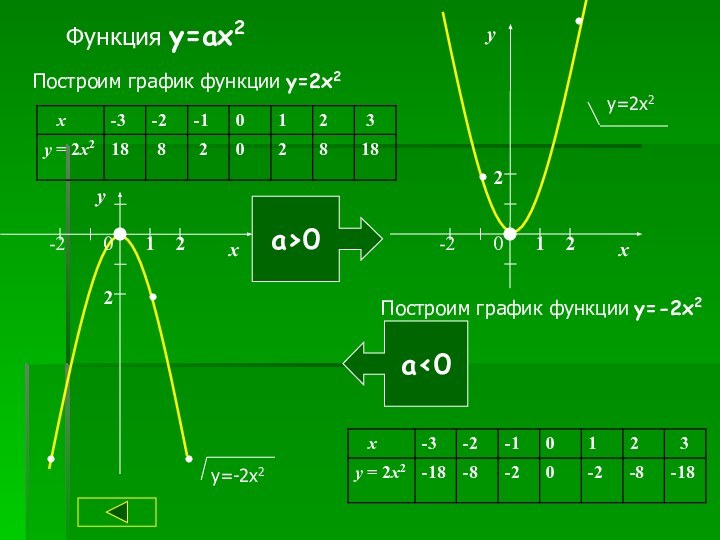
ах2
Сдвиг графика у = ах2
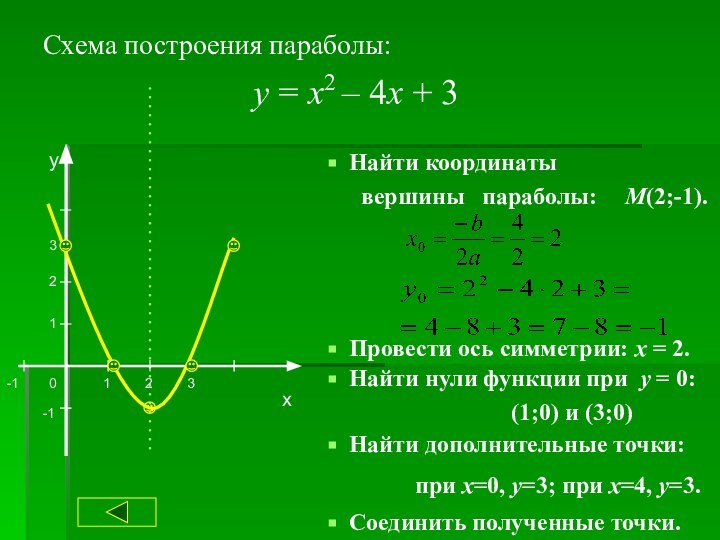
Способы построения параболы
Квадратичная функция в

заданиях ГИА
Примеры и комментарии
Задания ГИА

Резюме

функция
Квадратичной

функцией называют функцию, которую можно задать формулой вида
y = ax2 + bx + c, где a, b и с - некоторые числа, причём а ≠ 0.

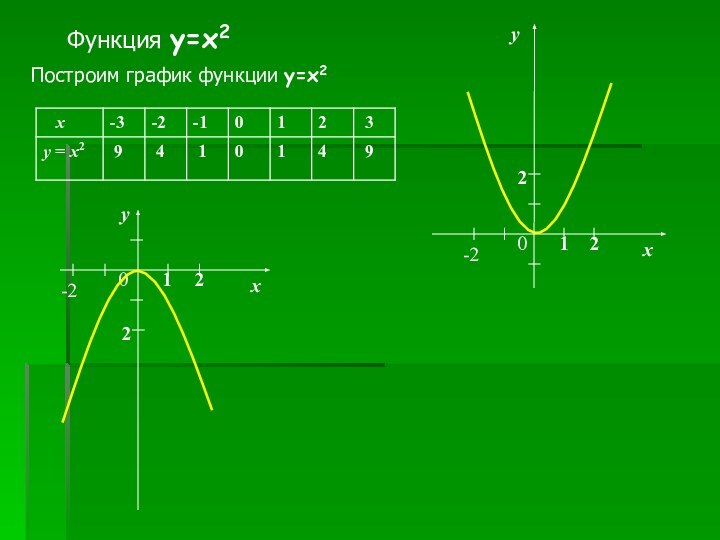
График любой квадратичной
функции – парабола.

= b2 – 4ac - дискриминант
M(x0,y0) – вершина параболы:

Уравнение параболы, проходящей через точку M:
y = a(x – x0)2 + y0
x1, x2 – корни параболы:
ax2 + bx + c = 0

осью Ох)
2.Точки пересечения с осью Оy
3.Возрастание функции( если X2>X1,

то f (X2)>f (X1)):
с возрастанием аргумента увеличивается значение функции.
Убывание функции( если X2>X1, то f (X2)с возрастанием аргумента уменьшается значение функции
- аргумент и функция связаны противоположными знаками.
4. Промежутки знакопостоянства : f (x) >0 и f (x)<0.
5. Непрерывность функции (разрыв - нельзя
провести график не отрываясь).
6. Наибольшее и наименьшее значение.

функции y=-2x2
у=-2х2
у
0
-2
2
1
2
0
х
-2
2
1
2
у
у=2х2

a≠0,
является парабола с вершиной в
начале координат;
её осью симметрии

служит ось y;
при a>0 ветви параболы направлены вверх,
при a<0 ветви вниз.

функции
При a>0 ветви параболы направлены вверх
При a

параболы направлены вниз

у = ах²

= x2
y = 2x2
y = 0,5x2
1. Д(у) = R
2.

Е(у)= [0; +∞)
3. четная, т.к. у(-х) = у(х)
4. Возрастает
на промежутке [0; +∞)
5. Убывает
на промежутке (-∞; 0]
6. Наименьшее значение
равное 0 при х = 0

y = - x2
y = - 2x2
y =

- 0,5x2

y

1. Д(у) = R
2. Е(у)= (-∞; 0]
3. четная, т.к. у(-х) = у(х)
4. Возрастает
на промежутке (-∞; 0]
5. Убывает
на промежутке [0; +∞)
6. Наибольшее значение
равное 0 при х = 0

координат
1. Чтобы построить график функции y = ax2 +

g , нужно перенести параболу y = ax2 вдоль оси на g единиц вверх, если g > 0, или на | g | единиц вниз, если g < 0. При этом вершина параболы окажется в точке (0; g).
2. Чтобы построить график функции y = a(x + p)2, нужно перенести параболу y = ax2 вдоль оси x на p единиц влево, если p > 0, или на | p | единиц вправо, если p < 0.При этом вершина параболы окажется в точке (- p ; 0).
3. Чтобы построить график функции y = a(x + p )2 + g, нужно перенести параболу y = ax2 вдоль оси x на p единиц влево, если p >0, или на | p | единиц вправо, если p < 0 и вдоль оси y на g единиц вверх, если g > 0, или на | g | единиц вниз, если g < 0. При этом вершина параболы окажется в точке (- p ; g ).

0

2) g < 0

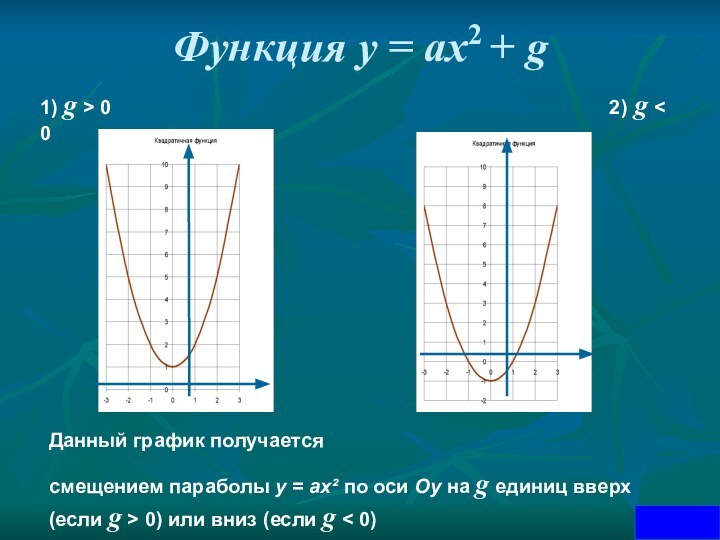
Данный график получается
смещением параболы у = ах² по оси Оу на g единиц вверх (если g > 0) или вниз (если g < 0)

0

2) р < 0

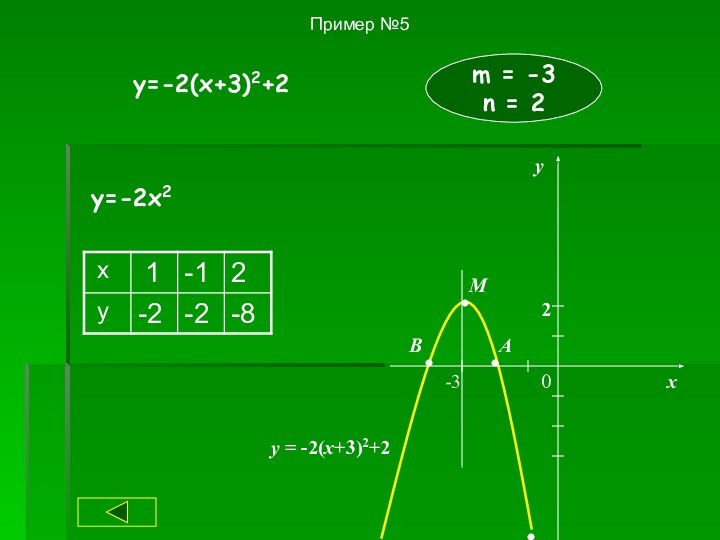
График получается
смещением параболы у = ах² по оси Ох на р единиц вправо (если р > 0) или влево (если р < 0)

№1
Пример №2
Пример №4
Пример №3
Схема
Пример №5

вершину параболы.
Провести через вершину параболы прямую,

параллельную оси ординат, - ось симметрии
параболы.
Найти нули функции, если они есть, и построить
на оси абсцисс соответствующие точки параболы.
Построить дополнительные точки.
Провести через построенные точки параболу.

свободному члену квадратного трёхчлена ax2-bx+c.

графика функции y=ax2
на m единичных отрезков по оси

Ох и
на n единичных отрезков по оси Оу.

3
Найти координаты
вершины параболы: М(2;-1).

Провести ось симметрии: х = 2.

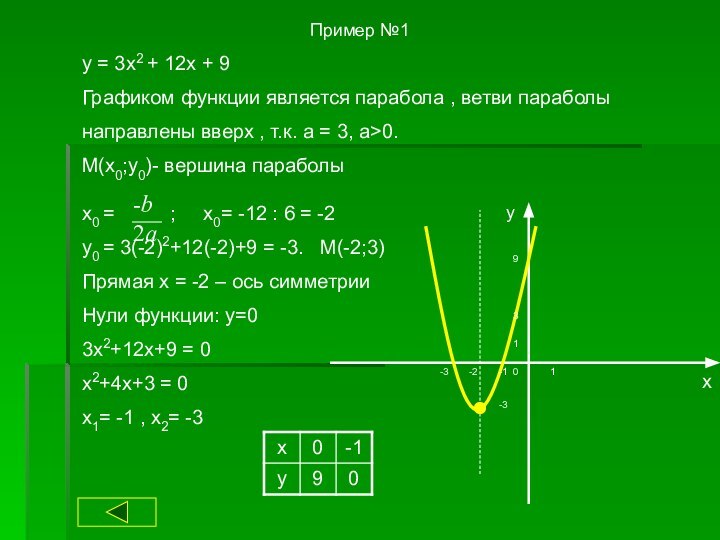
Найти нули функции при у = 0:
(1;0) и (3;0)

Найти дополнительные точки:
при х=0, у=3; при х=4, у=3.

Соединить полученные точки.

Графиком функции является парабола , ветви параболы
направлены вверх

, т.к. а = 3, a>0.
M(x0;y0)- вершина параболы

x0 = ; x0= -12 : 6 = -2
y0 = 3(-2)2+12(-2)+9 = -3. M(-2;3)
Прямая х = -2 – ось симметрии
Нули функции: y=0
3x2+12x+9 = 0
x2+4x+3 = 0
x1= -1 , x2= -3

0

1

1

-1

-3

-2

-3

9

3

у

x

2а

-b

5
Графиком функции является парабола , ветви параболы
направлены

вверх , т.к. а = ¼ , a>0.
M(x0;y0)- вершина параболы

x0 = ; x0= -2 : ½ = -4
y0 = ¼ (-4)2+2(-4)-5 = -9. M(-4;-9)
Прямая х = -4 – ось симметрии
Нули функции: y=0
¼ x2 + 2x – 5 = 0
x2 + 8x – 20 = 0
x1= -10 , x2= 2

-10

0

1

2

-1

-3

-4

-6

-9

у

-b
2а

x

точки графика, имеющие ординату, равную 5. Для этого решаем

уравнение x2 – 4x + 5 = 5. Получаем: х1 = 0, х2 = 4
2) Точки А (0; 5) и В (4; 5) лежат на параболе и имеют одинаковую ординату. Эти точки симметричны относительно оси симметрии параболы, поэтому ось симметрии проходит через середину отрезка АВ. Т.к. абсцисса точки А равна 0, а т. В равна четырём , то уравнение оси параболы х = 2.
3) Подставим значение х в уравнение. Получаем координаты вершины параболы: х0 = 2, у0 = 1.
4) Отмечаем на координатной плоскости т. С (2; 1), построим параболу, проходящую через три точки А, В, С.

у=х2-4х+5

А

В

С

0

х

5

у

параболу y=2x2;
2)Перенесем ее на 1 единицу влево и на

3 единицы вниз –
в результате получится график заданной функции y=2(x+1)2 - 3 (см.рис)
Действия , которые мы выполнили для построения графика , можно описать такой схемой:

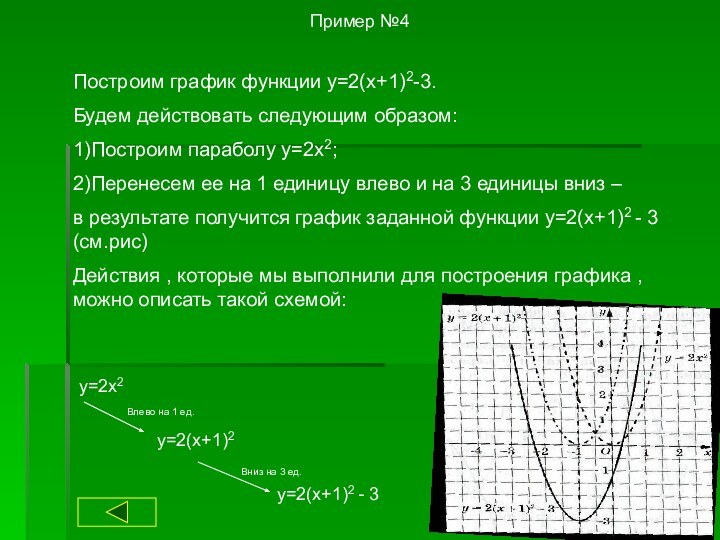
y=2x2

y=2(x+1)2

y=2(x+1)2 - 3

Влево на 1 ед.

Вниз на 3 ед.