Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Матан

Содержание

ПОНЯТИЕ МНОЖЕСТВА МНОЖЕСТВО – совокупность объектовлюбой природы, объединенныхпо какому-либо признаку.Объекты, составляющие множество, называются элементами этого множества.Обозначается: А – множество, а – элемент множества А
МАТЕМАТИЧЕСКИЙ АНАЛИЗ ПОНЯТИЕ МНОЖЕСТВА МНОЖЕСТВО – совокупность объектовлюбой природы, объединенныхпо какому-либо признаку.Объекты, составляющие множество, ПРИМЕРЫ МНОЖЕСТВ: Множество студентов ВУЗаМножество рыб в аквариумеМножество судов на причале Пусть Х и У – два множества.Между ними возможны следующие отношения:Множество, не 2Если все элементы множества Х содержатся в У, то Х является подмножеством У. 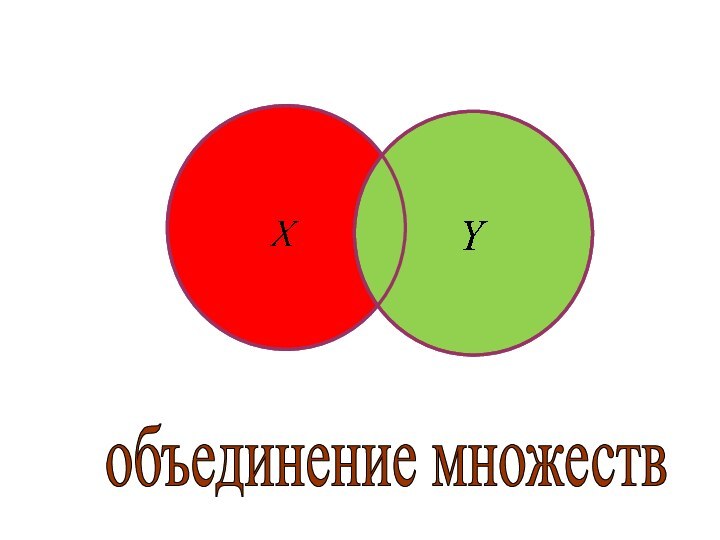3ОБЪЕДИНЕНИЕМ двух множеств Х и Уназывается множество Z, состоящееиз всех элементов, принадлежащиххотя объединение множеств 4ПЕРЕСЕЧЕНИЕМ двух множеств Х и Уназывается множество Z, состоящееиз всех элементов, одновременно пересечение множеств 5РАЗНОСТЬЮ двух множеств Х и Уназывается множество Е, состоящееиз всех элементов множества разность множеств ПРИМЕР.Даны множества Х={2;4;6;8} Y={2;4;5;9}Найти пересечение, объединение и разность этих множеств. РЕШЕНИЕ: ФУНКЦИИ И ИХ СВОЙСТВА Если каждому элементу х множества Х ставитсяв соответствие Свойства функций Функция y=f(x) называется четной, еслидля любого х 1. Четность Функция y=f(x) называется нечетной, еслидля любого х Если оба эти условия не Функция y=f(x) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента - функция возрастает - функция убывает Функция y=f(x) называется периодичной спериодом Т, не равным нулю, если для любого х выполняется равенство:3. Периодичность Например:-периодичная с периодом, равным 2П, т.к. для любого х Функция x=φ(y) определенная на множестве У с областью значений Х,называется обратной к ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ Если каждому натуральному числу n по некоторому закону поставлено Числа a1,a2…an называются членами последовательности, а число an называется общим членом или n-ым членом данной последовательности.Например:12 Изобразим члены последовательности точками на числовой оси.Можно заметить, что члены последовательности с Последовательность {an} называется ограниченной сверху (снизу), если существует такое число М (m), Последовательность {an} называется ограниченной, если она ограничена сверху и снизу: 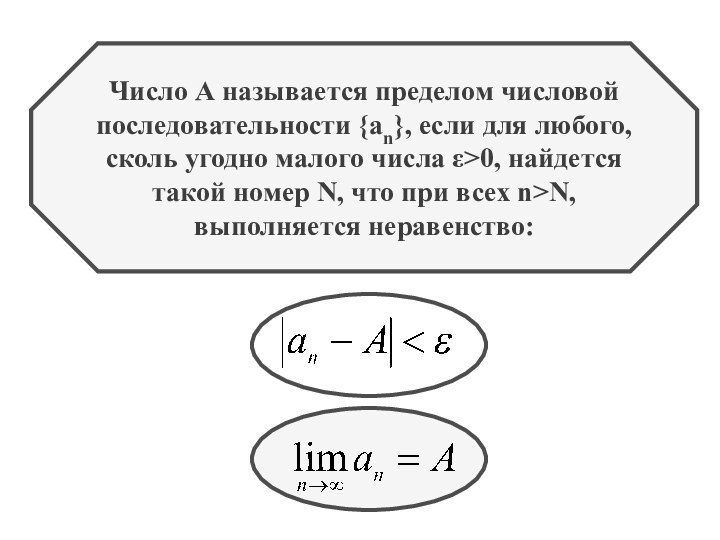Число А называется пределом числовой последовательности {an}, если для любого,сколь угодно малого ПРИМЕР.Дана последовательностьПоказать, что предел этой последовательностиравен 1.3 РЕШЕНИЕ:Пусть ε=0.1Тогда неравенствопримет вид: Если ε=0.01, то неравенство выполняется при Для любого ε >0, неравенство выполняется Рассмотрим геометрический смысл предела числовой последовательности. Для этого изобразим члены последовательности (3) точками на числовой оси. Неравенство равносильно двойному неравенству которое соответствует попаданию членов последовательности в ε – окрестность точки А. Число А называется пределом функции у=f(x), при х стремящемся к бесконечности, если Рассмотрим геометрический смысл этого определения.Неравенстворавносильно двойному неравенствучто соответствует расположению части графика у=f(x) в полосе шириной 2ε. Число А называется пределом функции у=f(x), при х→x0, (или в точке x0)если
Слайды презентации

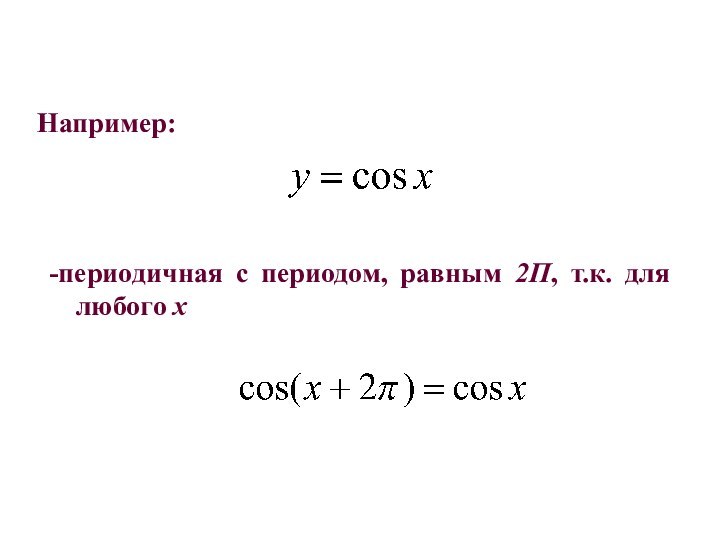
Слайд 2 ПОНЯТИЕ МНОЖЕСТВА
МНОЖЕСТВО – совокупность объектов
любой природы, объединенных
по

ПОНЯТИЕ МНОЖЕСТВА МНОЖЕСТВО – совокупность объектовлюбой природы, объединенныхпо какому-либо признаку.Объекты, составляющие

какому-либо признаку.
Объекты, составляющие множество, называются элементами этого множества.
Обозначается:
А

– множество, а – элемент множества А

Слайд 3 ПРИМЕРЫ МНОЖЕСТВ: Множество студентов ВУЗа
Множество рыб в аквариуме
Множество

ПРИМЕРЫ МНОЖЕСТВ: Множество студентов ВУЗаМножество рыб в аквариумеМножество судов на причале

судов на причале

Слайд 4 Пусть Х и У – два множества.
Между ними

Пусть Х и У – два множества.Между ними возможны следующие отношения:Множество,

возможны следующие отношения:
Множество, не содержащее ни одного
элемента, называется

пустым 0.

1

Если оба множества состоят из одних
и тех же элементов, то они совпадают.

Х=У

Слайд 5 2
Если все элементы множества Х
содержатся в У,

2Если все элементы множества Х содержатся в У, то Х является подмножеством У.

то Х является
подмножеством У.

Слайд 6 3
ОБЪЕДИНЕНИЕМ двух множеств Х и У
называется множество Z,

3ОБЪЕДИНЕНИЕМ двух множеств Х и Уназывается множество Z, состоящееиз всех элементов,

состоящее
из всех элементов, принадлежащих
хотя бы одному из данных множеств.

Слайд 7 объединение множеств

объединение множеств

Слайд 8 4
ПЕРЕСЕЧЕНИЕМ двух множеств Х и У
называется множество Z,

4ПЕРЕСЕЧЕНИЕМ двух множеств Х и Уназывается множество Z, состоящееиз всех элементов,

состоящее
из всех элементов, одновременно
принадлежащих каждому из данных
множеств.

Слайд 9 пересечение множеств

пересечение множеств

Слайд 10 5
РАЗНОСТЬЮ двух множеств Х и У
называется множество Е,

5РАЗНОСТЬЮ двух множеств Х и Уназывается множество Е, состоящееиз всех элементов

состоящее
из всех элементов множества Х,
которые не принадлежат множеству

У.


Слайд 11 разность множеств

разность множеств

Слайд 12 ПРИМЕР.
Даны множества
Х={2;4;6;8} Y={2;4;5;9}
Найти пересечение, объединение и
разность

ПРИМЕР.Даны множества Х={2;4;6;8} Y={2;4;5;9}Найти пересечение, объединение и разность этих множеств.

этих множеств.

Слайд 13 РЕШЕНИЕ:

РЕШЕНИЕ:

Слайд 14 ФУНКЦИИ И ИХ СВОЙСТВА
Если каждому элементу х

ФУНКЦИИ И ИХ СВОЙСТВА Если каждому элементу х множества Х ставитсяв

множества Х ставится
в соответствие определенный элемент у
множества У,

то говорят, что на множестве Х
задана функция


Слайд 15 Свойства функций
Функция y=f(x) называется четной, если
для любого

Свойства функций Функция y=f(x) называется четной, еслидля любого х 1. Четность

х
1. Четность

Слайд 16 Функция y=f(x) называется нечетной, если
для любого х

Если

Функция y=f(x) называется нечетной, еслидля любого х Если оба эти условия

оба эти условия не выполняются, то функция называется функцией

общего вида.

График четной функции симметричен
относительно оси ординат.
График нечетной функции симметричен
относительно начала координат.

Слайд 17 Функция y=f(x) называется возрастающей
(убывающей) на промежутке Х,

Функция y=f(x) называется возрастающей (убывающей) на промежутке Х, если большему значению

если
большему значению аргумента из этого
промежутка соответствует большее
(меньшее) значение

функции.

2. Монотонность

Слайд 18
- функция возрастает


- функция возрастает

Слайд 19 - функция убывает



- функция убывает

Слайд 20 Функция y=f(x) называется периодичной с
периодом Т, не равным

Функция y=f(x) называется периодичной спериодом Т, не равным нулю, если для любого х выполняется равенство:3. Периодичность

нулю, если для
любого х выполняется равенство:
3. Периодичность

Слайд 21 Например:
-периодичная с периодом, равным 2П, т.к. для любого

Например:-периодичная с периодом, равным 2П, т.к. для любого х

Слайд 22 Функция x=φ(y) определенная на
множестве У с областью

Функция x=φ(y) определенная на множестве У с областью значений Х,называется обратной

значений Х,
называется обратной к функции y=f(x) .
Графики взаимно обратных

функций
симметричны относительно биссектрисы
первого и третьего координатных углов.

Слайд 23

Слайд 24 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Если каждому натуральному числу n

ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ Если каждому натуральному числу n по некоторому закону

по
некоторому закону поставлено
в соответствие
определенное число an

, то говорят, что
задана числовая последовательность


Слайд 25 Числа a1,a2…an называются членами последовательности, а число an

Числа a1,a2…an называются членами последовательности, а число an называется общим членом или n-ым членом данной последовательности.Например:12

называется общим членом или n-ым членом данной последовательности.
Например:
1
2

Слайд 26 Изобразим члены последовательности точками на числовой оси.






Можно заметить,

Изобразим члены последовательности точками на числовой оси.Можно заметить, что члены последовательности

что члены последовательности с ростом n сколь угодно близко

приближаются к нулю.

Слайд 27 Последовательность {an} называется
ограниченной сверху (снизу), если существует

Последовательность {an} называется ограниченной сверху (снизу), если существует такое число М


такое число М (m), что любой элемент этой
последовательности удовлетворяет


неравенству:


Слайд 28 Последовательность {an} называется
ограниченной, если она ограничена
сверху

Последовательность {an} называется ограниченной, если она ограничена сверху и снизу:

и снизу:

Слайд 29 Число А называется пределом числовой
последовательности {an}, если

Число А называется пределом числовой последовательности {an}, если для любого,сколь угодно

для любого,
сколь угодно малого числа ε>0, найдется
такой номер

N, что при всех n>N,
выполняется неравенство:



Слайд 30 ПРИМЕР.
Дана последовательность

Показать, что предел этой
последовательности
равен 1.
3

ПРИМЕР.Дана последовательностьПоказать, что предел этой последовательностиравен 1.3

Слайд 31 РЕШЕНИЕ:
Пусть ε=0.1
Тогда неравенство
примет вид:


РЕШЕНИЕ:Пусть ε=0.1Тогда неравенствопримет вид:

Слайд 32 Если ε=0.01, то неравенство выполняется при
Для любого

Если ε=0.01, то неравенство выполняется при Для любого ε >0, неравенство

ε >0, неравенство выполняется при
Т.е. для любого ε

>0 существует номер

Что для всех n>N, выполняется неравенство:


Слайд 33 Рассмотрим геометрический смысл предела числовой последовательности. Для этого

Рассмотрим геометрический смысл предела числовой последовательности. Для этого изобразим члены последовательности (3) точками на числовой оси.

изобразим члены последовательности (3) точками на числовой оси.

Слайд 34

Неравенство








равносильно двойному неравенству
которое соответствует попаданию членов

Неравенство равносильно двойному неравенству которое соответствует попаданию членов последовательности в ε – окрестность точки А.

последовательности в ε – окрестность точки А.

Слайд 35 Число А называется пределом функции
у=f(x), при х

Число А называется пределом функции у=f(x), при х стремящемся к бесконечности,

стремящемся
к бесконечности,
если для любого, сколь угодно малого

числа
ε>0, найдется такое положительное число
S, что при всех |x|>S, выполняется
неравенство:

ПРЕДЕЛ ФУНКЦИИ

Слайд 36 Рассмотрим геометрический смысл этого определения.
Неравенство
равносильно двойному неравенству
что соответствует

Рассмотрим геометрический смысл этого определения.Неравенстворавносильно двойному неравенствучто соответствует расположению части графика у=f(x) в полосе шириной 2ε.

расположению части графика у=f(x) в полосе шириной 2ε.

Слайд 37

Слайд 38 Число А называется пределом функции
у=f(x), при х→x0,

Число А называется пределом функции у=f(x), при х→x0, (или в точке

(или в точке x0)
если для любого, сколь угодно малого

числа
ε>0, найдется такое положительное число
δ, что при всех |x-x0|> δ, выполняется
неравенство:
  • Имя файла: matan.pptx
  • Количество просмотров: 109
  • Количество скачиваний: 0
- Предыдущая Средняя линия трапеции
Следующая - Формирование адекватной оценки знаний

Похожие презентации

Пропорция Пропорция 109
Громко прозвенел звонок - начинается урок Громко прозвенел звонок - начинается урок 132
Действия с дробями, Нахождение дроби и процентов от числа Действия с дробями, Нахождение дроби и процентов от числа 106
Презентация урока на тему: Предмет и аксиомы стереометрии Презентация урока на тему: Предмет и аксиомы стереометрии 106
Презентация Число 6, цифра 6 презентация к уроку по математике (1 класс) по теме Презентация Число 6, цифра 6 презентация к уроку по математике (1 класс) по теме 115
Презентация по геометрии на тему Поворот Презентация по геометрии на тему Поворот 172
Олимпийские игры. Презентация. презентация к уроку по математике (3 класс) Олимпийские игры. Презентация. презентация к уроку по математике (3 класс) 128
Приемы вычислений для случаев вида 60-24 Приемы вычислений для случаев вида 60-24 116
Открытый урок по теме Задачи на совместную работу 5 класс, 2010 (Дорофеев Г.В., Шарыгин И.Ф.) Открытый урок по теме Задачи на совместную работу 5 класс, 2010 (Дорофеев Г.В., Шарыгин И.Ф.) 176
Отношения. Пропорции.Подготовка к контрольной работе Отношения. Пропорции.Подготовка к контрольной работе 101
Сложение чисел с помощью координатной прямой Сложение чисел с помощью координатной прямой 123
Бесконечно убывающая геометрическая последовательность и ее сумма Бесконечно убывающая геометрическая последовательность и ее сумма 103
Свойства параллельных прямых Свойства параллельных прямых 118
Урок математики во 2 классе Умножение числа 9 и деление на 9 план-конспект урока по математике (2 класс) Урок математики во 2 классе Умножение числа 9 и деление на 9 план-конспект урока по математике (2 класс) 131
prezentatsiya microsoft office powerpoint prezentatsiya microsoft office powerpoint 95
точка, кривая, прямая, отрезок точка, кривая, прямая, отрезок 53
Тренажёр Счёт в пределах 100 тренажёр по математике (2 класс) Тренажёр Счёт в пределах 100 тренажёр по математике (2 класс) 122
Внеклассное мероприятие по математике Стенка на Стенку Внеклассное мероприятие по математике Стенка на Стенку 108
Презентация по математике к проекту Решай-ка! Презентация по математике к проекту Решай-ка! 120
Тренажёр по математике Тренажёр по математике 135
Математика и поэзия Математика и поэзия 127
Кафедра математики Кафедра математики 111
Игра Найди лишний предмет презентация по математике Игра Найди лишний предмет презентация по математике 102
Что мы знаем о числах великанах? Что мы знаем о числах великанах? 118
Презентация Занимательные примеры - на вычитание презентация к уроку по математике (подготовительная группа) Презентация Занимательные примеры - на вычитание презентация к уроку по математике (подготовительная группа) 128
Треугольник Треугольник 189
Презентация по математике Сложение и вычитание смешанных чисел.6 класс. ФГОС. Урок 1 Презентация по математике Сложение и вычитание смешанных чисел.6 класс. ФГОС. Урок 1 113
Урок по теме Умножение десятичной дроби на натуральное число Урок по теме Умножение десятичной дроби на натуральное число 104
Задачи для подготовки к ГИА и ЕГЭ Пропорциональные отрезки в прямоугольном треугольнике Задачи для подготовки к ГИА и ЕГЭ Пропорциональные отрезки в прямоугольном треугольнике 187
Двугранный угол Двугранный угол 136