- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многогранники
Содержание
- 2. Кубок Кеплера Иоганн Кеплер (1571 – 1630)
- 3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИВыпуклый многогранник называется правильным, если его
- 4. ТЕТРАЭДРНаиболее простым правильным многогранником является треугольная пирамида,
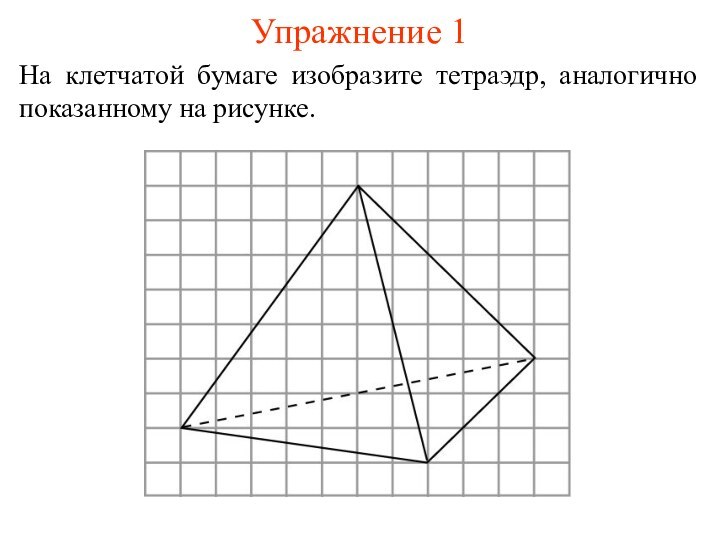
- 5. Упражнение 1На клетчатой бумаге изобразите тетраэдр, аналогично показанному на рисунке.
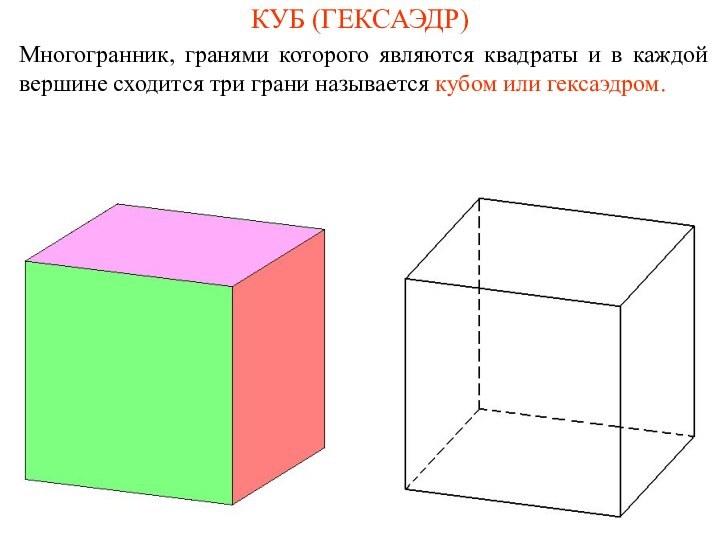
- 6. КУБ (ГЕКСАЭДР)Многогранник, гранями которого являются квадраты и
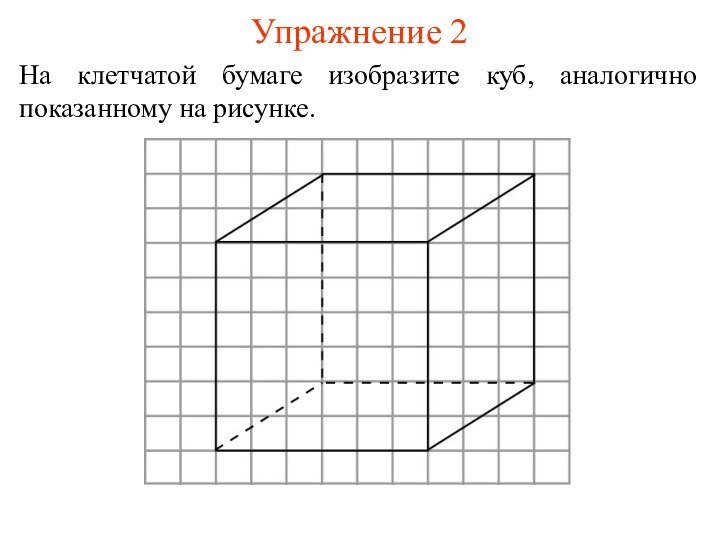
- 7. Упражнение 2На клетчатой бумаге изобразите куб, аналогично показанному на рисунке.
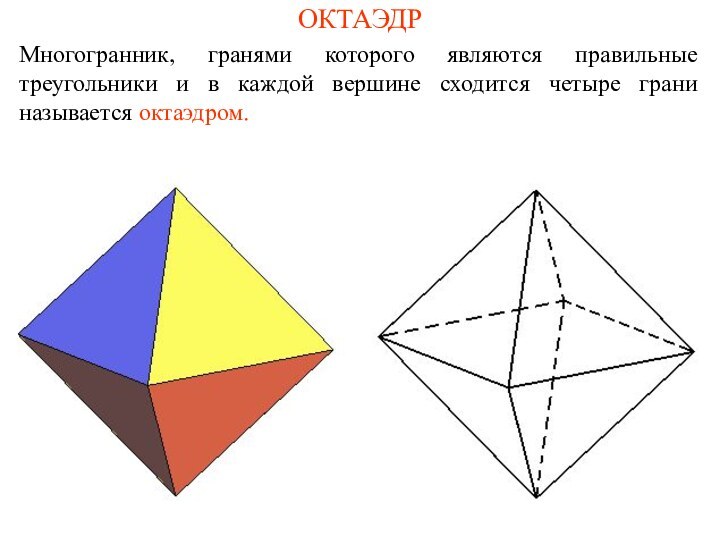
- 8. ОКТАЭДРМногогранник, гранями которого являются правильные треугольники и в каждой вершине сходится четыре грани называется октаэдром.
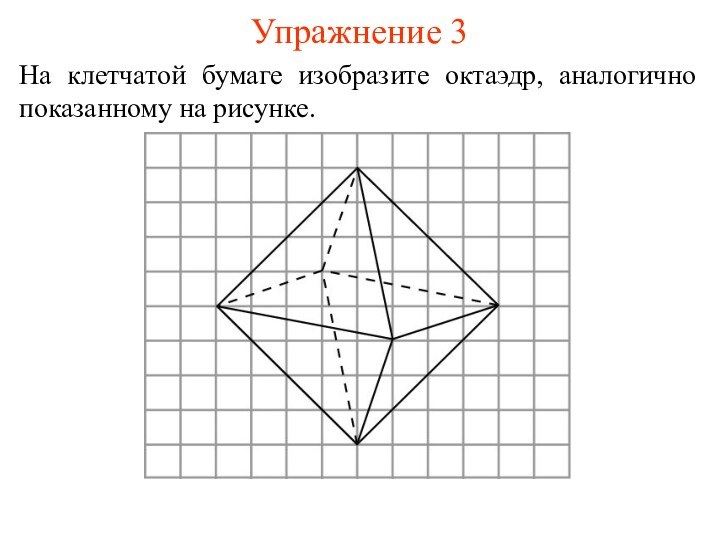
- 9. Упражнение 3На клетчатой бумаге изобразите октаэдр, аналогично показанному на рисунке.
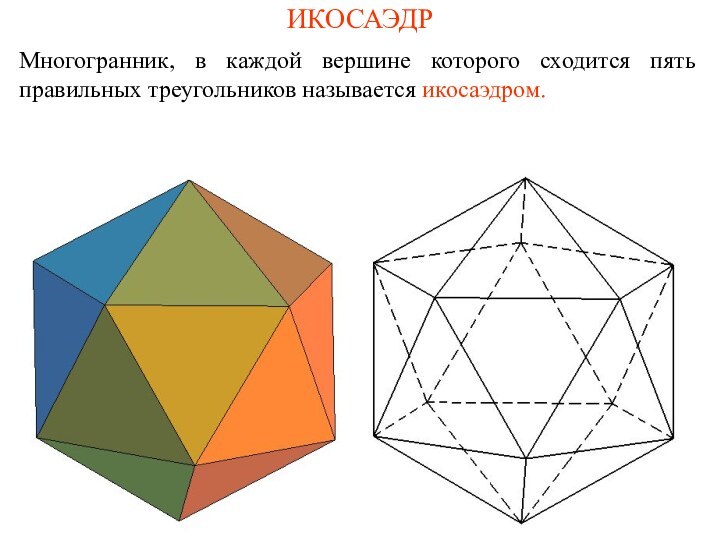
- 10. ИКОСАЭДРМногогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.
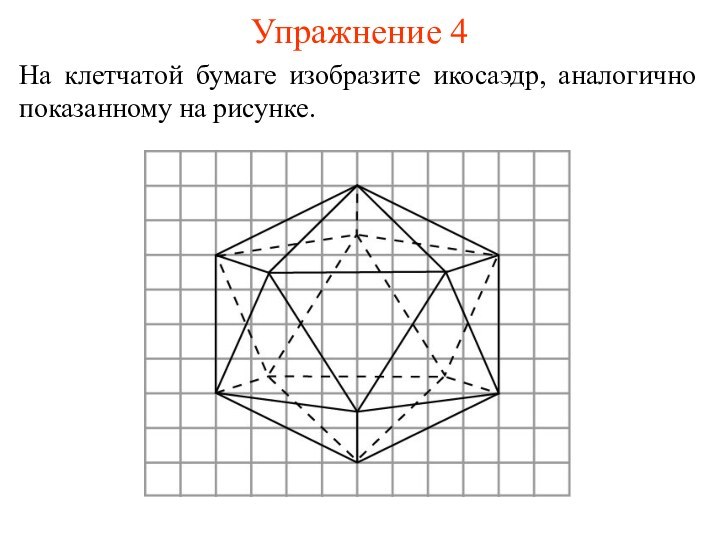
- 11. Упражнение 4На клетчатой бумаге изобразите икосаэдр, аналогично показанному на рисунке.
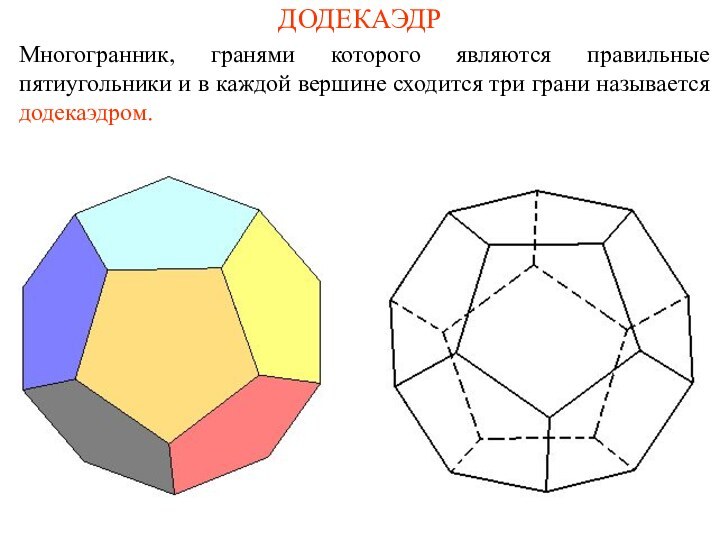
- 12. ДОДЕКАЭДРМногогранник, гранями которого являются правильные пятиугольники и в каждой вершине сходится три грани называется додекаэдром.
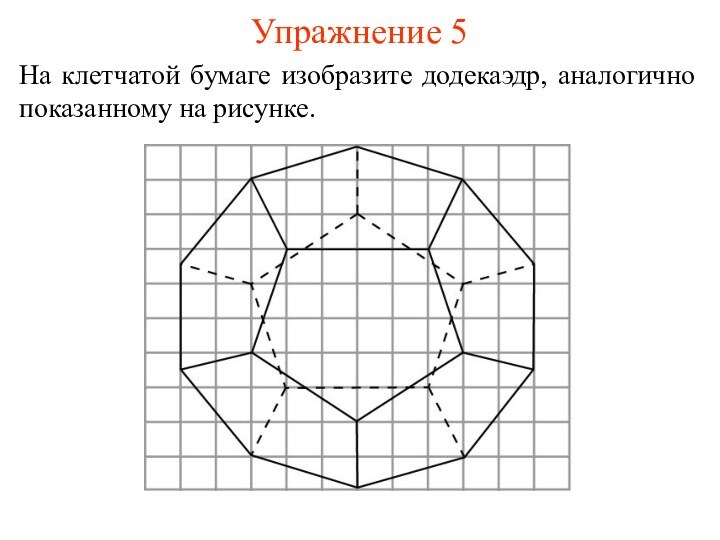
- 13. Упражнение 5На клетчатой бумаге изобразите додекаэдр, аналогично показанному на рисунке.
- 14. Упражнение 6Почему гранями правильного многогранника не могут
- 15. Упражнение 7Представьте многогранник - бипирамиду, сложенную из
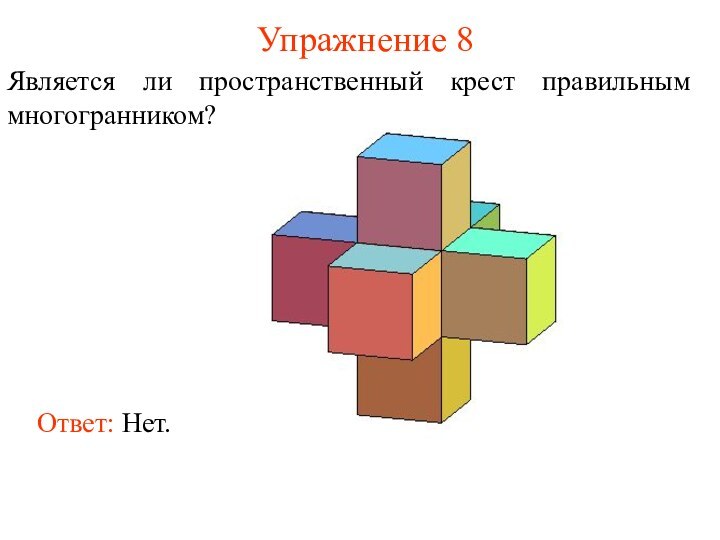
- 16. Упражнение 8Является ли пространственный крест правильным многогранником? Ответ: Нет.
- 17. Упражнение 9Сколько тетраэдров изображено на рисунке?Ответ: Пять.
- 18. Упражнение 10Сколько кубов изображено на рисунке?Ответ: Три.
- 19. Упражнение 11Сколько октаэдров изображено на рисунке?Ответ: Три.
- 20. Упражнение 12Соединение каких двух многогранников изображено на рисунке?Ответ: Икосаэдра и додекаэдра.
- 21. Упражнение 13Сколько вершин (В), ребер (Р) и
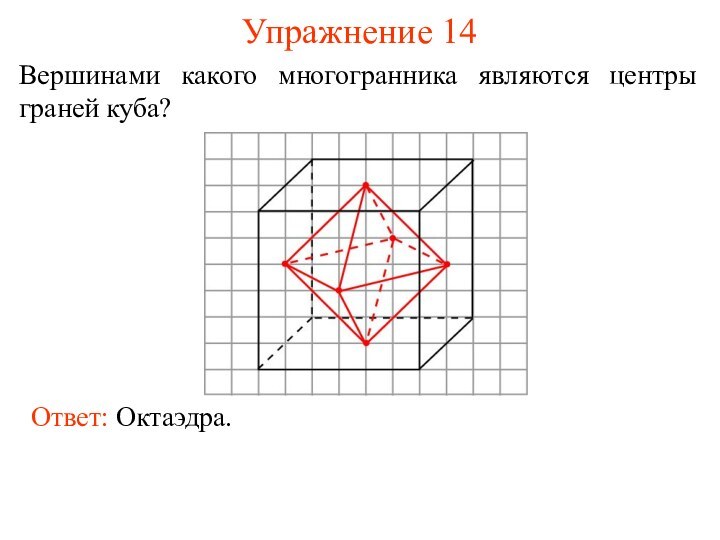
- 22. Упражнение 14Вершинами какого многогранника являются центры граней куба?
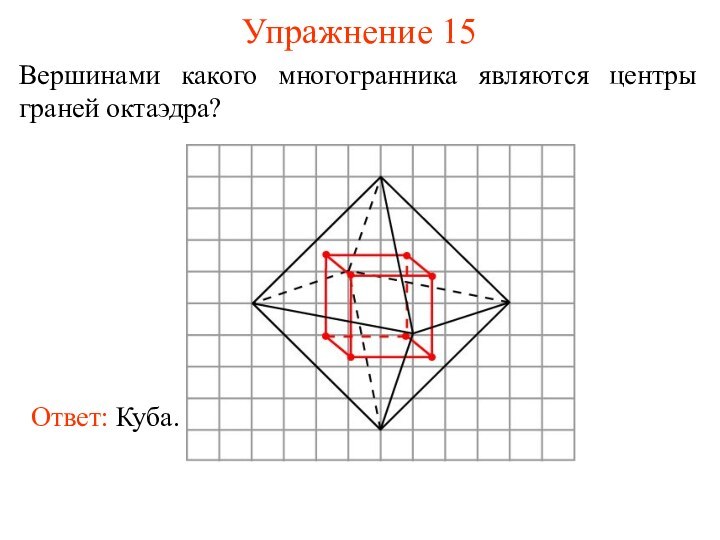
- 23. Упражнение 15Вершинами какого многогранника являются центры граней октаэдра?
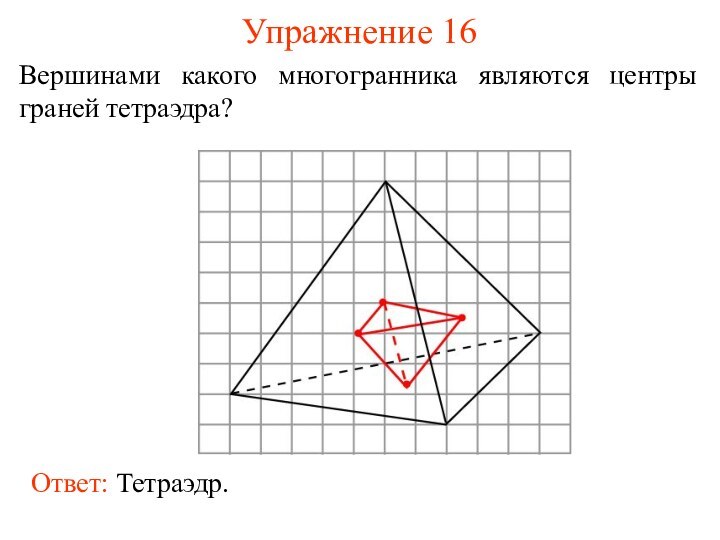
- 24. Упражнение 16Вершинами какого многогранника являются центры граней тетраэдра?
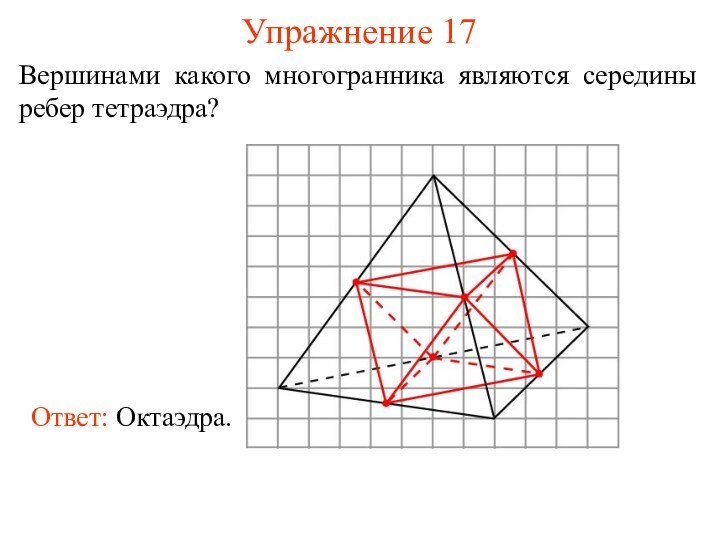
- 25. Упражнение 17Вершинами какого многогранника являются середины ребер тетраэдра?
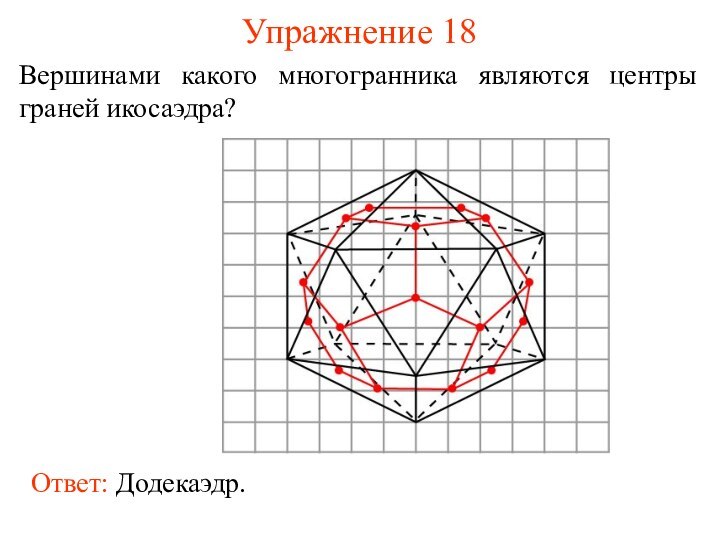
- 26. Упражнение 18Вершинами какого многогранника являются центры граней икосаэдра?
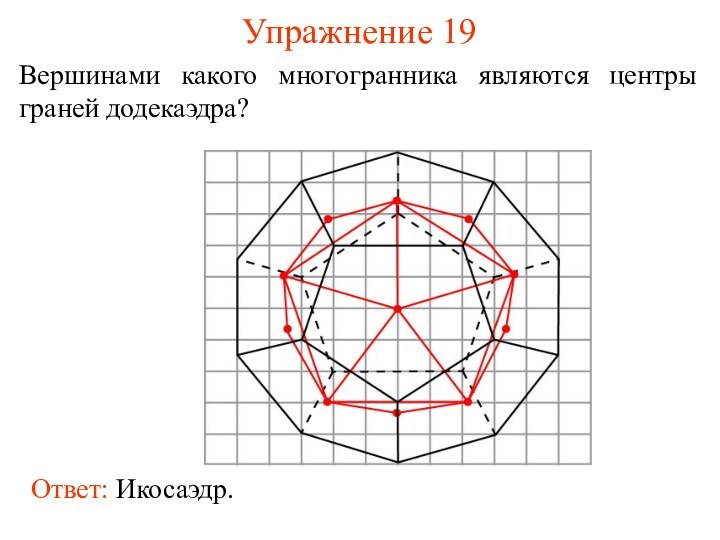
- 27. Упражнение 19Вершинами какого многогранника являются центры граней додекаэдра?
- 28. Двойственные многогранникиДва правильных многогранника называются двойственными, если
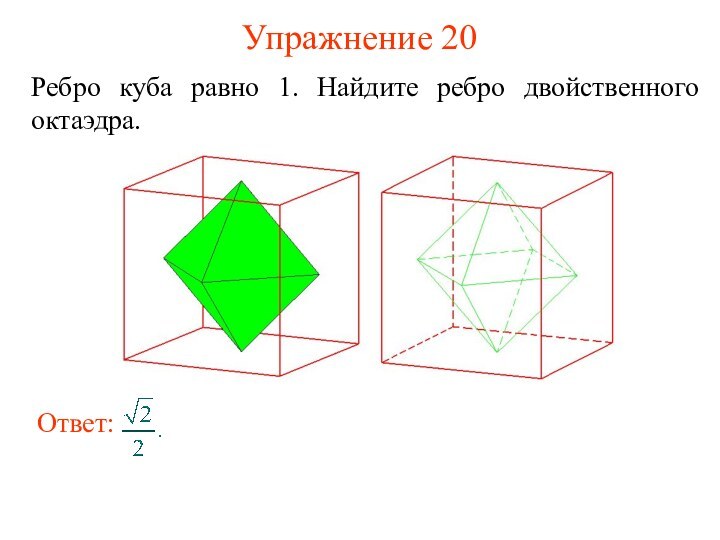
- 29. Упражнение 20Ребро куба равно 1. Найдите ребро двойственного октаэдра.
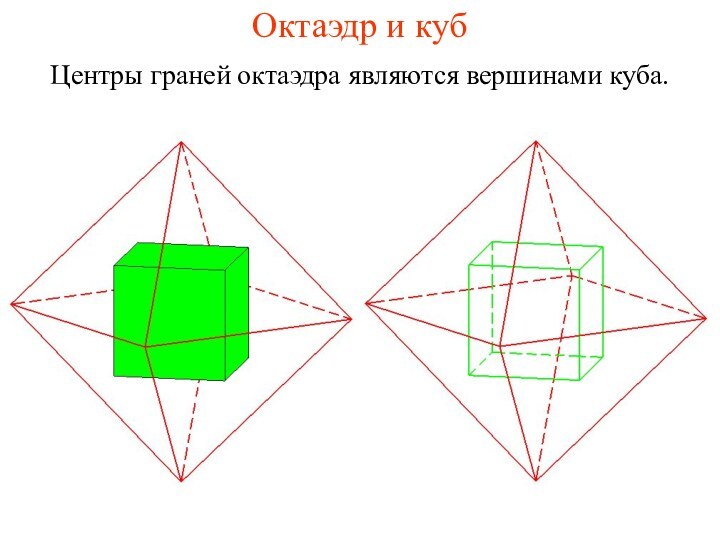
- 30. Октаэдр и кубЦентры граней октаэдра являются вершинами куба.
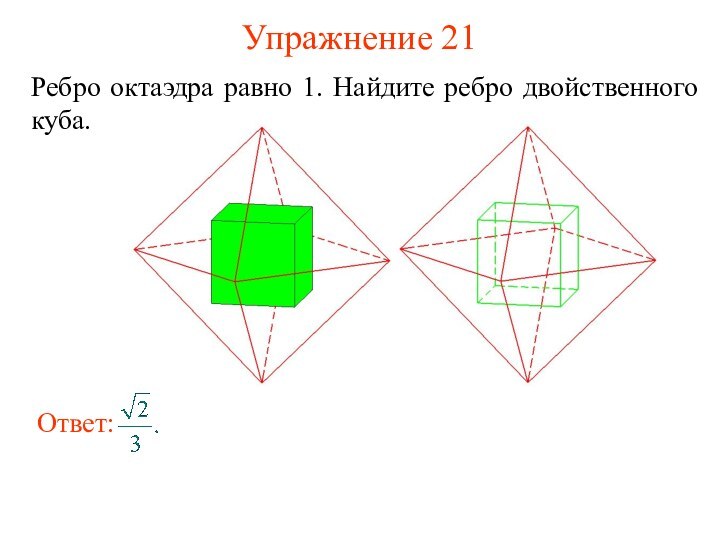
- 31. Упражнение 21Ребро октаэдра равно 1. Найдите ребро двойственного куба.
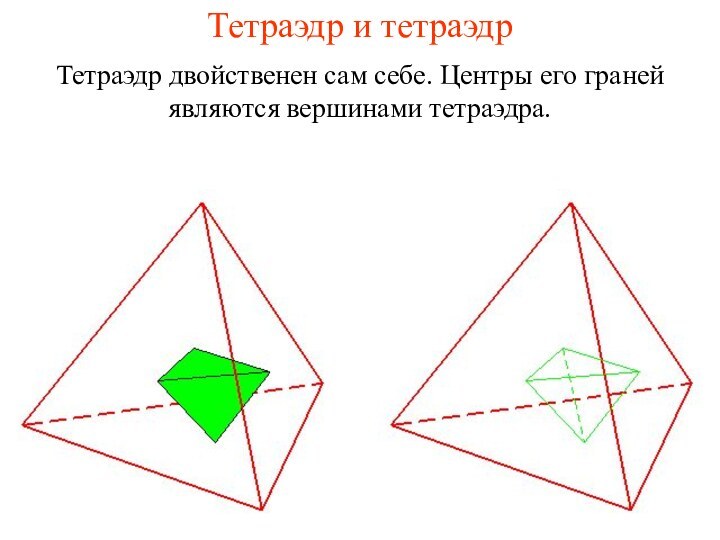
- 32. Тетраэдр и тетраэдрТетраэдр двойственен сам себе. Центры его граней являются вершинами тетраэдра.
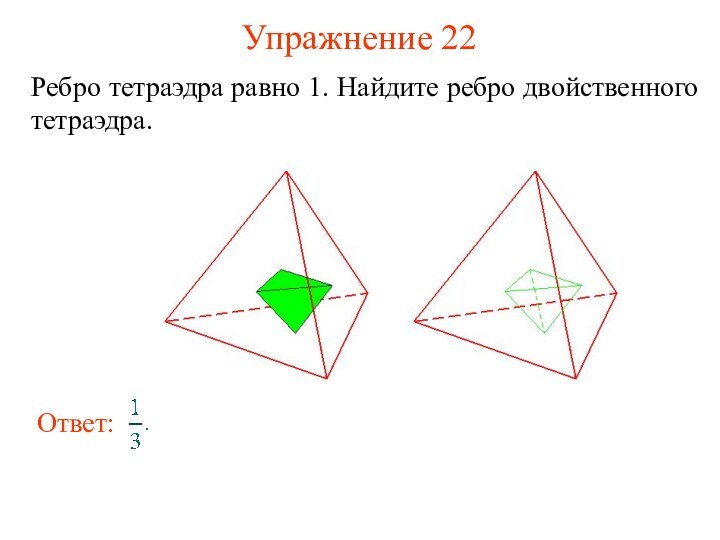
- 33. Упражнение 22Ребро тетраэдра равно 1. Найдите ребро двойственного тетраэдра.
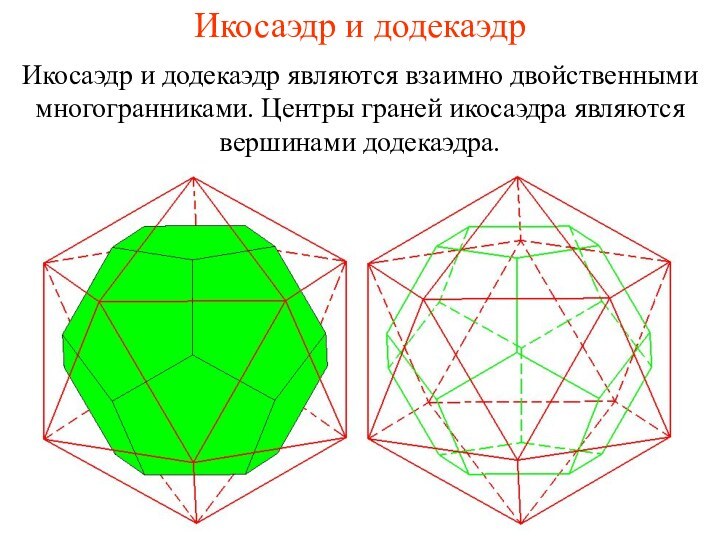
- 34. Икосаэдр и додекаэдрИкосаэдр и додекаэдр являются взаимно двойственными многогранниками. Центры граней икосаэдра являются вершинами додекаэдра.
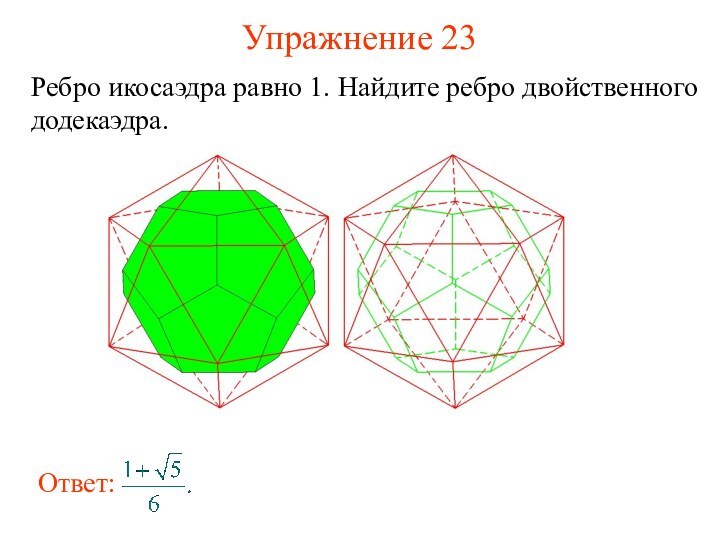
- 35. Упражнение 23Ребро икосаэдра равно 1. Найдите ребро двойственного додекаэдра.
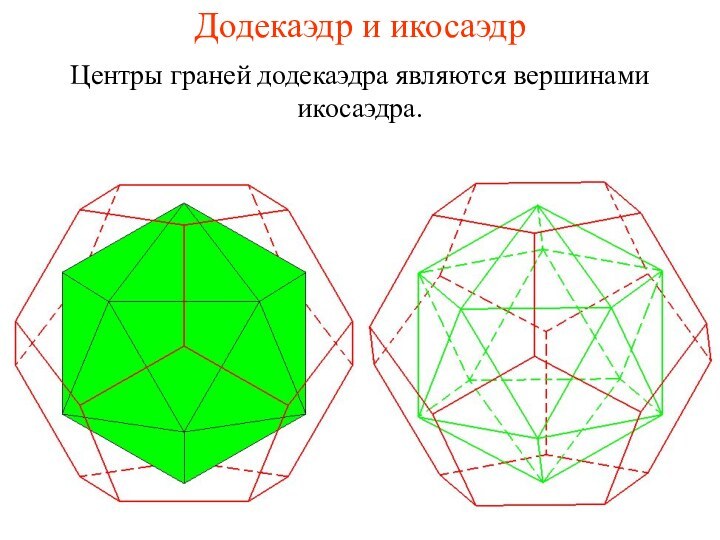
- 36. Додекаэдр и икосаэдрЦентры граней додекаэдра являются вершинами икосаэдра.
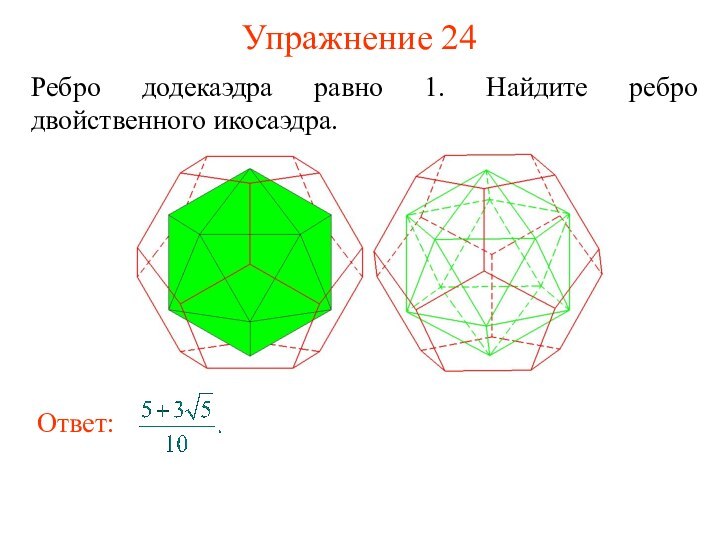
- 37. Упражнение 24Ребро додекаэдра равно 1. Найдите ребро двойственного икосаэдра.
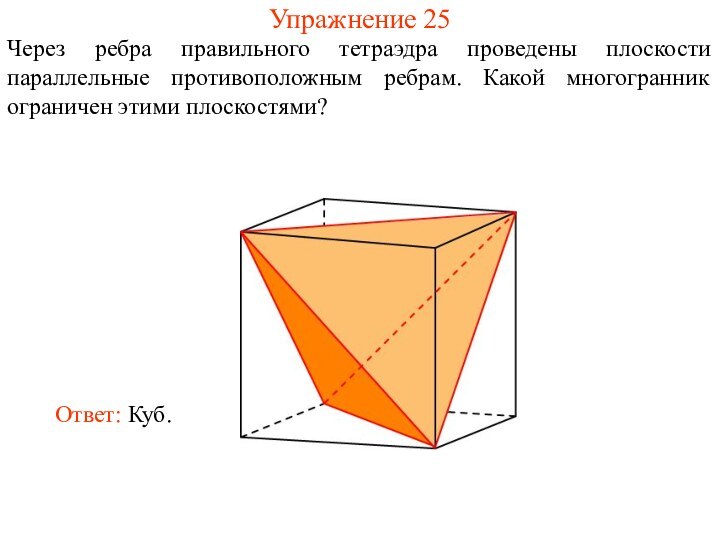
- 38. Упражнение 25Через ребра правильного тетраэдра проведены плоскости параллельные противоположным ребрам. Какой многогранник ограничен этими плоскостями?
- 39. Упражнение 26Через середины двух ребер куба, выходящих
- 40. Упражнение 27Через вершины куба, перпендикулярно его диагоналям,
- 41. Упражнение 28На рисунке изображен многогранник – звезда
- 42. Скачать презентацию
- 43. Похожие презентации
Кубок Кеплера Иоганн Кеплер (1571 – 1630) в одной из первых своих работ "Тайна мироздания" в 1596 году, используя правильные многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. Геометрия Солнечной системы, по







Слайд 3
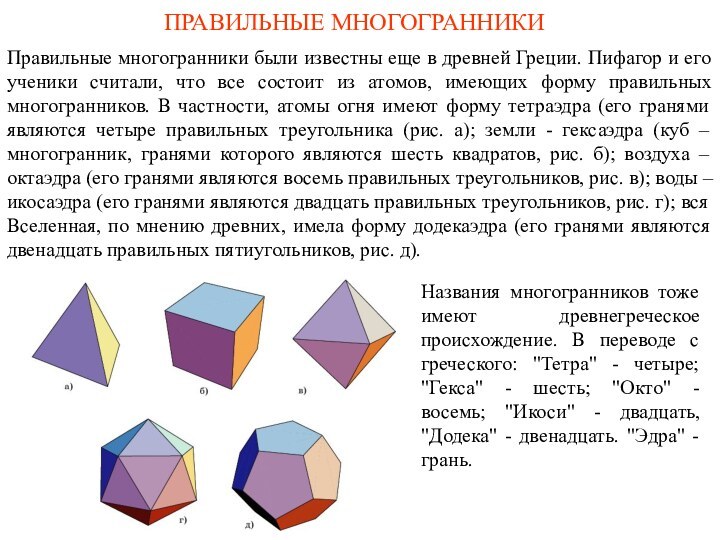
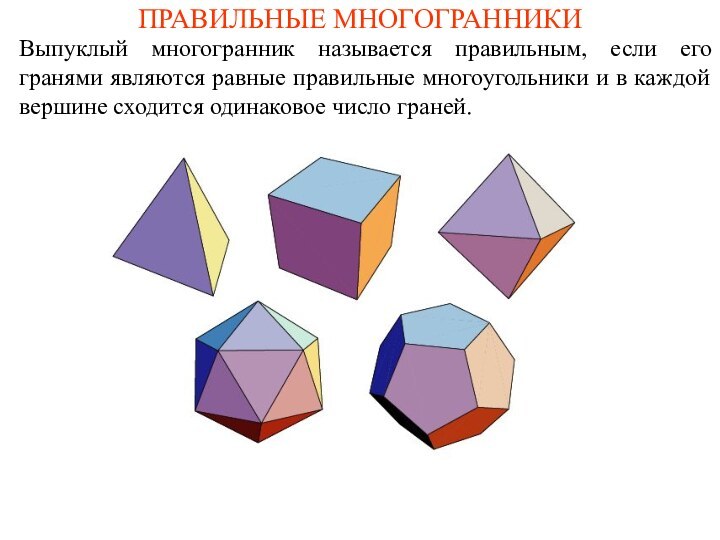
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Выпуклый многогранник называется правильным, если его гранями
являются равные правильные многоугольники и в каждой вершине сходится
одинаковое число граней.
Слайд 4
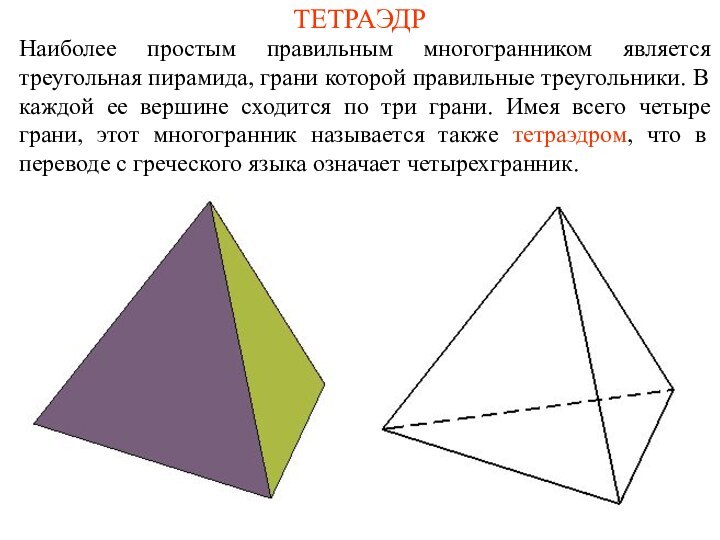
ТЕТРАЭДР
Наиболее простым правильным многогранником является треугольная пирамида, грани
которой правильные треугольники. В каждой ее вершине сходится по
три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.
Слайд 6
КУБ (ГЕКСАЭДР)
Многогранник, гранями которого являются квадраты и в
каждой вершине сходится три грани называется кубом или гексаэдром.
Слайд 8
ОКТАЭДР
Многогранник, гранями которого являются правильные треугольники и в
каждой вершине сходится четыре грани называется октаэдром.
Слайд 10
ИКОСАЭДР
Многогранник, в каждой вершине которого сходится пять правильных
треугольников называется икосаэдром.
Слайд 12
ДОДЕКАЭДР
Многогранник, гранями которого являются правильные пятиугольники и в
каждой вершине сходится три грани называется додекаэдром.
Слайд 14
Упражнение 6
Почему гранями правильного многогранника не могут быть
правильные шестиугольники?
Ответ: Потому что в этом случае сумма плоских
углов при вершинах будет больше или равна 360о.
Слайд 15
Упражнение 7
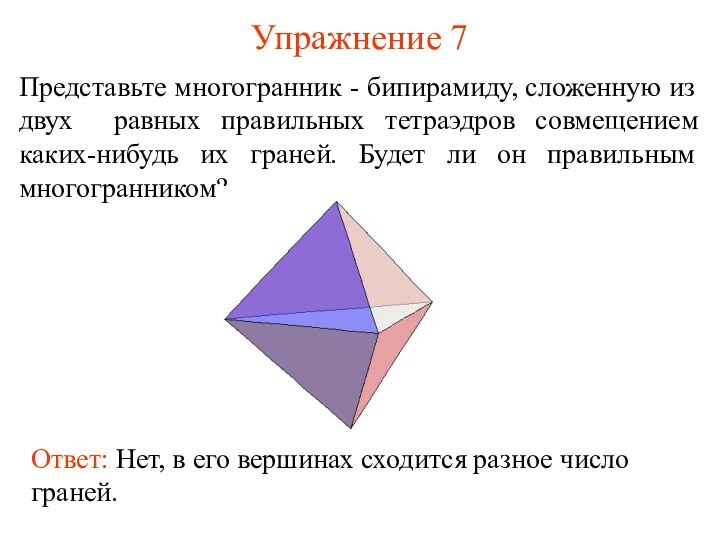
Представьте многогранник - бипирамиду, сложенную из двух
равных правильных тетраэдров совмещением каких-нибудь их граней. Будет ли
он правильным многогранником?Ответ: Нет, в его вершинах сходится разное число граней.
Слайд 20
Упражнение 12
Соединение каких двух многогранников изображено на рисунке?
Ответ:
Икосаэдра и додекаэдра.
Слайд 21
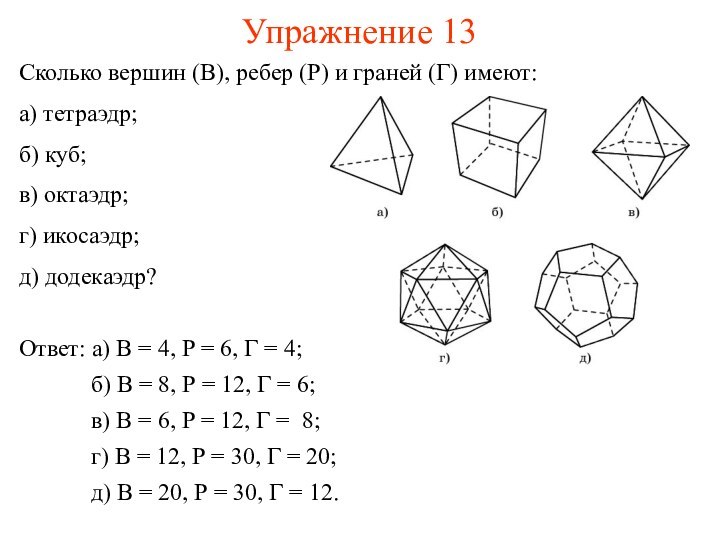
Упражнение 13
Сколько вершин (В), ребер (Р) и граней
(Г) имеют:
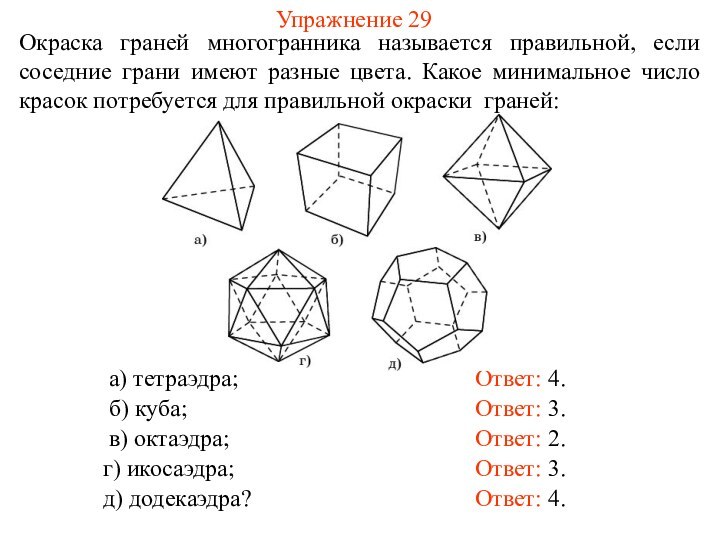
а) тетраэдр;
б) куб;
в) октаэдр;
г) икосаэдр;
д) додекаэдр?
Ответ: а) В
= 4, Р = 6, Г = 4;б) В = 8, Р = 12, Г = 6;
в) В = 6, Р = 12, Г = 8;
г) В = 12, Р = 30, Г = 20;
д) В = 20, Р = 30, Г = 12.
Слайд 28
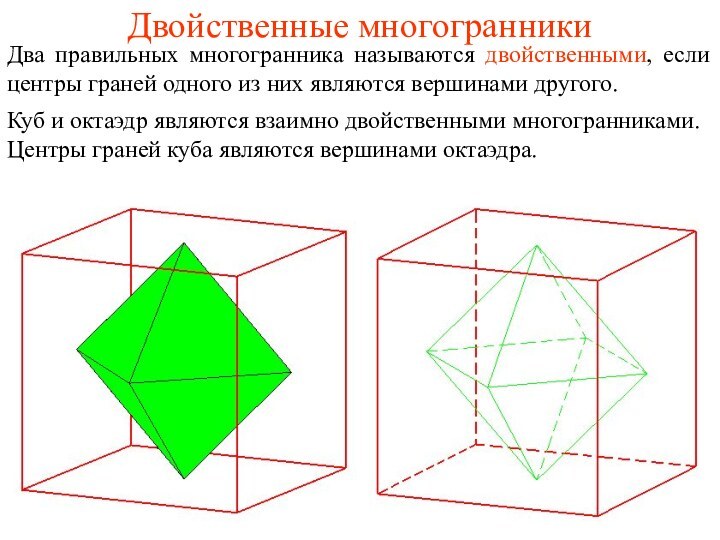
Двойственные многогранники
Два правильных многогранника называются двойственными, если центры
граней одного из них являются вершинами другого.
Куб и октаэдр
являются взаимно двойственными многогранниками. Центры граней куба являются вершинами октаэдра.
Слайд 32
Тетраэдр и тетраэдр
Тетраэдр двойственен сам себе. Центры его
граней являются вершинами тетраэдра.
Слайд 34
Икосаэдр и додекаэдр
Икосаэдр и додекаэдр являются взаимно двойственными
многогранниками. Центры граней икосаэдра являются вершинами додекаэдра.
Слайд 38
Упражнение 25
Через ребра правильного тетраэдра проведены плоскости параллельные
противоположным ребрам. Какой многогранник ограничен этими плоскостями?
Слайд 39
Упражнение 26
Через середины двух ребер куба, выходящих из
одной вершины, параллельно третьему ребру, выходящему из той же
вершины куба, проведено сечение, отсекающее от куба треугольную призму. Такие же сечения проведены через все возможные пары середин ребер, выходящих из вершин куба. Опишите многогранник, который останется от куба в результате этих отсечений. Сколько у него вершин, ребер и граней? Какую форму имеют грани? Нарисуйте этот многогранник.
Слайд 40
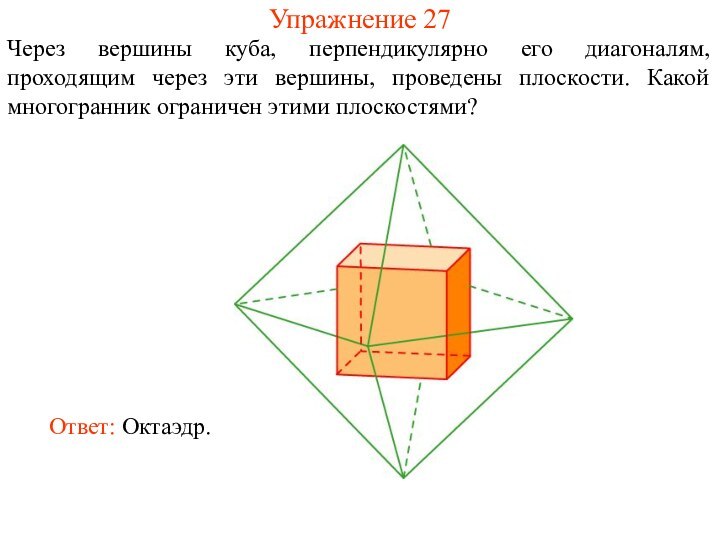
Упражнение 27
Через вершины куба, перпендикулярно его диагоналям, проходящим
через эти вершины, проведены плоскости. Какой многогранник ограничен этими
плоскостями?
Слайд 41
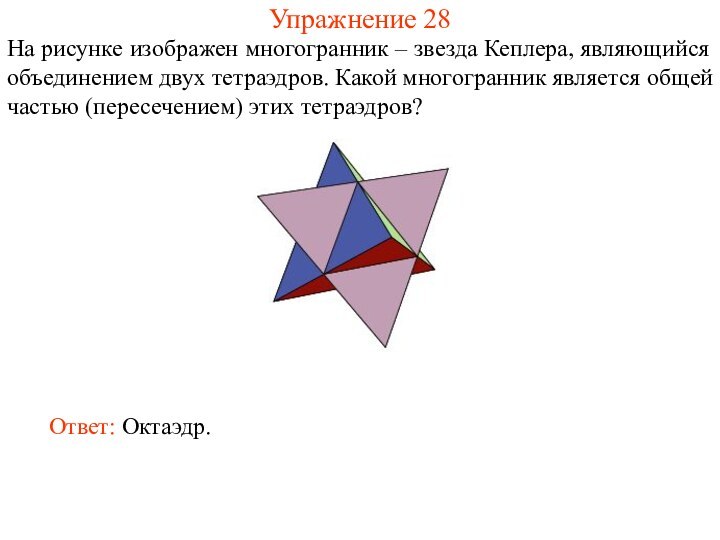
Упражнение 28
На рисунке изображен многогранник – звезда Кеплера,
являющийся объединением двух тетраэдров. Какой многогранник является общей частью
(пересечением) этих тетраэдров?Ответ: Октаэдр.