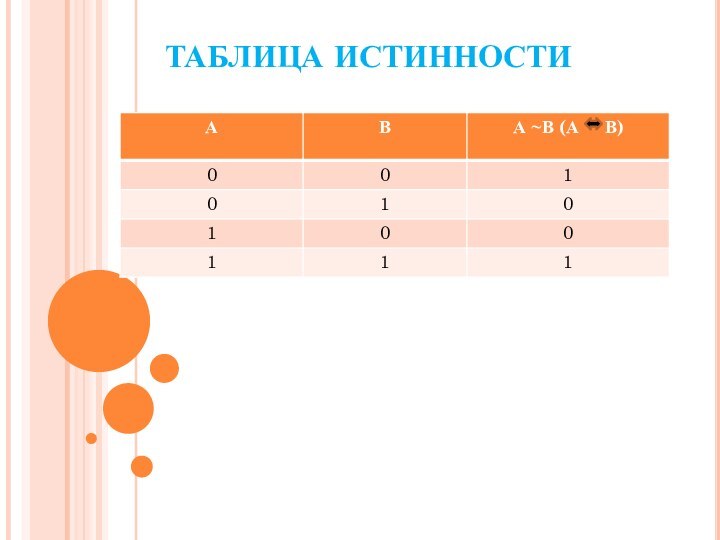
f(false), 0-ложное высказывание
- и(истина), t(true), 1-истинное высказывание
Например:
1.Сегодня 5 августа.
(ложное высказывание)2.В этом семестре студенты 2 курса факультета МИиФ изучают курс Дискретной математики. (истинное высказывание)