по два называют любую упорядоченную пару, составленную из данных n элементов.
Количество размещений из n элементов по два обозначают через (по первой букве французского слова arrangement – размещение)
Размещения
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






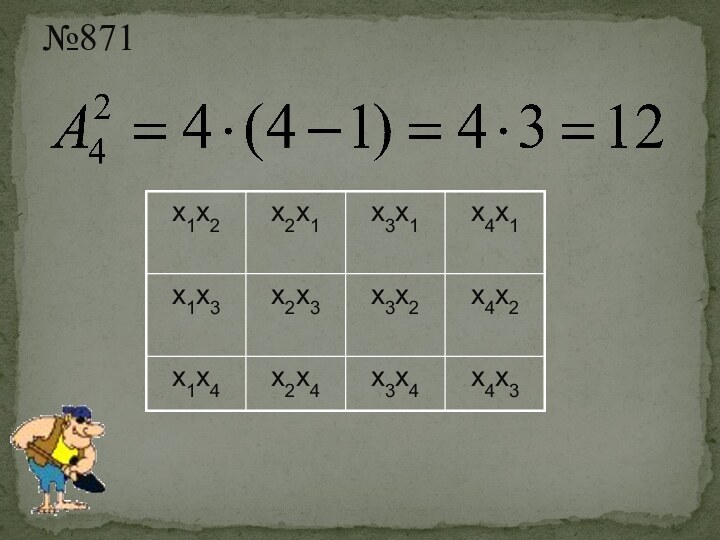

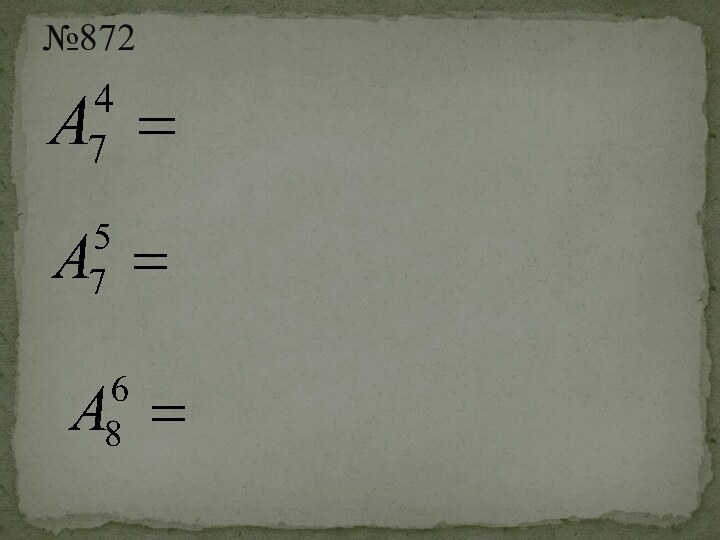





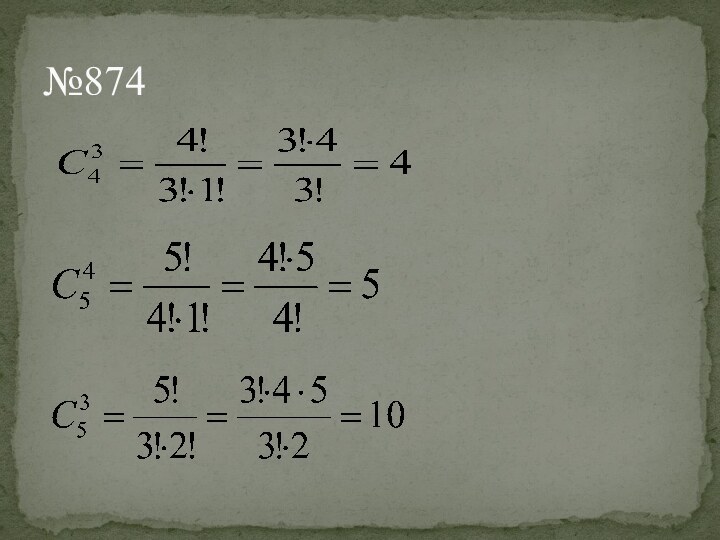



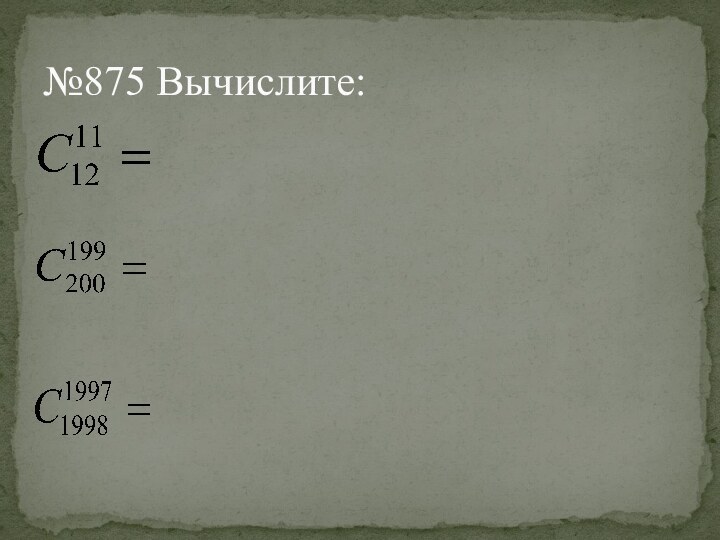






Размещения
Сочетания